Nomor 1
Tiga pria dan empat wanita akan duduk dalam satu baris. Banyak cara mereka duduk sehingga yang berjenis kelamin sama tidak berdampingan adalah ...
$\clubsuit \, $ Agar berjenis kelamin sama tidak berdampingan, maka susunan yang mungkin:
pada posisi pertama ada 4 pilihan wanita
pada posisi ketiga ada 3 pilihan wanita
pada posisi kelima ada 2 pilihan wanita
pada posisi ketujuh ada 1 pilihan wanita
pada posisi kedua ada 3 pilihan pria
pada posisi keempat ada 2 pilihan pria
pada posisi keenam ada 1 pilihan pria
dengan banyak cara :
$= 4.3.3.2.2.1.1 = 144 \, \,$ cara.
Jadi, total cara ada 144 susunan. $\heartsuit $
| W | P | W | P | W | P | W |
pada posisi ketiga ada 3 pilihan wanita
pada posisi kelima ada 2 pilihan wanita
pada posisi ketujuh ada 1 pilihan wanita
pada posisi kedua ada 3 pilihan pria
pada posisi keempat ada 2 pilihan pria
pada posisi keenam ada 1 pilihan pria
dengan banyak cara :
| 4 | 3 | 3 | 2 | 2 | 1 | 1 |
Jadi, total cara ada 144 susunan. $\heartsuit $
Nomor 2
Untuk setiap bilangan asli $n$ didefinisikan matriks $A_n = \left( \begin{matrix} n & 2n \\ 3n & 4n \end{matrix} \right) $ Jika $\text{det}(A_1+A_2+...+A_k)=-4050$ ,
maka $\text{det}(A_{2k})=...$
$A_n = \left( \begin{matrix} n & 2n \\ 3n & 4n \end{matrix} \right) \, $ , Misalkan :$p=1+2+3+...+k$
$\begin{align*} A_1+A_2+...+A_k&= \left( \begin{matrix} 1 & 2.1 \\ 3.1 & 4.1 \end{matrix} \right) + \left( \begin{matrix} 2 & 2.2 \\ 3.2 & 4.2 \end{matrix} \right) + ... + \left( \begin{matrix} k & 2.k \\ 3.k & 4.k \end{matrix} \right) \\ &= \left( \begin{matrix} (1+2+...+k) & 2(1+2+...+k) \\ 3(1+2+...+k) & 4(1+2+...+k) \end{matrix} \right)\\ &=\left( \begin{matrix} p & 2p \\ 3p & 4p \end{matrix} \right) \\ \text{det}(A_1+A_2+...+A_k)&=\text{det}\left( \begin{matrix} p & 2p \\ 3p & 4p \end{matrix} \right)=4p^2-6p^2=-2p^2\\ \text{det}(A_1+A_2+...+A_k)&=-4050\\ -2p^2&=-4050\\ p&=45 \end{align*}$
$\spadesuit \, $ Menentukan nilai $k$ :
$p=45 \, $ dan $S_n=\frac{n}{2}\left( u_1+u_n \right)$
$\begin{align*} p&=45 \\ 1+2+3+...+k &= 45\\ \frac{k}{2}\left( 1+k \right)&=45\\ k^2+k-9&=0\\ (k-9)(k+10)&=0\\ k=9 \, &\text{atau} \, k=-10\\ \text{yang memenuhi adalah } \, x&=9 \end{align*}$
$\spadesuit \, $ Menentukan nilai $\text{det}(A_{2k})$ :
$A_{2k}=A_{2.9}=A_18=\left( \begin{matrix} 18 & 2.18 \\ 3.18 & 4.18 \end{matrix} \right)$
$\text{det}(A_{2k})=\text{det}(A_{18})=\text{det}\left( \begin{matrix} 18 & 2.18 \\ 3.18 & 4.18 \end{matrix} \right)=-648$
Jadi determinan matriks $A_{2k}$ adalah -648 . $\heartsuit $
$\begin{align*} A_1+A_2+...+A_k&= \left( \begin{matrix} 1 & 2.1 \\ 3.1 & 4.1 \end{matrix} \right) + \left( \begin{matrix} 2 & 2.2 \\ 3.2 & 4.2 \end{matrix} \right) + ... + \left( \begin{matrix} k & 2.k \\ 3.k & 4.k \end{matrix} \right) \\ &= \left( \begin{matrix} (1+2+...+k) & 2(1+2+...+k) \\ 3(1+2+...+k) & 4(1+2+...+k) \end{matrix} \right)\\ &=\left( \begin{matrix} p & 2p \\ 3p & 4p \end{matrix} \right) \\ \text{det}(A_1+A_2+...+A_k)&=\text{det}\left( \begin{matrix} p & 2p \\ 3p & 4p \end{matrix} \right)=4p^2-6p^2=-2p^2\\ \text{det}(A_1+A_2+...+A_k)&=-4050\\ -2p^2&=-4050\\ p&=45 \end{align*}$
$\spadesuit \, $ Menentukan nilai $k$ :
$p=45 \, $ dan $S_n=\frac{n}{2}\left( u_1+u_n \right)$
$\begin{align*} p&=45 \\ 1+2+3+...+k &= 45\\ \frac{k}{2}\left( 1+k \right)&=45\\ k^2+k-9&=0\\ (k-9)(k+10)&=0\\ k=9 \, &\text{atau} \, k=-10\\ \text{yang memenuhi adalah } \, x&=9 \end{align*}$
$\spadesuit \, $ Menentukan nilai $\text{det}(A_{2k})$ :
$A_{2k}=A_{2.9}=A_18=\left( \begin{matrix} 18 & 2.18 \\ 3.18 & 4.18 \end{matrix} \right)$
$\text{det}(A_{2k})=\text{det}(A_{18})=\text{det}\left( \begin{matrix} 18 & 2.18 \\ 3.18 & 4.18 \end{matrix} \right)=-648$
Jadi determinan matriks $A_{2k}$ adalah -648 . $\heartsuit $
Nomor 3
Diketahui persamaan $x^2+px+q=0$ mempunyai akar-akar positif $x_1$ dan $x_2$ . Jika $x_1$ , $6$, $x_2$ adalah tiga suku pertama barisan
geometri dan $x_1$ , $x_2$ , $14$ tiga suku pertama barisan aritmatika, maka $p+q=...$
$x^2+px+q=0 \,$ memiliki akar-akar positif $x_1$ dan $x_2$
$x_1+x_2=\frac{-b}{a} \Rightarrow x_1+x_2=\frac{-p}{1}=-p \,$ pers(i)
$x_1.x_2=\frac{c}{a} \Rightarrow x_1.x_2=\frac{q}{1}=q \, $ pers(ii)
$\clubsuit \, x_1 , 6, x_2 \, $ barisan geometri (rasionya sama) :
$\frac{6}{x_1}=\frac{x_2}{6} \Leftrightarrow x_1.x_2=36 \, \text{pers (iii)} \Leftrightarrow q=36$
$\clubsuit \, x_1 , x_2 , 14 \, $ barisan aritmatika (bedanya sama) :
$x_2-x_1=14-x_2 \Leftrightarrow x_1=2x_2-14 \, \text{pers (iv)}$
$\clubsuit \, $ Substitusikan pers(iv) ke pers(iii) :
$\begin{align*} x_1.x_2&=36 \\ (2x_2-14)x_2&=36 \\ x_2^2-7x_2-18&=0\\ (x_2-9)(x_2+2)&=0\\ x_2=9 \, &\text{atau} \, x_2=-2\\ \text{yang memenuhi adalah } \, x_2&=9 \end{align*}$
pers(iv) : $x_1=2x_2-14 \Leftrightarrow x_1=2.9-14 \Leftrightarrow x_1=4 $
pers(i) : $x_1+x_2=-p \Leftrightarrow 4 + 9 =-p \Leftrightarrow p=-13$
Jadi, nilai $p+q=-13+36=23 . \heartsuit $
$x_1+x_2=\frac{-b}{a} \Rightarrow x_1+x_2=\frac{-p}{1}=-p \,$ pers(i)
$x_1.x_2=\frac{c}{a} \Rightarrow x_1.x_2=\frac{q}{1}=q \, $ pers(ii)
$\clubsuit \, x_1 , 6, x_2 \, $ barisan geometri (rasionya sama) :
$\frac{6}{x_1}=\frac{x_2}{6} \Leftrightarrow x_1.x_2=36 \, \text{pers (iii)} \Leftrightarrow q=36$
$\clubsuit \, x_1 , x_2 , 14 \, $ barisan aritmatika (bedanya sama) :
$x_2-x_1=14-x_2 \Leftrightarrow x_1=2x_2-14 \, \text{pers (iv)}$
$\clubsuit \, $ Substitusikan pers(iv) ke pers(iii) :
$\begin{align*} x_1.x_2&=36 \\ (2x_2-14)x_2&=36 \\ x_2^2-7x_2-18&=0\\ (x_2-9)(x_2+2)&=0\\ x_2=9 \, &\text{atau} \, x_2=-2\\ \text{yang memenuhi adalah } \, x_2&=9 \end{align*}$
pers(iv) : $x_1=2x_2-14 \Leftrightarrow x_1=2.9-14 \Leftrightarrow x_1=4 $
pers(i) : $x_1+x_2=-p \Leftrightarrow 4 + 9 =-p \Leftrightarrow p=-13$
Jadi, nilai $p+q=-13+36=23 . \heartsuit $
Nomor 4
Jika $f(x)=(sinx+cosx)(cos2x+sin2x)$ dan $f^\prime (x)=2cos3x + g(x)$ maka $g(x)=...$
$\spadesuit \, $ Rumus perkalian:
$sinxcosy=\frac{1}{2}(sin(x+y)+sin(x-y)) , cosxsiny=\frac{1}{2}(sin(x+y)-sin(x-y)), \\ sinxsiny=-\frac{1}{2}(cos(x+y)-cos(x-y)) , cosxcosy=\frac{1}{2}(cos(x+y)+cos(x-y)) $
$\spadesuit \, $ Menyederhanakan fungsi $f(x)$:
$\begin{align*} f(x)&=(sinx+cosx)(cos2x+sin2x)\\ &=cos2xsinx+sin2xsinx+cos2xcosx+sin2xcox \\ &=\frac{1}{2}(sin3x-sinx) -\frac{1}{2}(cos3x-cosx)\\ &\, +\frac{1}{2}(cos3x+cosx)+\frac{1}{2}(sin3x+sinx)\\ f(x)&=sin3x+cosx\\ f^\prime (x)&=3cos3x-sinx \end{align*}$
$\spadesuit \, $ Menentukan fungsi $g(x)$:
$\begin{align*} f^\prime (x)&=2cos3x + g(x)\\ g(x)&=f^\prime (x)-2cos3x\\ g(x)&=(3cos3x-sinx)-2cos3x\\ g(x)&=cos3x-sinx \end{align*}$
Jadi, Nilai $ g(x)=cos3x-sinx \, \heartsuit $
$sinxcosy=\frac{1}{2}(sin(x+y)+sin(x-y)) , cosxsiny=\frac{1}{2}(sin(x+y)-sin(x-y)), \\ sinxsiny=-\frac{1}{2}(cos(x+y)-cos(x-y)) , cosxcosy=\frac{1}{2}(cos(x+y)+cos(x-y)) $
$\spadesuit \, $ Menyederhanakan fungsi $f(x)$:
$\begin{align*} f(x)&=(sinx+cosx)(cos2x+sin2x)\\ &=cos2xsinx+sin2xsinx+cos2xcosx+sin2xcox \\ &=\frac{1}{2}(sin3x-sinx) -\frac{1}{2}(cos3x-cosx)\\ &\, +\frac{1}{2}(cos3x+cosx)+\frac{1}{2}(sin3x+sinx)\\ f(x)&=sin3x+cosx\\ f^\prime (x)&=3cos3x-sinx \end{align*}$
$\spadesuit \, $ Menentukan fungsi $g(x)$:
$\begin{align*} f^\prime (x)&=2cos3x + g(x)\\ g(x)&=f^\prime (x)-2cos3x\\ g(x)&=(3cos3x-sinx)-2cos3x\\ g(x)&=cos3x-sinx \end{align*}$
Jadi, Nilai $ g(x)=cos3x-sinx \, \heartsuit $
Nomor 5
Diketahui $D_1$ adalah daerah di kuadran I yang dibatasi oleh parabola $y=\frac{9}{4}x^2$ , parabola $y=x^2$ , dan
garis $x=2$ , dan $D_2$ daerah yang dibatasi oleh garis $x=2$ , garis $y=9$ ,
dan parabola $y=x^2$ . Jika luas $D_1=a$ , maka luas $D_2$ adalah ...
$\clubsuit \, $ Luas $D_1$ : $(L_{D_1} = a)$
$\begin{align*} L_{D_1} &= \int_0^2\left( \frac{9}{4}x^2 - x^2 \right) \\ &= \int_0^2\left( \frac{5}{4}x^2 \right) =\frac{10}{3} \\ L_{D_1} &= a \Leftrightarrow a = \frac{10}{3}\\ \end{align*}$
$\clubsuit \, $ Luas $D_2$ :
$\begin{align*} L_{D_2} &= \int_2^3\left( 9 - x^2 \right)=\frac{8}{3} \end{align*}$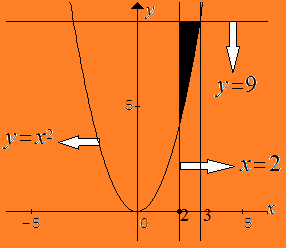
Sehingga $L_{D_2}=\frac{8}{3} . \frac{10}{10} = \frac{8}{10} . \frac{10}{3} = \frac{8}{10} a .$
Jadi, $L_{D_2}=\frac{8}{10} a \, \heartsuit $
$\begin{align*} L_{D_1} &= \int_0^2\left( \frac{9}{4}x^2 - x^2 \right) \\ &= \int_0^2\left( \frac{5}{4}x^2 \right) =\frac{10}{3} \\ L_{D_1} &= a \Leftrightarrow a = \frac{10}{3}\\ \end{align*}$

$\clubsuit \, $ Luas $D_2$ :
$\begin{align*} L_{D_2} &= \int_2^3\left( 9 - x^2 \right)=\frac{8}{3} \end{align*}$

Sehingga $L_{D_2}=\frac{8}{3} . \frac{10}{10} = \frac{8}{10} . \frac{10}{3} = \frac{8}{10} a .$
Jadi, $L_{D_2}=\frac{8}{10} a \, \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.