Nomor 11
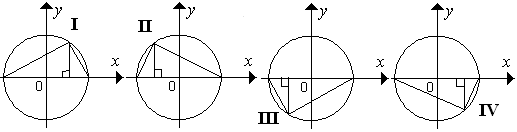
Vektor $\vec{x} $ dicerminkan terhadap garis $y=0 $ . Kemudian hasilnya diputar terhadap titik asal O sebesar $\theta $ > 0
searah jarum jam, menghasilkan vektor $\vec{y} $ . Jika $\vec{y} = A\vec{x} $ , maka matriks $A = ...$
$\clubsuit \, $ Menentukan matriks transformasinya :
* Pertama, dicerminkan terhadap garis $y=0 $ (sumbu X )
T$_1=\left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
** Kedua, dirotasi dengan pusat (0,0) sebesar $\theta $ searah jarum jam ($\theta $ negatif )
T$_2=\left( \begin{matrix} \cos (-\theta ) & -\sin (-\theta ) \\ \sin (-\theta ) & \cos (-\theta ) \end{matrix} \right) =\left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) $
Ingat : $\cos (-x) = \cos x $ dan $\sin (-x) = -\sin x $
$\clubsuit \, $ Matriks gabungannya (MT) :
MT = T$_2$ . T$_1$ = $ \left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
$\vec{y} = A\vec{x} $ artinya A adalah matriks gabungannya, sehingga A = MT
Jadi, nilai $A = \left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) . \heartsuit $
* Pertama, dicerminkan terhadap garis $y=0 $ (sumbu X )
T$_1=\left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
** Kedua, dirotasi dengan pusat (0,0) sebesar $\theta $ searah jarum jam ($\theta $ negatif )
T$_2=\left( \begin{matrix} \cos (-\theta ) & -\sin (-\theta ) \\ \sin (-\theta ) & \cos (-\theta ) \end{matrix} \right) =\left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) $
Ingat : $\cos (-x) = \cos x $ dan $\sin (-x) = -\sin x $
$\clubsuit \, $ Matriks gabungannya (MT) :
MT = T$_2$ . T$_1$ = $ \left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
$\vec{y} = A\vec{x} $ artinya A adalah matriks gabungannya, sehingga A = MT
Jadi, nilai $A = \left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix} \right) \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) . \heartsuit $
Nomor 12
Himpunan $A $ memenuhi hubungan $\{1\} \subset A \subset \{1,2,3,4,5,6\} $ . Jika 6 adalah anggota $A $ , maka banyak himpunan
$A $ yang mungkin adalah ...
$\spadesuit \, $ Karena 1 adalah himpunan bagian dari A ($\{1\} \subset A$ ), maka A harus memuat angka 1
Dari soal, A juga sudah memuat angka 6, artinya A sudah memuat 2 anggota yaitu 1 dan 6. Sehingga angka yang bisa dipilih tinggal angka-angka 2,3,4, dan 5.
$\spadesuit \, $ Banyakknya himpunan A berdasarkan banyak anggotanya :
* 2 anggota ada 1 himpunan
* 3 anggota ada $C_1^4 = 4 $ himpunan, maksudnya A telah memuat 1 dan 6 sehingga satu anggota lagi dipilih dari angka-angka 2,3,4,5 yaitu menggunakan kombinasi 1 dari 4.
* 4 anggota ada $C_2^4 = 6 $ himpunan
* 5 anggota ada $C_3^4 = 4 $ himpunan
* 6 anggota ada $C_4^4 = 1 $ himpunan
total himpunan = 1 + 4 + 6 + 4 + 1 = 16 himpunan.
Jadi, banyak himpunan A yang mungkin ada 16 himpunan. $ \heartsuit $
Dari soal, A juga sudah memuat angka 6, artinya A sudah memuat 2 anggota yaitu 1 dan 6. Sehingga angka yang bisa dipilih tinggal angka-angka 2,3,4, dan 5.
$\spadesuit \, $ Banyakknya himpunan A berdasarkan banyak anggotanya :
* 2 anggota ada 1 himpunan
* 3 anggota ada $C_1^4 = 4 $ himpunan, maksudnya A telah memuat 1 dan 6 sehingga satu anggota lagi dipilih dari angka-angka 2,3,4,5 yaitu menggunakan kombinasi 1 dari 4.
* 4 anggota ada $C_2^4 = 6 $ himpunan
* 5 anggota ada $C_3^4 = 4 $ himpunan
* 6 anggota ada $C_4^4 = 1 $ himpunan
total himpunan = 1 + 4 + 6 + 4 + 1 = 16 himpunan.
Jadi, banyak himpunan A yang mungkin ada 16 himpunan. $ \heartsuit $
Nomor 13
Diketahui suku banyak $p(x) = x^2+bx+c $ . Jika $b $ dan $c $ dipilih secara acak dari selang [0,2], maka peluang suku
banyak tersebut tidak mempunyai akar adalah ...
$\spadesuit \, $ Karena $b$ dan $c$ dipilih pada selang [0,2] artinya nilai $0 \leq b \leq 2$
dan $0 \leq c \leq 2 $ , yang mana ada tak hingga banyaknya angka,
maka nilai $n(A) $ dan $n(S) $ diwakili oleh luasan.

$n(S) = \text{Luas Persegi} = 2\times 2 = 4 $
$\spadesuit \, $ Agar $p(x) = x^2+bx+c \, \, $ tidak punya akar, maka nilai $ D < 0 $
$\begin{align} D < 0 \rightarrow b^2 - 4ac & < 0 \\ b^2 - 4.1.c & < 0 \\ b^2 - 4c & < 0 \end{align}$
Artinya nilai $b$ dan $c$ pada selang [0,2] harus memenuhi $ b^2 - 4c < 0 $
$\spadesuit \, $ gambar $ b^2 - 4c = 0 \rightarrow c = \frac{b^2}{4} $
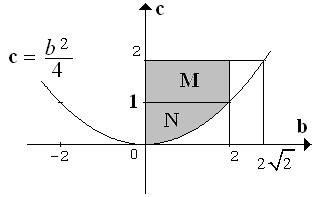
$\spadesuit \, $ Cek titik (b,c) = (0,1) ke $ b^2 - 4c < 0 $
$\begin{align} b^2 - 4c & < 0 \\ 0^2-4\times 1 & < 0 \\ -4 & < 0 \, \, \, \text{(benar)} \end{align}$
Artinya daerah yang memenuhi $ b^2 - 4c < 0 \, \, $ ada di dalam parabola seperti pada gambar di atas dan ada dalam selang [0,2] .
$\spadesuit \, $ Daerah yang diarsir (M dan N ) merupakan nilai $b$ dan $c$ agar $P(x)$ tidak punya akar.
Luas M = 2 . 1 = 2
Luas N = $\frac{2}{3}. \text{Luas persegi panjang} = \frac{2}{3} . 2 . 1 = \frac{4}{3} $
sehingga : $n(A) = $ Luas M + Luas N = 2 + $ \frac{4}{3} = \frac{10}{3}$
$P(A) = \frac{n(A)}{n(S)} = \frac{\frac{10}{3}}{4}= \frac{5}{6} $
Jadi, peluangnya adalah $ \frac{5}{6} . \heartsuit $

$n(S) = \text{Luas Persegi} = 2\times 2 = 4 $
$\spadesuit \, $ Agar $p(x) = x^2+bx+c \, \, $ tidak punya akar, maka nilai $ D < 0 $
$\begin{align} D < 0 \rightarrow b^2 - 4ac & < 0 \\ b^2 - 4.1.c & < 0 \\ b^2 - 4c & < 0 \end{align}$
Artinya nilai $b$ dan $c$ pada selang [0,2] harus memenuhi $ b^2 - 4c < 0 $
$\spadesuit \, $ gambar $ b^2 - 4c = 0 \rightarrow c = \frac{b^2}{4} $

$\spadesuit \, $ Cek titik (b,c) = (0,1) ke $ b^2 - 4c < 0 $
$\begin{align} b^2 - 4c & < 0 \\ 0^2-4\times 1 & < 0 \\ -4 & < 0 \, \, \, \text{(benar)} \end{align}$
Artinya daerah yang memenuhi $ b^2 - 4c < 0 \, \, $ ada di dalam parabola seperti pada gambar di atas dan ada dalam selang [0,2] .
$\spadesuit \, $ Daerah yang diarsir (M dan N ) merupakan nilai $b$ dan $c$ agar $P(x)$ tidak punya akar.
Luas M = 2 . 1 = 2
Luas N = $\frac{2}{3}. \text{Luas persegi panjang} = \frac{2}{3} . 2 . 1 = \frac{4}{3} $
sehingga : $n(A) = $ Luas M + Luas N = 2 + $ \frac{4}{3} = \frac{10}{3}$
$P(A) = \frac{n(A)}{n(S)} = \frac{\frac{10}{3}}{4}= \frac{5}{6} $
Jadi, peluangnya adalah $ \frac{5}{6} . \heartsuit $
Nomor 14
Nilai $\sqrt{3} \sin x - \cos x < 0 $ , jika ...
$\spadesuit \, $ Menyederhanakan soal :
$\begin{align*} \sqrt{3} \sin x - \cos x & < 0 \\ \sqrt{3} \sin x < \cos x \\ \frac{\sin x }{\cos x } & < \frac{1}{\sqrt{3}} \\ \tan x & < \frac{1}{3} \sqrt{3} \\ \tan x & = \tan \frac{\pi}{6} \end{align*}$
$\spadesuit \, $ Konsep dasar : $\tan x = \tan \theta \rightarrow x = \theta + k.\pi$
$\begin{align*} x & = \frac{\pi}{6} + k\pi \\ k=0 \rightarrow x & = \frac{\pi}{6} + 0.\pi = \frac{\pi}{6} \\ k=1 \rightarrow x & = \frac{\pi}{6} + 1.\pi = \frac{7\pi}{6} \\ k=2 \rightarrow x & = \frac{\pi}{6} + 2.\pi = \frac{13\pi}{6} \end{align*}$

Bentuk ketaksamaannya $< $ , sehingga yang diarsir yang bertanda negatif.
Dari opsi, yang memenuhi selang bertanda negatif di atas adalah $\frac{7\pi}{6} < x < \frac{11\pi}{7} \, $ .
Jadi, solusinya adalah HP = $ \frac{7\pi}{6} < x < \frac{11\pi}{7} . \heartsuit $
$\begin{align*} \sqrt{3} \sin x - \cos x & < 0 \\ \sqrt{3} \sin x < \cos x \\ \frac{\sin x }{\cos x } & < \frac{1}{\sqrt{3}} \\ \tan x & < \frac{1}{3} \sqrt{3} \\ \tan x & = \tan \frac{\pi}{6} \end{align*}$
$\spadesuit \, $ Konsep dasar : $\tan x = \tan \theta \rightarrow x = \theta + k.\pi$
$\begin{align*} x & = \frac{\pi}{6} + k\pi \\ k=0 \rightarrow x & = \frac{\pi}{6} + 0.\pi = \frac{\pi}{6} \\ k=1 \rightarrow x & = \frac{\pi}{6} + 1.\pi = \frac{7\pi}{6} \\ k=2 \rightarrow x & = \frac{\pi}{6} + 2.\pi = \frac{13\pi}{6} \end{align*}$

Bentuk ketaksamaannya $< $ , sehingga yang diarsir yang bertanda negatif.
Dari opsi, yang memenuhi selang bertanda negatif di atas adalah $\frac{7\pi}{6} < x < \frac{11\pi}{7} \, $ .
Jadi, solusinya adalah HP = $ \frac{7\pi}{6} < x < \frac{11\pi}{7} . \heartsuit $
Cara II : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=\pi \Rightarrow \sqrt{3} \sin x - \cos x & < 0 \\ \sqrt{3} \sin \pi - \cos \pi & < 0 \\ \sqrt{3} . 0 - (-1) & < 0 \\ 1 & < 0 \, \, \text{(salah)} \end{align*}$
yang ada $x=\pi$ salah, opsi yang salah adalah B, C, D, dan E.
Jadi, opsi yang benar adalah A yaitu HP = $ \frac{7\pi}{6} < x < \frac{11\pi}{7} . \heartsuit $
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=\pi \Rightarrow \sqrt{3} \sin x - \cos x & < 0 \\ \sqrt{3} \sin \pi - \cos \pi & < 0 \\ \sqrt{3} . 0 - (-1) & < 0 \\ 1 & < 0 \, \, \text{(salah)} \end{align*}$
yang ada $x=\pi$ salah, opsi yang salah adalah B, C, D, dan E.
Jadi, opsi yang benar adalah A yaitu HP = $ \frac{7\pi}{6} < x < \frac{11\pi}{7} . \heartsuit $
Nomor 15
Diketahui $|\vec{u}|=1 $ dan $|\vec{v}|=2 $ . Jika $\vec{u} $ dan $\vec{v} $ membentuk sudut 30$^o $ , maka ($\vec{u}+\vec{v} ) . \vec{v} = ...$
$\clubsuit \, $ Rumus dasar :
$\vec{u} . \vec{v} = |\vec{u}|\times |\vec{v}| \cos \theta \, \, \, $ dan $\, \, \, \vec{v} . \vec{v} = |\vec{v}|^2 $
$\begin{align*} (\vec{u}+\vec{v} ) . \vec{v} & = \vec{u} . \vec{v} + \vec{v} . \vec{v} \\ & = |\vec{u}|\times |\vec{v}| \cos \theta + |\vec{v}|^2 \\ & = 1 \times 2 \times \cos 30^o + (2)^2 \\ & = 2 \times \frac{1}{2} \sqrt{3} + 4 \\ & = \sqrt{3} + 4 \end{align*}$
Jadi, nilai $ (\vec{u}+\vec{v} ) . \vec{v} = \sqrt{3} + 4 . \heartsuit $
$\begin{align*} (\vec{u}+\vec{v} ) . \vec{v} & = \vec{u} . \vec{v} + \vec{v} . \vec{v} \\ & = |\vec{u}|\times |\vec{v}| \cos \theta + |\vec{v}|^2 \\ & = 1 \times 2 \times \cos 30^o + (2)^2 \\ & = 2 \times \frac{1}{2} \sqrt{3} + 4 \\ & = \sqrt{3} + 4 \end{align*}$
Jadi, nilai $ (\vec{u}+\vec{v} ) . \vec{v} = \sqrt{3} + 4 . \heartsuit $