Hallow sobat, bagaimana kabarnya hari ini? Semoga baik-baik saja.
Pembahasan Soal SPMB Matematika IPA tahun 2007 nomor 1 sampai nomor 5 menurut kami cukup menantang terutama untuk nomor 3 yang menggunakan konsep limit dan nomor 5 tentang pertidaksamaan trigonometri yang jawabannya cukup panjang. Nah untuk pembahasan nomor 2 itu tentang turunan sekaligus barisan dan deret geometri tak hingga, agak merepotkan karena melibatkan dua teori sekaligus. Sebenarnya yang sulit juga nomor 1 tentang dimensi tiga, biasa kalau dimensi tiga pasti menyulitkan, tapi tenang, kami menyertakan dua alternatif pembahasannya. Dan yang menurut kami mudah adalah soal nomor 4, karena menggunakan teori matriks, hanya saja harus penuh dengan ketelitian dalam perhitungannya karena melibatkan banyak angka.
Untuk penjelasan lebih lengkap mengenai Pembahasan Soal SPMB Matematika IPA tahun 2007, langsung saja simak penjelsannya berikut untuk nomor 1 sampai nomor 5. Selamat belajar.
Nomor 1
Diketahui kubus ABCD.EFGH yang mempunyai panjang rusuk 1 cm. Jarak D ke bidang EBG sama dengan ....
$\clubsuit \, $ Gambar
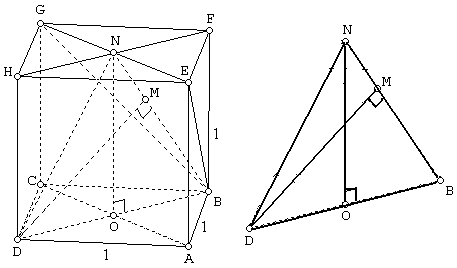
Jarak (D,EBG) = panjang DM pada segitiga DBN
$\clubsuit \, $ Menentukan panjang BN
$\Delta BNF, \, BN = \sqrt{BF^2+FN^2} = \sqrt{1^2+(\frac{1}{2}\sqrt{2})^2} = \frac{1}{2}\sqrt{6} $
$\clubsuit \, $ Menentukan panjang DM dengan luas segitiga DBN
$\begin{align} \text{Luas DBN (alas BN)} & = \text{Luas DBN (alas DB)} \\ \frac{1}{2}.BN.DM & = \frac{1}{2}.DB.NO \\ BN.DM & = DB.NO \\ DM & = \frac{DB.NO}{BN} = \frac{\sqrt{2}. 1}{\frac{1}{2}\sqrt{6}} = \frac{2}{3}\sqrt{3} \end{align}$
Jadi, jarak D ke bidang EBG adalah $ \frac{2}{3}\sqrt{3} . \heartsuit $

Jarak (D,EBG) = panjang DM pada segitiga DBN
$\clubsuit \, $ Menentukan panjang BN
$\Delta BNF, \, BN = \sqrt{BF^2+FN^2} = \sqrt{1^2+(\frac{1}{2}\sqrt{2})^2} = \frac{1}{2}\sqrt{6} $
$\clubsuit \, $ Menentukan panjang DM dengan luas segitiga DBN
$\begin{align} \text{Luas DBN (alas BN)} & = \text{Luas DBN (alas DB)} \\ \frac{1}{2}.BN.DM & = \frac{1}{2}.DB.NO \\ BN.DM & = DB.NO \\ DM & = \frac{DB.NO}{BN} = \frac{\sqrt{2}. 1}{\frac{1}{2}\sqrt{6}} = \frac{2}{3}\sqrt{3} \end{align}$
Jadi, jarak D ke bidang EBG adalah $ \frac{2}{3}\sqrt{3} . \heartsuit $
Cara II
$\clubsuit \, $ Gambar
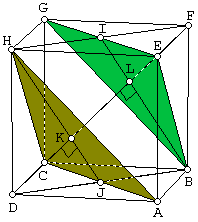
$\clubsuit \, $ Pada gambar, segitiga ACH dan EBG membagi DF (Diagonal ruang) menjadi 3 bagian sama panjang yaitu pada titik K dan L, sehingga jarak D ke segitiga EBG adalah $ \frac{2}{3} \, $ diagonal ruang.
Sehingga :
Jarak = $ \frac{2}{3} DF = \frac{2}{3} . s\sqrt{3} = \frac{2}{3}.1.\sqrt{3} = \frac{2}{3}\sqrt{3} $
Jadi, jarak D ke bidang EBG adalah $ \frac{2}{3}\sqrt{3} . \heartsuit $
$\clubsuit \, $ Gambar

$\clubsuit \, $ Pada gambar, segitiga ACH dan EBG membagi DF (Diagonal ruang) menjadi 3 bagian sama panjang yaitu pada titik K dan L, sehingga jarak D ke segitiga EBG adalah $ \frac{2}{3} \, $ diagonal ruang.
Sehingga :
Jarak = $ \frac{2}{3} DF = \frac{2}{3} . s\sqrt{3} = \frac{2}{3}.1.\sqrt{3} = \frac{2}{3}\sqrt{3} $
Jadi, jarak D ke bidang EBG adalah $ \frac{2}{3}\sqrt{3} . \heartsuit $
Nomor 2
Misalkan $ f^\prime (x) $ menyatakan turunan pertama dari fungsi $ f(x) = \frac{x^2}{3-x}, \, x \neq 3 , $ jika $ f^\prime (2) $ dan
$ \frac{f^\prime (4)}{2} $ adalah suku pertama dan kedua suatu deret geometri tak berhingga, maka jumlah deret tersebut adalah ....
$\spadesuit \, $ Konsep turunan : $y=\frac{U}{V} \rightarrow y^\prime = \frac{U^\prime .V - U. V^\prime}{V^2} $
$\spadesuit \, $ Menentukan turunan fungsinya
$\begin{align} f(x) & = \frac{x^2}{3-x} \\ U & = x^2 \rightarrow U^\prime = 2x \\ V & = 3-x \rightarrow V^\prime = -1 \\ f^\prime (x) & = \frac{U^\prime .V - U. V^\prime}{V^2} \\ f^\prime (x) & = \frac{2x. (3-x) - x^2. (-1)}{(3-x)^2} \\ f^\prime (x) & = \frac{6x-x^2}{(3-x)^2} \\ x=2 \rightarrow f^\prime (2) & = \frac{6.2-2^2}{(3-2)^2} = 8 \\ x=4 \rightarrow f^\prime (4) & = \frac{6.4-4^2}{(3-4)^2} = 8 \\ \frac{f^\prime (4)}{2} & = \frac{8}{2} = 4 \end{align}$
Sehingga barisannya :
$ f^\prime (2) , \, \frac{f^\prime (4)}{2}, ... \, \, $ yaitu 8, 4, .....
$ a = 8, \, r = \frac{U_2}{U_1} = \frac{4}{8} = \frac{1}{2} $
$\spadesuit \, $ Menentukan jumlah deret tak hingganya
$\begin{align} S_\infty = \frac{a}{1-r} = \frac{8}{1-\frac{1}{2}} = \frac{8}{\frac{1}{2}} = 16 \end{align}$
Jadi, jumlah tak hingganya adalah 16. $ \heartsuit $
$\spadesuit \, $ Menentukan turunan fungsinya
$\begin{align} f(x) & = \frac{x^2}{3-x} \\ U & = x^2 \rightarrow U^\prime = 2x \\ V & = 3-x \rightarrow V^\prime = -1 \\ f^\prime (x) & = \frac{U^\prime .V - U. V^\prime}{V^2} \\ f^\prime (x) & = \frac{2x. (3-x) - x^2. (-1)}{(3-x)^2} \\ f^\prime (x) & = \frac{6x-x^2}{(3-x)^2} \\ x=2 \rightarrow f^\prime (2) & = \frac{6.2-2^2}{(3-2)^2} = 8 \\ x=4 \rightarrow f^\prime (4) & = \frac{6.4-4^2}{(3-4)^2} = 8 \\ \frac{f^\prime (4)}{2} & = \frac{8}{2} = 4 \end{align}$
Sehingga barisannya :
$ f^\prime (2) , \, \frac{f^\prime (4)}{2}, ... \, \, $ yaitu 8, 4, .....
$ a = 8, \, r = \frac{U_2}{U_1} = \frac{4}{8} = \frac{1}{2} $
$\spadesuit \, $ Menentukan jumlah deret tak hingganya
$\begin{align} S_\infty = \frac{a}{1-r} = \frac{8}{1-\frac{1}{2}} = \frac{8}{\frac{1}{2}} = 16 \end{align}$
Jadi, jumlah tak hingganya adalah 16. $ \heartsuit $
Nomor 3
$\displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi ) \cos ^2 x}{\pi (\pi - 2x) \tan (x-\frac{\pi}{2})} = ....$
$\clubsuit \, $ Konsep dasar
$ \cos x = \sin (\frac{\pi}{2} - x ) \, \, $ atau $ \, \, \cos x = - \sin (x-\frac{\pi}{2}) $
$ \displaystyle \lim_{x \to k} \frac{\sin a f(x)}{b f(x)} = \displaystyle \lim_{x \to k} \frac{\sin a f(x)}{\tan b f(x)} = \frac{a}{b} \, $ dengan syarat $ f(k) = 0 $
$\clubsuit \, $ Memodifikasi soal
$\begin{align} & \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi ) \cos ^2 x}{\pi (\pi - 2x) \tan (x-\frac{\pi}{2})} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi ) ( - \sin (x-\frac{\pi}{2}) ) ^2 }{\pi . -2(x-\frac{\pi}{2}) \tan (x-\frac{\pi}{2})} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi )}{\pi}. \frac{\sin (x-\frac{\pi}{2})}{-2(x-\frac{\pi}{2})} . \frac{\sin (x-\frac{\pi}{2})}{\tan (x-\frac{\pi}{2})} \\ & = \frac{4(\frac{\pi}{2}-\pi )}{\pi}. \frac{1}{-2} . \frac{1}{1} \\ & = \frac{4(\frac{-\pi}{2} )}{-2\pi} = 1 \end{align}$
Jadi, nilai limitnya adalah 1. $ \heartsuit$
$ \cos x = \sin (\frac{\pi}{2} - x ) \, \, $ atau $ \, \, \cos x = - \sin (x-\frac{\pi}{2}) $
$ \displaystyle \lim_{x \to k} \frac{\sin a f(x)}{b f(x)} = \displaystyle \lim_{x \to k} \frac{\sin a f(x)}{\tan b f(x)} = \frac{a}{b} \, $ dengan syarat $ f(k) = 0 $
$\clubsuit \, $ Memodifikasi soal
$\begin{align} & \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi ) \cos ^2 x}{\pi (\pi - 2x) \tan (x-\frac{\pi}{2})} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi ) ( - \sin (x-\frac{\pi}{2}) ) ^2 }{\pi . -2(x-\frac{\pi}{2}) \tan (x-\frac{\pi}{2})} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2}} \frac{4(x-\pi )}{\pi}. \frac{\sin (x-\frac{\pi}{2})}{-2(x-\frac{\pi}{2})} . \frac{\sin (x-\frac{\pi}{2})}{\tan (x-\frac{\pi}{2})} \\ & = \frac{4(\frac{\pi}{2}-\pi )}{\pi}. \frac{1}{-2} . \frac{1}{1} \\ & = \frac{4(\frac{-\pi}{2} )}{-2\pi} = 1 \end{align}$
Jadi, nilai limitnya adalah 1. $ \heartsuit$
Nomor 4
Diketahui matriks-matriks $ A = \left( \begin{matrix} 1 & 1 & 2 \\ 2 & -1 & 1 \end{matrix} \right) \, $ dan
$ \, B^T = \left( \begin{matrix} 1 & 2 & -1 \\ -1 & 1 & 2 \end{matrix} \right) \, $ , $ B^T \, $ menyatakan transpos matriks $ B $ .
Jika det(2$AB$) = $k$. det ($(AB)^{-1}$), maka $ k = .... $
$\spadesuit \, $ Konsep dasar
Determinan : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow det(A) = ad-bc $
Invers : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{det(A)} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) $
$\spadesuit \, $ Menentukan A.B dan $ (AB)^{-1} \, $ serta determinannya
$ B^T = \left( \begin{matrix} 1 & 2 & -1 \\ -1 & 1 & 2 \end{matrix} \right) \rightarrow B = \left( \begin{matrix} 1 & -1 \\ 2 & 1 \\ -1 & 2 \end{matrix} \right) $
$ AB = \left( \begin{matrix} 1 & 1 & 2 \\ 2 & -1 & 1 \end{matrix} \right). \left( \begin{matrix} 1 & -1 \\ 2 & 1 \\ -1 & 2 \end{matrix} \right) = \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) $
$\begin{align} (AB)^{-1} & = \frac{1}{1.(-1) - (-1).4} \left( \begin{matrix} -1 & -4 \\ 1 & 1 \end{matrix} \right) \\ & = \frac{1}{3} \left( \begin{matrix} -1 & -4 \\ 1 & 1 \end{matrix} \right) = \left( \begin{matrix} \frac{-1}{3} & \frac{-4}{3} \\ \frac{1}{3} & \frac{1}{3} \end{matrix} \right) \end{align}$
$ 2AB = 2. \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) = \left( \begin{matrix} 2 & 8 \\ -2 & -2 \end{matrix} \right) $
$ det(2AB) = [2.(-2)]- [(-2).8] = -4 + 16 = 12 $
$ det ((AB)^{-1}) = [\frac{-1}{3}. \frac{1}{3}] - [\frac{1}{3} . \frac{-4}{3} ] = \frac{-1}{9} + \frac{4}{9} = \frac{3}{9} = \frac{1}{3} $
$\spadesuit \, $ Menentukan nilai $ k $
$\begin{align} det (2AB) & = k. det ((AB)^{-1}) \\ 12 & = k . \frac{1}{3} \\ k & = 36 \end{align}$
Jadi, nilai $ k \, $ adalah 36. $\heartsuit $
Determinan : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow det(A) = ad-bc $
Invers : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{det(A)} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) $
$\spadesuit \, $ Menentukan A.B dan $ (AB)^{-1} \, $ serta determinannya
$ B^T = \left( \begin{matrix} 1 & 2 & -1 \\ -1 & 1 & 2 \end{matrix} \right) \rightarrow B = \left( \begin{matrix} 1 & -1 \\ 2 & 1 \\ -1 & 2 \end{matrix} \right) $
$ AB = \left( \begin{matrix} 1 & 1 & 2 \\ 2 & -1 & 1 \end{matrix} \right). \left( \begin{matrix} 1 & -1 \\ 2 & 1 \\ -1 & 2 \end{matrix} \right) = \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) $
$\begin{align} (AB)^{-1} & = \frac{1}{1.(-1) - (-1).4} \left( \begin{matrix} -1 & -4 \\ 1 & 1 \end{matrix} \right) \\ & = \frac{1}{3} \left( \begin{matrix} -1 & -4 \\ 1 & 1 \end{matrix} \right) = \left( \begin{matrix} \frac{-1}{3} & \frac{-4}{3} \\ \frac{1}{3} & \frac{1}{3} \end{matrix} \right) \end{align}$
$ 2AB = 2. \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) = \left( \begin{matrix} 2 & 8 \\ -2 & -2 \end{matrix} \right) $
$ det(2AB) = [2.(-2)]- [(-2).8] = -4 + 16 = 12 $
$ det ((AB)^{-1}) = [\frac{-1}{3}. \frac{1}{3}] - [\frac{1}{3} . \frac{-4}{3} ] = \frac{-1}{9} + \frac{4}{9} = \frac{3}{9} = \frac{1}{3} $
$\spadesuit \, $ Menentukan nilai $ k $
$\begin{align} det (2AB) & = k. det ((AB)^{-1}) \\ 12 & = k . \frac{1}{3} \\ k & = 36 \end{align}$
Jadi, nilai $ k \, $ adalah 36. $\heartsuit $
Cara II
$\spadesuit \, $ Sifat determinan : |P| artinya determinan P atau det(P)
$|P^{-1}| = \frac{1}{|P|} \, $ dan $ \, |k.P_{m\times m}| = k^m.|P| $
$\spadesuit \, $ Menentukan determinan AB
$ AB = \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) \rightarrow |AB| = [1.(-1)] - [4.(-1)] = 3 $
$\spadesuit \, $ Menentukan nilai $ k $ dengan sifat determinan
$\begin{align} |2(AB)_{2\times 2}| & = k. |(AB)^{-1}| \\ 2^2 |AB| & = k. \frac{1}{|AB|} \\ 4. 3 & = k. \frac{1}{3} \\ 12 & = k. \frac{1}{3} \\ k & = 36 \end{align}$
Jadi, nilai $ k \, $ adalah 36. $\heartsuit $
$\spadesuit \, $ Sifat determinan : |P| artinya determinan P atau det(P)
$|P^{-1}| = \frac{1}{|P|} \, $ dan $ \, |k.P_{m\times m}| = k^m.|P| $
$\spadesuit \, $ Menentukan determinan AB
$ AB = \left( \begin{matrix} 1 & 4 \\ -1 & -1 \end{matrix} \right) \rightarrow |AB| = [1.(-1)] - [4.(-1)] = 3 $
$\spadesuit \, $ Menentukan nilai $ k $ dengan sifat determinan
$\begin{align} |2(AB)_{2\times 2}| & = k. |(AB)^{-1}| \\ 2^2 |AB| & = k. \frac{1}{|AB|} \\ 4. 3 & = k. \frac{1}{3} \\ 12 & = k. \frac{1}{3} \\ k & = 36 \end{align}$
Jadi, nilai $ k \, $ adalah 36. $\heartsuit $
Nomor 5
Jika $ 0 \leq x \leq 8 \, $ , maka nilai-nilai $ x \, $ yang memenuhi pertaksamaan $ \sin \frac{\pi x}{4} \sin \frac{\pi x}{2} > 0 \, $
adalah ....
$\clubsuit \, $ Konsep dasar persamaan trigonometri
$\sin f(x) = \sin \theta \, $ Solusinya : $ f(x) = \theta + k.2\pi \, $ dan $ \, f(x) = (\pi-\theta) + k.2\pi $
dengan $ k \, $ bilangan bulat
$\clubsuit \, $ Menentukan nilai $ x $
$\begin{align} \sin \frac{\pi x}{4} \sin \frac{\pi x}{2} & > 0 \\ \sin \frac{\pi x}{4} = 0 & \vee \sin \frac{\pi x}{2} = 0 \end{align}$
Untuk $ \sin \frac{\pi x}{4} = 0 \rightarrow \sin \frac{\pi x}{4} = \sin 0^\circ \, $ Solunsinya :
1). $ \frac{\pi x}{4} = 0^\circ + k.2\pi \rightarrow \pi x = k.8\pi \rightarrow x = 8k $
diperoleh : $ x =\{ 0, 8, 16, .... \} $
2). $ \frac{\pi x}{4} = (\pi - 0^\circ ) + k.2\pi \rightarrow \pi x = 4\pi + k.8\pi \rightarrow x = 4 + 8k $
diperoleh : $ x =\{ 4, 12, .... \} $
Untuk $ \sin \frac{\pi x}{2} = 0 \rightarrow \sin \frac{\pi x}{2} = \sin 0^\circ \, $ Solunsinya :
1). $ \frac{\pi x}{2} = 0^\circ + k.2\pi \rightarrow \pi x = k.4\pi \rightarrow x = 4k $
diperoleh : $ x =\{ 0, 4, 8, 12, .... \} $
2). $ \frac{\pi x}{2} = (\pi - 0^\circ ) + k.2\pi \rightarrow \pi x = 2\pi + k.4\pi \rightarrow x = 2 + 4k $
diperoleh : $ x =\{ 2, 6, 10, 14, .... \} $
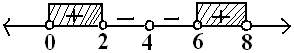
Jadi, solusinya adalah $ HP = \{0 < x < 2 \vee 6 < x < 8 \} . \heartsuit$
$\sin f(x) = \sin \theta \, $ Solusinya : $ f(x) = \theta + k.2\pi \, $ dan $ \, f(x) = (\pi-\theta) + k.2\pi $
dengan $ k \, $ bilangan bulat
$\clubsuit \, $ Menentukan nilai $ x $
$\begin{align} \sin \frac{\pi x}{4} \sin \frac{\pi x}{2} & > 0 \\ \sin \frac{\pi x}{4} = 0 & \vee \sin \frac{\pi x}{2} = 0 \end{align}$
Untuk $ \sin \frac{\pi x}{4} = 0 \rightarrow \sin \frac{\pi x}{4} = \sin 0^\circ \, $ Solunsinya :
1). $ \frac{\pi x}{4} = 0^\circ + k.2\pi \rightarrow \pi x = k.8\pi \rightarrow x = 8k $
diperoleh : $ x =\{ 0, 8, 16, .... \} $
2). $ \frac{\pi x}{4} = (\pi - 0^\circ ) + k.2\pi \rightarrow \pi x = 4\pi + k.8\pi \rightarrow x = 4 + 8k $
diperoleh : $ x =\{ 4, 12, .... \} $
Untuk $ \sin \frac{\pi x}{2} = 0 \rightarrow \sin \frac{\pi x}{2} = \sin 0^\circ \, $ Solunsinya :
1). $ \frac{\pi x}{2} = 0^\circ + k.2\pi \rightarrow \pi x = k.4\pi \rightarrow x = 4k $
diperoleh : $ x =\{ 0, 4, 8, 12, .... \} $
2). $ \frac{\pi x}{2} = (\pi - 0^\circ ) + k.2\pi \rightarrow \pi x = 2\pi + k.4\pi \rightarrow x = 2 + 4k $
diperoleh : $ x =\{ 2, 6, 10, 14, .... \} $
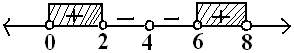
Jadi, solusinya adalah $ HP = \{0 < x < 2 \vee 6 < x < 8 \} . \heartsuit$
Jika ada masukan, saran, kritikan, alternatif penyelesaian lain yang lebih mudah, atau apapun yang berhubungan dengan halaman ini, silahkan kirim ke email : d.4rm.408@gmail.com , atau langsung isi komentar pada kotak komentar di bawah ini. Semoga bermanfaat, terima kasih.