Nomor 11
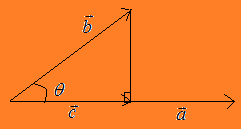
Jika $\sin \alpha + \sin \beta = 2\sqrt{A}$ dan $\cos \alpha + \cos \beta = 2\sqrt{B}$ , maka $\cos (\alpha - \beta) = ...$
$\clubsuit \, $ Rumus Dasar :
$\cos (A - B) = \cos A \cos B + \sin A \sin B \, \, \,$ dan $\, \cos ^2 x + \sin ^2 x = 1$
$\clubsuit \, $ Kuadratkan kedua persamaan dan jumlahkan :
$\begin{array}{cc} \left( \sin \alpha + \sin \beta \right) ^2 = \left( 2\sqrt{A} \right)^2 \Rightarrow \sin ^2 \alpha + \sin ^2 \beta +2 \sin \alpha \sin \beta = 4A & \\ \left( \cos \alpha + \cos \beta \right) ^2 = \left( 2\sqrt{B} \right)^2 \Rightarrow \cos ^2 \alpha + \cos ^2 \beta +2 \cos \alpha \cos \beta = 4B & + \\ \hline (\cos ^2 \alpha + \sin ^2 \alpha) + (\cos ^2 \beta + \sin ^2 \beta) +2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) = 4A + 4B & \\ 1 + 1 +2\cos (\alpha - \beta) = 4A + 4B \\ 2\cos (\alpha - \beta) = 4A + 4B - 2 \\ \cos (\alpha - \beta) = 2A + 2B - 1 \end{array}$
Jadi, nilai $\cos (\alpha - \beta) = 2A + 2B - 1. \heartsuit $
$\cos (A - B) = \cos A \cos B + \sin A \sin B \, \, \,$ dan $\, \cos ^2 x + \sin ^2 x = 1$
$\clubsuit \, $ Kuadratkan kedua persamaan dan jumlahkan :
$\begin{array}{cc} \left( \sin \alpha + \sin \beta \right) ^2 = \left( 2\sqrt{A} \right)^2 \Rightarrow \sin ^2 \alpha + \sin ^2 \beta +2 \sin \alpha \sin \beta = 4A & \\ \left( \cos \alpha + \cos \beta \right) ^2 = \left( 2\sqrt{B} \right)^2 \Rightarrow \cos ^2 \alpha + \cos ^2 \beta +2 \cos \alpha \cos \beta = 4B & + \\ \hline (\cos ^2 \alpha + \sin ^2 \alpha) + (\cos ^2 \beta + \sin ^2 \beta) +2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) = 4A + 4B & \\ 1 + 1 +2\cos (\alpha - \beta) = 4A + 4B \\ 2\cos (\alpha - \beta) = 4A + 4B - 2 \\ \cos (\alpha - \beta) = 2A + 2B - 1 \end{array}$
Jadi, nilai $\cos (\alpha - \beta) = 2A + 2B - 1. \heartsuit $
Nomor 12
Diketahui A(-3,0,0), B(0,3,0), dan C(0,0,7). Panjang vektor proyeksi $\vec{AC}$ ke vektor $\vec{AB}$ adalah ...
$\spadesuit \, $ Menentukan vektor $\vec{AC}$ dan $\vec{AB}$ :
$\vec{AC} = C - A = (3 \, \, 0 \, \, 7) $
$\vec{AB} = B-A = (3 \, \, 3 \, \, 0) $
$\vec{AC}. \vec{AB} = 3.3 + 0.3 + 7.0 = 9 + 0 + 0 =9$
panjang $\vec{AB} = | \vec{AB} | = \sqrt{3^2+3^2+0^2} = \sqrt{18} = 3\sqrt{2}$
$\spadesuit \, $ Menentukan Panjang vektor proyeksi $\vec{AC}$ ke vektor $\vec{AB}$
Panjang Proyeksi = $\frac{\vec{AC}. \vec{AB}}{| \vec{AB} |} = \frac{9}{3\sqrt{2}} = \frac{3\sqrt{2}}{2}$
Jadi, Panjang Proyeksi adalah $ \frac{3\sqrt{2}}{2} . \heartsuit $
$\vec{AC} = C - A = (3 \, \, 0 \, \, 7) $
$\vec{AB} = B-A = (3 \, \, 3 \, \, 0) $
$\vec{AC}. \vec{AB} = 3.3 + 0.3 + 7.0 = 9 + 0 + 0 =9$
panjang $\vec{AB} = | \vec{AB} | = \sqrt{3^2+3^2+0^2} = \sqrt{18} = 3\sqrt{2}$
$\spadesuit \, $ Menentukan Panjang vektor proyeksi $\vec{AC}$ ke vektor $\vec{AB}$
Panjang Proyeksi = $\frac{\vec{AC}. \vec{AB}}{| \vec{AB} |} = \frac{9}{3\sqrt{2}} = \frac{3\sqrt{2}}{2}$
Jadi, Panjang Proyeksi adalah $ \frac{3\sqrt{2}}{2} . \heartsuit $
Nomor 13
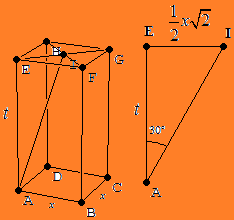
Diketahui kubus ABCD.EFGH mempunyai sisi 4 cm. Titik P pada BC sehingga PB = 1 cm, titik Q pada GH sehingga HQ = 1 cm,
R titik tengah AE. Jarak R ke PQ adalah ...
$\spadesuit \, $ Gambarnya :


Jarak R ke garis PQ sama dengan panjang garis RN.
$\spadesuit \, $ Menentukan panjang sisi pada segitiga PQR
$\Delta ABP, \, AP = \sqrt{4^2+1^2} = \sqrt{17} $
$\Delta APR, \, PR = \sqrt{2^2+(\sqrt{17})^2} = \sqrt{21} $
dari gambar, panjang PR = RQ = $\sqrt{21} $
$\Delta CGQ, \, CQ = \sqrt{4^2+3^2} = 5 $
$\Delta CPQ, \, PQ = \sqrt{5^2+3^2} = \sqrt{34} $
$\spadesuit \, $ Segitiga PQR sama kaki sehingga panjang QN = NP = $\frac{1}{2}PQ = \frac{1}{2}\sqrt{34}$
$\spadesuit \, $ Menentukan panjang garis RN
$\Delta PNR, \, RN = \sqrt{PR^2-PN^2} = \sqrt{(\sqrt{21})^2-\left( \frac{1}{2}\sqrt{34}\right)^2} = \frac{5}{2}\sqrt{2} . $
Jadi, Jaraknya adalah $ \frac{5}{2}\sqrt{2} . \heartsuit $


Jarak R ke garis PQ sama dengan panjang garis RN.
$\spadesuit \, $ Menentukan panjang sisi pada segitiga PQR
$\Delta ABP, \, AP = \sqrt{4^2+1^2} = \sqrt{17} $
$\Delta APR, \, PR = \sqrt{2^2+(\sqrt{17})^2} = \sqrt{21} $
dari gambar, panjang PR = RQ = $\sqrt{21} $
$\Delta CGQ, \, CQ = \sqrt{4^2+3^2} = 5 $
$\Delta CPQ, \, PQ = \sqrt{5^2+3^2} = \sqrt{34} $
$\spadesuit \, $ Segitiga PQR sama kaki sehingga panjang QN = NP = $\frac{1}{2}PQ = \frac{1}{2}\sqrt{34}$
$\spadesuit \, $ Menentukan panjang garis RN
$\Delta PNR, \, RN = \sqrt{PR^2-PN^2} = \sqrt{(\sqrt{21})^2-\left( \frac{1}{2}\sqrt{34}\right)^2} = \frac{5}{2}\sqrt{2} . $
Jadi, Jaraknya adalah $ \frac{5}{2}\sqrt{2} . \heartsuit $
Nomor 14
Diketahui $f(x)=\frac{2}{3}x^3-\frac{1}{2}x^2-3x+\frac{1}{6}$ . Jika $g(x)=f(1-x)$ , maka $g$ naik pada selang ...
$\spadesuit \, $ Menentukan fungsi $g(x)$ dan turunannya :
$\begin{align*} g(x) & = f(1-x) \\ g(x) & = \frac{2}{3}(1-x)^3-\frac{1}{2}(1-x)^2-3(1-x)+\frac{1}{6} \\ g^\prime (x) & = \frac{2}{3} . 3.(1-x)^2 . (-1) - \frac{1}{2}. 2. (1-x) . (-1) + 3 \\ & = -2(x^2-2x+1) + (1-x) + 3 \\ g^\prime (x) &= -2x^2 + 3x + 2 \end{align*}$
$\spadesuit \, $ Syarat fungsi $g(x)$ naik : $ g^\prime (x) > 0$
$\begin{align*} g^\prime (x) & > 0 \\ -2x^2 + 3x + 2 & > 0 \, \, \text{(kali -1 dan tanda dibalik)} \\ 2x^2-3x-2 & < 0 \\ (2x+1)(x-2) & < 0 \\ x = -\frac{1}{2} & \vee x = 2 \end{align*}$
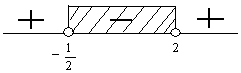
Jadi, interval naiknya adalah $ -\frac{1}{2} < x < 2 . \heartsuit $
$\begin{align*} g(x) & = f(1-x) \\ g(x) & = \frac{2}{3}(1-x)^3-\frac{1}{2}(1-x)^2-3(1-x)+\frac{1}{6} \\ g^\prime (x) & = \frac{2}{3} . 3.(1-x)^2 . (-1) - \frac{1}{2}. 2. (1-x) . (-1) + 3 \\ & = -2(x^2-2x+1) + (1-x) + 3 \\ g^\prime (x) &= -2x^2 + 3x + 2 \end{align*}$
$\spadesuit \, $ Syarat fungsi $g(x)$ naik : $ g^\prime (x) > 0$
$\begin{align*} g^\prime (x) & > 0 \\ -2x^2 + 3x + 2 & > 0 \, \, \text{(kali -1 dan tanda dibalik)} \\ 2x^2-3x-2 & < 0 \\ (2x+1)(x-2) & < 0 \\ x = -\frac{1}{2} & \vee x = 2 \end{align*}$

Jadi, interval naiknya adalah $ -\frac{1}{2} < x < 2 . \heartsuit $
Nomor 10
Diketahui $F(x)=(1+a)x^3-3bx^2-3x$ . Jika $F^{\prime \prime} $ habis dibagi $x+1$ , maka kurva $y=F(x)$ tidak mempunyai titik
ekstrem lokal jika ...
$\clubsuit \, $ Menentukan turunan kedua dari $F(x)$ :
$\begin{align*} F(x) & = (1+a)x^3-3bx^2-3x \\ F^\prime (x) & = 3(1+a)x^2 - 6bx - 3 \\ F^{\prime \prime } (x) & = 6(1+a)x - 6b \end{align*}$
$\clubsuit \, F^{\prime \prime} (x) $ habis dibagi $x+1$, artinya $F^{\prime \prime} (-1) = 0$
$F^{\prime \prime} (-1) = 0 \Rightarrow 6(1+a).(-1) - 6b = 0 \Rightarrow a = -b - 1$
$\clubsuit \, $ Substitusi $ a = -b - 1 \, \, $ ke turunan pertama :
$\begin{align*} F^\prime (x) & = 3(1+a)x^2 - 6bx - 3 \\ & = 3(1+-b - 1)x^2 - 6bx - 3 \\ F^\prime (x) & = -3bx^2 - 6bx - 3 \end{align*}$
$\clubsuit \, $ Menentukan titik ekstrim : Syarat $ F^\prime (x) = 0$
diperoleh : $ F^\prime (x) = 0 \Rightarrow -3bx^2 - 6bx - 3 = 0 \, $
(kali -1 dan bagi 3) $\, bx^2 + 2bx + 1 = 0 \, $ ...pers(i)
$\clubsuit \, $ Agar $F(x) \, $ tidak punya invers, maka pers(i) harus tidak mempunyai penyelesaian (tidak punya akar). Karena pers(i) bentuknya persamaan kuadrat, agar tidak punya akar nilai Diskriminannya harus kurang dari nol ($D < 0 $).
$\begin{align*} D & < 0 \\ b^2 - 4ac & < 0 \\ (2b)^2 - 4.b.1 & < 0 \\ 4b^2 - 4b & < 0 \\ 4b(b-1) & < 0 \\ b=0 \, & \vee \, b = 1 \end{align*}$
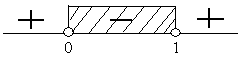
Jadi, agar $y=F(x) \, $ tidak punya titik ekstrim syaratnya adalah $0 < b < 1 . \heartsuit $
$\begin{align*} F(x) & = (1+a)x^3-3bx^2-3x \\ F^\prime (x) & = 3(1+a)x^2 - 6bx - 3 \\ F^{\prime \prime } (x) & = 6(1+a)x - 6b \end{align*}$
$\clubsuit \, F^{\prime \prime} (x) $ habis dibagi $x+1$, artinya $F^{\prime \prime} (-1) = 0$
$F^{\prime \prime} (-1) = 0 \Rightarrow 6(1+a).(-1) - 6b = 0 \Rightarrow a = -b - 1$
$\clubsuit \, $ Substitusi $ a = -b - 1 \, \, $ ke turunan pertama :
$\begin{align*} F^\prime (x) & = 3(1+a)x^2 - 6bx - 3 \\ & = 3(1+-b - 1)x^2 - 6bx - 3 \\ F^\prime (x) & = -3bx^2 - 6bx - 3 \end{align*}$
$\clubsuit \, $ Menentukan titik ekstrim : Syarat $ F^\prime (x) = 0$
diperoleh : $ F^\prime (x) = 0 \Rightarrow -3bx^2 - 6bx - 3 = 0 \, $
(kali -1 dan bagi 3) $\, bx^2 + 2bx + 1 = 0 \, $ ...pers(i)
$\clubsuit \, $ Agar $F(x) \, $ tidak punya invers, maka pers(i) harus tidak mempunyai penyelesaian (tidak punya akar). Karena pers(i) bentuknya persamaan kuadrat, agar tidak punya akar nilai Diskriminannya harus kurang dari nol ($D < 0 $).
$\begin{align*} D & < 0 \\ b^2 - 4ac & < 0 \\ (2b)^2 - 4.b.1 & < 0 \\ 4b^2 - 4b & < 0 \\ 4b(b-1) & < 0 \\ b=0 \, & \vee \, b = 1 \end{align*}$

Jadi, agar $y=F(x) \, $ tidak punya titik ekstrim syaratnya adalah $0 < b < 1 . \heartsuit $