Nomor 11
Diketahui $1+{}^{3}\log (\tan x)+({}^{3}\log (\tan x))^2 + ({}^{3}\log (\tan x))^3+...= \frac{2}{3}$, dengan $0\leq x \leq \pi , x\neq \frac{\pi}{2}$,
nilai $\sin 2x$ adalah ...
$\clubsuit \, $ Deret geometri tak hingga : $s_\infty=\frac{a}{1-r}$
$1+{}^{3}log(tanx)+({}^{3}log(tanx))^2 + ({}^{3}log(tanx))^3+... \, $ memiliki $a=1\,$ dan $r=\frac{u_2}{u_1}=\frac{{}^{3}log(tanx)}{1}={}^{3}log(tanx)$
$\clubsuit \, $ Menyederhanakan persamaan :
$\begin{align*} 1+{}^{3}log(tanx)+({}^{3}log(tanx))^2 &+ ({}^{3}log(tanx))^3+...= \frac{2}{3} \\ s_\infty=\frac{a}{1-r}&= \frac{2}{3} \\ \frac{1}{1-{}^{3}log(tanx)}&=\frac{2}{3} \\ 2.(1-{}^{3}log(tanx))&=3 \\ 2.{}^{3}log(tanx)&=-1 \\ {}^{3}log(tanx)&=-\frac{1}{2} \\ tanx&=3^{-\frac{1}{2}}=\frac{1}{\sqrt{3}} \Leftrightarrow \sqrt{3} = \frac{1}{tanx} \end{align*}$
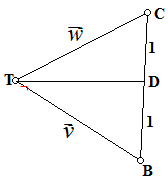
$\clubsuit \, $ Buat segitiga:

$\clubsuit \, $ Menentukan $sin2x$ :
$\begin{align*} sin2x&=2sinx.cosx \\ &=2. \frac{1}{2}.\frac{\sqrt{3}}{2} \\ sin2x&=\frac{\sqrt{3}}{2} = \frac{\frac{1}{tanx}}{2} \\ sin2x&=\frac{1}{2tanx} \end{align*}$
Jadi, nilai $sin2x=\frac{1}{2tanx}. \heartsuit $
$1+{}^{3}log(tanx)+({}^{3}log(tanx))^2 + ({}^{3}log(tanx))^3+... \, $ memiliki $a=1\,$ dan $r=\frac{u_2}{u_1}=\frac{{}^{3}log(tanx)}{1}={}^{3}log(tanx)$
$\clubsuit \, $ Menyederhanakan persamaan :
$\begin{align*} 1+{}^{3}log(tanx)+({}^{3}log(tanx))^2 &+ ({}^{3}log(tanx))^3+...= \frac{2}{3} \\ s_\infty=\frac{a}{1-r}&= \frac{2}{3} \\ \frac{1}{1-{}^{3}log(tanx)}&=\frac{2}{3} \\ 2.(1-{}^{3}log(tanx))&=3 \\ 2.{}^{3}log(tanx)&=-1 \\ {}^{3}log(tanx)&=-\frac{1}{2} \\ tanx&=3^{-\frac{1}{2}}=\frac{1}{\sqrt{3}} \Leftrightarrow \sqrt{3} = \frac{1}{tanx} \end{align*}$
$\clubsuit \, $ Buat segitiga:

$\clubsuit \, $ Menentukan $sin2x$ :
$\begin{align*} sin2x&=2sinx.cosx \\ &=2. \frac{1}{2}.\frac{\sqrt{3}}{2} \\ sin2x&=\frac{\sqrt{3}}{2} = \frac{\frac{1}{tanx}}{2} \\ sin2x&=\frac{1}{2tanx} \end{align*}$
Jadi, nilai $sin2x=\frac{1}{2tanx}. \heartsuit $
Nomor 12
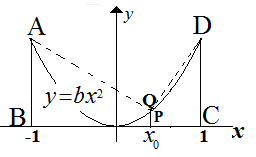
Misalkan $A(t)$ menyatakan luas daerah di bawah kurva $y=bx^2 , 0\leq x \leq t$. Jika titik $P(x_0,0)$ sehingga $A(x_0):A(1)=1:8$, maka perbandingan
luas trapesium $ABPQ:DCPQ=...$

$\spadesuit \, $ Menentukan $A(t)$:
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
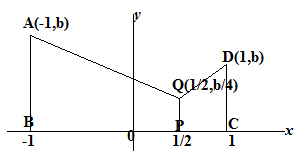
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
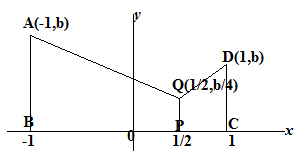
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
Nomor 13
Penyelesaian pertidaksamaan ${}^{\frac{1}{(|x|+1)}} \log (2x+3) < 1 $ adalah ...
$\spadesuit \, $ Definisi harga mutlak : $|x| = \left\{ \begin{array}{cc} x \, , & \text{untuk} \, x\geq 0 \\ -x \, , & \text{untuk} \, x<0 \end{array} \right.$
$\spadesuit \, {}^{f(x)}log [g(x)]=h(x) \, $ syarat logaritma : $f(x)>0, f(x)\neq 1, g(x)>0$
$\spadesuit \, $ Untuk $x \geq 0 \,$ maka $|x|=x:$
${}^{\frac{1}{(|x|+1)}} log (2x+3) < 1 \Leftrightarrow {}^{\frac{1}{(x+1)}} log (2x+3) < 1$
Syarat logaritma:
$(2x+3)>0 \Rightarrow x > -\frac{3}{2} \, \text{...HP}_1 $
$\frac{1}{(x+1)} > 0 \Rightarrow x>-1 \, \text{...HP}_2$
$\frac{1}{(x+1)} \neq 1 \Rightarrow x \neq 0 \, \text{...HP}_3$
untuk $x>0$ , maka $0<\frac{1}{(x+1)}<1 \,$ sehingga tanda pertidaksamaan dibalik :
$\begin{align*} {}^{\frac{1}{(x+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(x+1)}} log (2x+3) &< {}^{\frac{1}{(x+1)}} log\frac{1}{(x+1)} \\ (2x+3) &> \frac{1}{(x+1)} \\ \frac{(2x+3)(x+1)-1}{(x+1)} &>0 \\ \frac{2x^2+5x+2}{(x+1)} &>0 \\ \frac{(2x+1)(x+2)}{(x+1)} &>0\\ x=-2, \, x=-1 , \, &\text{atau} \, x=-\frac{1}{2} \end{align*}$

$\text{HP}_4 = \{ -2 < x < -1 \, \text{atau} \, x>-\frac{1}{2} \} $
sehingga : $\text{HP}_A = \text{HP}_1 \cap \text{HP}_2 \cap \text{HP}_3 \cap \text{HP}_4 = \{ x > 0 \}$
$\spadesuit \, $ Untuk $x < 0 \,$ maka $|x|=-x:$
${}^{\frac{1}{(|x|+1)}} log (2x+3) < 1 \Leftrightarrow {}^{\frac{1}{(-x+1)}} log (2x+3) < 1$
Syarat logaritma:
$(2x+3)>0 \Rightarrow x > -\frac{3}{2} \, \text{...HP}_1 $
$\frac{1}{(-x+1)} > 0 \Rightarrow x<1 \, \text{...HP}_2$
$\frac{1}{(x+1)} \neq 1 \Rightarrow x \neq 0 \, \text{...HP}_3$
untuk $x<0$ , maka $0<\frac{1}{(-x+1)}<1 \,$ sehingga tanda pertidaksamaan dibalik :
$\begin{align*} {}^{\frac{1}{(-x+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(-x+1)}} log (2x+3) &< {}^{\frac{1}{(-x+1)}} log\frac{1}{(-x+1)} \\ (2x+3) &> \frac{1}{(-x+1)} \\ \frac{(2x+3)(-x+1)-1}{(-x+1)} &>0 \\ \frac{-2x^2-x+2}{(-x+1)} &>0 \\ -2x^2-x+2=0 &\Rightarrow x = \frac{1\pm \sqrt{1+16}}{-4} =\frac{-1 \pm \sqrt{1+16}}{4} \\ -x+1=0 &\Rightarrow x = 1 \end{align*}$

$\text{HP}_4 = \{ \frac{-1 - \sqrt{1+16}}{4} < x < \frac{-1 + \sqrt{1+16}}{4} \, \text{atau} \, x>1 \} $
sehingga : $\text{HP}_B = \text{HP}_1 \cap \text{HP}_2 \cap \text{HP}_3 \cap \text{HP}_4 = \{ -\frac{3}{2}< x < 0 \}$
Jadi, Solusinya : $\text{HP}=\text{HP}_A \cup \text{HP}_B = \{ -\frac{3}{2}< x < 1 \, \text{atau} \, x>0 \} . \heartsuit $
$\spadesuit \, {}^{f(x)}log [g(x)]=h(x) \, $ syarat logaritma : $f(x)>0, f(x)\neq 1, g(x)>0$
$\spadesuit \, $ Untuk $x \geq 0 \,$ maka $|x|=x:$
${}^{\frac{1}{(|x|+1)}} log (2x+3) < 1 \Leftrightarrow {}^{\frac{1}{(x+1)}} log (2x+3) < 1$
Syarat logaritma:
$(2x+3)>0 \Rightarrow x > -\frac{3}{2} \, \text{...HP}_1 $
$\frac{1}{(x+1)} > 0 \Rightarrow x>-1 \, \text{...HP}_2$
$\frac{1}{(x+1)} \neq 1 \Rightarrow x \neq 0 \, \text{...HP}_3$
untuk $x>0$ , maka $0<\frac{1}{(x+1)}<1 \,$ sehingga tanda pertidaksamaan dibalik :
$\begin{align*} {}^{\frac{1}{(x+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(x+1)}} log (2x+3) &< {}^{\frac{1}{(x+1)}} log\frac{1}{(x+1)} \\ (2x+3) &> \frac{1}{(x+1)} \\ \frac{(2x+3)(x+1)-1}{(x+1)} &>0 \\ \frac{2x^2+5x+2}{(x+1)} &>0 \\ \frac{(2x+1)(x+2)}{(x+1)} &>0\\ x=-2, \, x=-1 , \, &\text{atau} \, x=-\frac{1}{2} \end{align*}$

$\text{HP}_4 = \{ -2 < x < -1 \, \text{atau} \, x>-\frac{1}{2} \} $
sehingga : $\text{HP}_A = \text{HP}_1 \cap \text{HP}_2 \cap \text{HP}_3 \cap \text{HP}_4 = \{ x > 0 \}$
$\spadesuit \, $ Untuk $x < 0 \,$ maka $|x|=-x:$
${}^{\frac{1}{(|x|+1)}} log (2x+3) < 1 \Leftrightarrow {}^{\frac{1}{(-x+1)}} log (2x+3) < 1$
Syarat logaritma:
$(2x+3)>0 \Rightarrow x > -\frac{3}{2} \, \text{...HP}_1 $
$\frac{1}{(-x+1)} > 0 \Rightarrow x<1 \, \text{...HP}_2$
$\frac{1}{(x+1)} \neq 1 \Rightarrow x \neq 0 \, \text{...HP}_3$
untuk $x<0$ , maka $0<\frac{1}{(-x+1)}<1 \,$ sehingga tanda pertidaksamaan dibalik :
$\begin{align*} {}^{\frac{1}{(-x+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(-x+1)}} log (2x+3) &< {}^{\frac{1}{(-x+1)}} log\frac{1}{(-x+1)} \\ (2x+3) &> \frac{1}{(-x+1)} \\ \frac{(2x+3)(-x+1)-1}{(-x+1)} &>0 \\ \frac{-2x^2-x+2}{(-x+1)} &>0 \\ -2x^2-x+2=0 &\Rightarrow x = \frac{1\pm \sqrt{1+16}}{-4} =\frac{-1 \pm \sqrt{1+16}}{4} \\ -x+1=0 &\Rightarrow x = 1 \end{align*}$

$\text{HP}_4 = \{ \frac{-1 - \sqrt{1+16}}{4} < x < \frac{-1 + \sqrt{1+16}}{4} \, \text{atau} \, x>1 \} $
sehingga : $\text{HP}_B = \text{HP}_1 \cap \text{HP}_2 \cap \text{HP}_3 \cap \text{HP}_4 = \{ -\frac{3}{2}< x < 0 \}$
Jadi, Solusinya : $\text{HP}=\text{HP}_A \cup \text{HP}_B = \{ -\frac{3}{2}< x < 1 \, \text{atau} \, x>0 \} . \heartsuit $
$\spadesuit \, $ Cara II : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow {}^{\frac{1}{(|x|+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(|1|+1)}} log (2.1+3) &< 1 \\ {}^{\frac{1}{2}} log (5) &< 1 \\ {}^{2^{-1}} log (5) &< 1 \\ -\left( {}^{2} log (5) \right) &< 1 \, \, \text{(benar)} \end{align*}$
yang ada $x=1$ benar, opsi yang salah adalah A dan E.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow {}^{\frac{1}{(|x|+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(|-1|+1)}} log (2.(-1)+3) &< 1 \\ {}^{\frac{1}{2}} log (1) &< 1 \\ 0 &< 1 \, \, \text{(benar)} \end{align*}$
yang ada $x=-1$ benar, opsi yang salah adalah B dan C.
Jadi, opsi yang benar adalah D yaitu $\text{HP}= \{ -\frac{3}{2}< x < 1 \, \text{atau} \, x>0 \} . \heartsuit $
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow {}^{\frac{1}{(|x|+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(|1|+1)}} log (2.1+3) &< 1 \\ {}^{\frac{1}{2}} log (5) &< 1 \\ {}^{2^{-1}} log (5) &< 1 \\ -\left( {}^{2} log (5) \right) &< 1 \, \, \text{(benar)} \end{align*}$
yang ada $x=1$ benar, opsi yang salah adalah A dan E.
$\begin{align*} \text{Pilih} \, x=-1 \Rightarrow {}^{\frac{1}{(|x|+1)}} log (2x+3) &< 1 \\ {}^{\frac{1}{(|-1|+1)}} log (2.(-1)+3) &< 1 \\ {}^{\frac{1}{2}} log (1) &< 1 \\ 0 &< 1 \, \, \text{(benar)} \end{align*}$
yang ada $x=-1$ benar, opsi yang salah adalah B dan C.
Jadi, opsi yang benar adalah D yaitu $\text{HP}= \{ -\frac{3}{2}< x < 1 \, \text{atau} \, x>0 \} . \heartsuit $
Nomor 14
Diketahui $Q(x)$ suatu polinomial. Jika $(xQ(x))^2-6xQ(x)$ dan $Q(x^2-6x)$ berturut-turut memberikan sisa -9 dan 9 apabila masing-masing dibagi $x-1$,
maka $Q(x)$ dibagi $x^2+4x-5$ memberikan sisa ...
$\spadesuit \, $ Teorema sisa : $\frac{f(x)}{x-a} \Rightarrow \text{sisa} = f(a)$
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
$\spadesuit \, \frac{\left( xQ(x) \right)^2-6xQ(x)}{x-1} \Rightarrow \text{sisa} = -9$
artinya : substitusi $x=1\, $ ke $(xQ(x))^2-6xQ(x)$ hasilnya -9
$\begin{align*} (1.Q(1))^2-6.1.Q(1)&=-9 \\ (Q(1))^2-6Q(1)+9&=0 \\ (Q(1)-3)^2&=0 \\ Q(1)&=3 \, \text{...pers(i)} \end{align*}$
$\spadesuit \, \frac{Q(x^2-6x)}{x-1} \Rightarrow \text{sisa} = 9$
artinya : substitusi $x=1\, $ ke $Q(x^2-6x)$ hasilnya 9
$\begin{align*} Q(1^2-6.1)&=9 \\ Q(-5)&=9 \, \text{...pers(ii)} \end{align*}$
$\spadesuit \, Q(x) \, $ dibagi dengan $x^2+4x-5$ dengan hasil $h(x)$ dan misalkan sisanya $ax+b$ , serta gunakan pers(i) dan pers(ii) :
$\begin{align*} Q(x)&=(x^2+4x-5).h(x)+ (ax+b) \\ Q(x)&=(x-1)(x+5).h(x)+ (ax+b) \\ x=1 \Rightarrow Q(1)&=(1-1)(1+5).h(1)+ (a.1+b) \\ &\Leftrightarrow a+b=3 \, \text{...pers(iii)} \\ x=-5 \Rightarrow Q(-5)&=(-5-1)(-5+5).h(-5)+ (a.-5+b) \\ &\Leftrightarrow -5a+b=9 \, \text{...pers(iv)} \end{align*}$
$\spadesuit \, $ Eliminasi pers(iii) dan pers(iv), diperoleh $a=-1 \, $ dan $b=4 \, $.
Jadi, sisanya adalah $ax+b=-x+4 .\, \heartsuit $
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
$\spadesuit \, \frac{\left( xQ(x) \right)^2-6xQ(x)}{x-1} \Rightarrow \text{sisa} = -9$
artinya : substitusi $x=1\, $ ke $(xQ(x))^2-6xQ(x)$ hasilnya -9
$\begin{align*} (1.Q(1))^2-6.1.Q(1)&=-9 \\ (Q(1))^2-6Q(1)+9&=0 \\ (Q(1)-3)^2&=0 \\ Q(1)&=3 \, \text{...pers(i)} \end{align*}$
$\spadesuit \, \frac{Q(x^2-6x)}{x-1} \Rightarrow \text{sisa} = 9$
artinya : substitusi $x=1\, $ ke $Q(x^2-6x)$ hasilnya 9
$\begin{align*} Q(1^2-6.1)&=9 \\ Q(-5)&=9 \, \text{...pers(ii)} \end{align*}$
$\spadesuit \, Q(x) \, $ dibagi dengan $x^2+4x-5$ dengan hasil $h(x)$ dan misalkan sisanya $ax+b$ , serta gunakan pers(i) dan pers(ii) :
$\begin{align*} Q(x)&=(x^2+4x-5).h(x)+ (ax+b) \\ Q(x)&=(x-1)(x+5).h(x)+ (ax+b) \\ x=1 \Rightarrow Q(1)&=(1-1)(1+5).h(1)+ (a.1+b) \\ &\Leftrightarrow a+b=3 \, \text{...pers(iii)} \\ x=-5 \Rightarrow Q(-5)&=(-5-1)(-5+5).h(-5)+ (a.-5+b) \\ &\Leftrightarrow -5a+b=9 \, \text{...pers(iv)} \end{align*}$
$\spadesuit \, $ Eliminasi pers(iii) dan pers(iv), diperoleh $a=-1 \, $ dan $b=4 \, $.
Jadi, sisanya adalah $ax+b=-x+4 .\, \heartsuit $
Nomor 15
Jika $A$ adalah matriks berukuran 2 x 2 dan
$\left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] = x^2+5x+8$, maka matriks $A$
yang mungkin adalah ...
$\clubsuit \, $ Misalkan matriks $A=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \, $:
$\begin{align*} \left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ \left[ \begin{matrix} x & 1 \end{matrix} \right] \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ \left[ \begin{matrix} ax+c & bx+d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ ax^2+(b+c)x+d&= x^2+5x+8 \end{align*}$
$\clubsuit \, $ Diperoleh $a=1,d=8, \, $ dan $b+c=5$
Jadi, kemungkinan matriks $A$: $\, \, A=\left[ \begin{matrix} 1 & -3 \\ 8 & 8 \end{matrix} \right]\, \heartsuit $
$\begin{align*} \left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ \left[ \begin{matrix} x & 1 \end{matrix} \right] \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ \left[ \begin{matrix} ax+c & bx+d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= x^2+5x+8 \\ ax^2+(b+c)x+d&= x^2+5x+8 \end{align*}$
$\clubsuit \, $ Diperoleh $a=1,d=8, \, $ dan $b+c=5$
Jadi, kemungkinan matriks $A$: $\, \, A=\left[ \begin{matrix} 1 & -3 \\ 8 & 8 \end{matrix} \right]\, \heartsuit $