Nomor 1
Jika $ \alpha $ dan $ \beta $ berturut-turut merupakan sudut lancip yang dibentuk oleh sumbu X dengan garis singgung $ y = x^2 - 4x - 5 $
di titik dengan absis -1 dan 3, maka $ \tan (\beta - \alpha ) = .... $
$\clubsuit \, $ Menentukan turunan
$ y = x^2 - 4x - 5 \rightarrow y^\prime = 2x - 4 $
$\clubsuit \, $ Menentukan gradien
$ x = -1 \rightarrow m_1 = f^\prime (-1) = 2.(-1)-4 = -6 $
artinya $ \tan \alpha = m_1 \rightarrow \tan \alpha = -6 $
$ x = 3 \rightarrow m_2 = f^\prime (3) = 2.3-4 = 2 $
artinya $ \tan \beta = m_2 \rightarrow \tan \beta = 2 $
$\clubsuit \, $ Menentukan nilai $ \, \tan (\beta - \alpha ) $
$\begin{align} \tan (\beta - \alpha ) & = \frac{\tan \beta - \tan \alpha}{1 + \tan \beta . \tan \alpha} \\ & = \frac{2 - (-6) }{1 + 2.(-6)} \\ & = \frac{8 }{-11} = - \frac{8 }{11} \end{align}$
Jadi, nilai $ \tan (\beta - \alpha ) = - \frac{8 }{11} . \heartsuit $
$ y = x^2 - 4x - 5 \rightarrow y^\prime = 2x - 4 $
$\clubsuit \, $ Menentukan gradien
$ x = -1 \rightarrow m_1 = f^\prime (-1) = 2.(-1)-4 = -6 $
artinya $ \tan \alpha = m_1 \rightarrow \tan \alpha = -6 $
$ x = 3 \rightarrow m_2 = f^\prime (3) = 2.3-4 = 2 $
artinya $ \tan \beta = m_2 \rightarrow \tan \beta = 2 $
$\clubsuit \, $ Menentukan nilai $ \, \tan (\beta - \alpha ) $
$\begin{align} \tan (\beta - \alpha ) & = \frac{\tan \beta - \tan \alpha}{1 + \tan \beta . \tan \alpha} \\ & = \frac{2 - (-6) }{1 + 2.(-6)} \\ & = \frac{8 }{-11} = - \frac{8 }{11} \end{align}$
Jadi, nilai $ \tan (\beta - \alpha ) = - \frac{8 }{11} . \heartsuit $
Nomor 2
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P pada CG dan titik Q pada DH dan CP = DQ = 1 cm, maka bidang PQEF mengiris kuus tersebut menjadi
dua bagian. Volume bagian yang lebih besar adalah .....
$\spadesuit \, $ Gambar
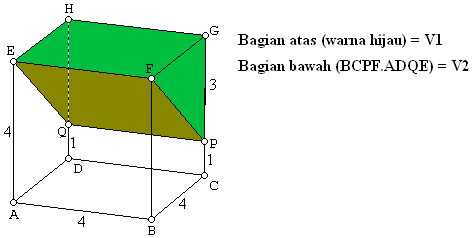
$\spadesuit \, $ Menentukan volume atas (prisma FPG.EQH)
$\begin{align} V_1 & = L_{alas} . t \\ & = (\frac{1}{2}.PG.GF).FE \\ & = (\frac{1}{2}.3.4).4 \\ V_1 & = 24 \end{align}$
$\spadesuit \, $ Menentukan volume bawah (prisma BCPF.ADQE)
$\begin{align} V_2 & = L_{alas} . t \\ & = \left[ \frac{1}{2}.(CP+FB).BC \right].AB \\ & = \left[ \frac{1}{2}.(1+4).4 \right].4 \\ V_2 & = 40 \end{align}$
Jadi, volume yang paling besar adalah 40 cm$^3 . \heartsuit $

$\spadesuit \, $ Menentukan volume atas (prisma FPG.EQH)
$\begin{align} V_1 & = L_{alas} . t \\ & = (\frac{1}{2}.PG.GF).FE \\ & = (\frac{1}{2}.3.4).4 \\ V_1 & = 24 \end{align}$
$\spadesuit \, $ Menentukan volume bawah (prisma BCPF.ADQE)
$\begin{align} V_2 & = L_{alas} . t \\ & = \left[ \frac{1}{2}.(CP+FB).BC \right].AB \\ & = \left[ \frac{1}{2}.(1+4).4 \right].4 \\ V_2 & = 40 \end{align}$
Jadi, volume yang paling besar adalah 40 cm$^3 . \heartsuit $
Nomor 3
Si A kuliah pada perguruan tinggi selama 8 semester. Besar SPP yang harus dibayar pada setiap semesternya adalah Rp.200.000 lebih besar dari SPP semester sebelumnya.
Jika pada semester ke-8 dia membayar Rp.2.400.000, maka total SPP yang dibayar selama 8 semester adalah ....
$\clubsuit \, $ Barisan aritmatika : $ U_n = a+(n-1)b \, $ dan $ \, S_n = \frac{n}{2}(2a+(n-1)b) $
$\clubsuit \, $ Menentukan nilai $ a $ (suku pertamanya) dari $ b =200.000 \, $ dan $ U_8 = 2.400.000 $
$\begin{align} U_8 & = 2400000 \\ a+7b & = 2400000 \\ a+7.(200000) & = 2400000 \\ a & = 1.000.000 \end{align}$
$\clubsuit \, $ Menentukan jumlah semua SPP ($S_8$)
$\begin{align} S_n & = \frac{n}{2}(2a+(n-1)b) \\ S_8 & = \frac{8}{2}(2a+(8-1)b) \\ S_8 & = 4.(2\times 1000000+7 \times 200000) \\ & = 4.(3400000) = 13.600.000 \end{align}$
Jadi, total SPP nya adalah Rp.13.600.000. $ \heartsuit$
$\clubsuit \, $ Menentukan nilai $ a $ (suku pertamanya) dari $ b =200.000 \, $ dan $ U_8 = 2.400.000 $
$\begin{align} U_8 & = 2400000 \\ a+7b & = 2400000 \\ a+7.(200000) & = 2400000 \\ a & = 1.000.000 \end{align}$
$\clubsuit \, $ Menentukan jumlah semua SPP ($S_8$)
$\begin{align} S_n & = \frac{n}{2}(2a+(n-1)b) \\ S_8 & = \frac{8}{2}(2a+(8-1)b) \\ S_8 & = 4.(2\times 1000000+7 \times 200000) \\ & = 4.(3400000) = 13.600.000 \end{align}$
Jadi, total SPP nya adalah Rp.13.600.000. $ \heartsuit$
Nomor 4
$\displaystyle \lim_{x \to 0} \frac{x^2\sqrt{4-x^3}}{\cos x - \cos 3x} = .... $
$\spadesuit \, $ Konsep dasar
Limit : $\displaystyle \lim_{x \to 0} \frac{ax}{\sin bx} = \frac{a}{b} $
Selisih : $ \cos A - \cos B = -2 \sin \frac{1}{2}(A+B) \sin \frac{1}{2}(A-B) $
Sudut negatif : $ \sin (-x) = -\sin x $
$\spadesuit \, $ Meyederhanakan bentuk $ \cos x - \cos 3x $
$\begin{align} \cos A - \cos B & = -2 \sin \frac{1}{2}(A+B) \sin \frac{1}{2}(A-B) \\ \cos x - \cos 3x & = -2 \sin \frac{1}{2}(x+3x) \sin \frac{1}{2}(x-3x) \\ & = -2 \sin \frac{1}{2}(4x) \sin \frac{1}{2}(-2x) \\ & = -2 \sin 2x \sin (-x) \\ & = -2 \sin 2x . -\sin x \\ & = 2 \sin 2x \sin x \end{align}$
$\spadesuit \, $ Meyelesaikan soalnya
$\begin{align} & \displaystyle \lim_{x \to 0} \frac{x^2\sqrt{4-x^3}}{\cos x - \cos 3x} \\ & = \displaystyle \lim_{x \to 0} \frac{x^2\sqrt{4-x^3}}{2 \sin 2x \sin x } \\ & = \displaystyle \lim_{x \to 0} \frac{x}{ \sin 2x } . \frac{x}{\sin x } . \frac{\sqrt{4-x^3}}{2 } \\ & = \frac{1}{2} . \frac{1}{1} . \frac{\sqrt{4-0^3}}{2 } \\ & = \frac{1}{2}. \frac{1}{1} . \frac{2}{2 } = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Limit : $\displaystyle \lim_{x \to 0} \frac{ax}{\sin bx} = \frac{a}{b} $
Selisih : $ \cos A - \cos B = -2 \sin \frac{1}{2}(A+B) \sin \frac{1}{2}(A-B) $
Sudut negatif : $ \sin (-x) = -\sin x $
$\spadesuit \, $ Meyederhanakan bentuk $ \cos x - \cos 3x $
$\begin{align} \cos A - \cos B & = -2 \sin \frac{1}{2}(A+B) \sin \frac{1}{2}(A-B) \\ \cos x - \cos 3x & = -2 \sin \frac{1}{2}(x+3x) \sin \frac{1}{2}(x-3x) \\ & = -2 \sin \frac{1}{2}(4x) \sin \frac{1}{2}(-2x) \\ & = -2 \sin 2x \sin (-x) \\ & = -2 \sin 2x . -\sin x \\ & = 2 \sin 2x \sin x \end{align}$
$\spadesuit \, $ Meyelesaikan soalnya
$\begin{align} & \displaystyle \lim_{x \to 0} \frac{x^2\sqrt{4-x^3}}{\cos x - \cos 3x} \\ & = \displaystyle \lim_{x \to 0} \frac{x^2\sqrt{4-x^3}}{2 \sin 2x \sin x } \\ & = \displaystyle \lim_{x \to 0} \frac{x}{ \sin 2x } . \frac{x}{\sin x } . \frac{\sqrt{4-x^3}}{2 } \\ & = \frac{1}{2} . \frac{1}{1} . \frac{\sqrt{4-0^3}}{2 } \\ & = \frac{1}{2}. \frac{1}{1} . \frac{2}{2 } = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Nomor 5
Jumlah deret suatu geometri tak hingga dengan suku pertama $ a $ dan rasio $ r $ dengan $ 0 < r < 1 $ adalah S. Jika suku pertama
tetap dan rasio berubah menjadi ($1-r$), maka jumlahnya menjadi ....
$\clubsuit \, $ Diketahui : Rasio = $ r $ dengan $ 0 < r < 1 $ dan $ S_\infty = S $
Konsep : $ S_\infty = \frac{\text{Suku pertama}}{1-\text{rasio}} $
$\clubsuit \, $ Menentukan nilai $ a $ (suku pertama)
$\begin{align} S_\infty & = \frac{a}{1-r} \\ S & = \frac{a}{1-r} \rightarrow a = S(1-r) \end{align}$
$\clubsuit \, $ Suku pertama tetap (nilai $ a $ ) dan rasio berubah
(rasio = $1-r$ )
$\clubsuit \, $ Menentukan Jumlah tak hingga barunya
$\begin{align} S_\infty \, (\text{baru}) & = \frac{\text{Suku pertama}}{1-\text{rasio}} \\ & = \frac{a}{1-(1-r)} \\ & = \frac{S(1-r)}{r} \\ & = S(\frac{1}{r} - 1) \end{align}$
Jadi, jumlahnya menjadi $ S(\frac{1}{r} - 1) . \heartsuit$
Konsep : $ S_\infty = \frac{\text{Suku pertama}}{1-\text{rasio}} $
$\clubsuit \, $ Menentukan nilai $ a $ (suku pertama)
$\begin{align} S_\infty & = \frac{a}{1-r} \\ S & = \frac{a}{1-r} \rightarrow a = S(1-r) \end{align}$
$\clubsuit \, $ Suku pertama tetap (nilai $ a $ ) dan rasio berubah
(rasio = $1-r$ )
$\clubsuit \, $ Menentukan Jumlah tak hingga barunya
$\begin{align} S_\infty \, (\text{baru}) & = \frac{\text{Suku pertama}}{1-\text{rasio}} \\ & = \frac{a}{1-(1-r)} \\ & = \frac{S(1-r)}{r} \\ & = S(\frac{1}{r} - 1) \end{align}$
Jadi, jumlahnya menjadi $ S(\frac{1}{r} - 1) . \heartsuit$