Pembahasan soal SPMK UB Matematika IPA tahun 2009 ini agak ribet sobat, kenapa? karena soalnya menggunakan Petunjuk B dan Petunjuk C dalam menjawab soal, pasti dijamin panjang jawabannya karena harus diisi banyak alasan untuk setiap pernyataan.
Nomor 11
Petunjuk B digunakan untuk menjawab soal nomor 10 dan 11.
Sebuah kotak berisi 5 bola putih dan 6 bola hitam. Jika diambil 4 bola dari kotak tersebut, maka peluang terambilnya tepat 2 bola hitam pada pengambilan tersebut adalah $ \frac{5}{11} \, $ .
SEBAB
Banyaknya cara untuk mengambil 4 bola dari 11 bola dalam kotak adalah 330 cara.
Sebuah kotak berisi 5 bola putih dan 6 bola hitam. Jika diambil 4 bola dari kotak tersebut, maka peluang terambilnya tepat 2 bola hitam pada pengambilan tersebut adalah $ \frac{5}{11} \, $ .
SEBAB
Banyaknya cara untuk mengambil 4 bola dari 11 bola dalam kotak adalah 330 cara.
$\clubsuit \,$ ada 5P dan 6H, artinya total ada 11 bola . Pada kasus pengambilan bola menggunakan kombinasi karena
urutan tidak diperhatikan.
Konsep kombinasi : $ C_r^n = \frac{n!}{(n-r)!.r!} $
$\clubsuit \,$ diambil 4 bola dari 11 bola, total cara pengambilan :
$ n(S) = C_4^{11} = \frac{11!}{(11-4)!.4!} = \frac{11!}{7!.4!} = 330 $
$\clubsuit \,$ Harapannya terambil 2 bola hitam, karena harus terambil 4 bola maka sisanya harus terambil 2 bola putih. Sehingga harapannya terambil 2 bola putih dan 2 bola hitam. Total harapannya : $ n(A) = C_2^5.C_2^6 = 150 $
$\clubsuit \,$ Menentukan peluang terambil 2 hitam dan 2 putih
$ P(A) = \frac{n(A)}{n(S)} = \frac{150}{330} = \frac{5}{11} $
$\clubsuit \,$ Berdasarkan petunjuk B
*) Pernyataan pertama :
peluangnya = $ \frac{5}{11} \, $ (benar)
*) Pernyataan kedua :
banyak cara mengambil 4 bola dari 11 bola [ $n(S)$ ] adalah 330 cara. (benar)
karena kedua pernyataan benar dan ada hubungan sebab akibat, maka berdasarkan petunjuk B jawabannya adalah A.
Jadi, jawabannya A. $ \heartsuit $
Konsep kombinasi : $ C_r^n = \frac{n!}{(n-r)!.r!} $
$\clubsuit \,$ diambil 4 bola dari 11 bola, total cara pengambilan :
$ n(S) = C_4^{11} = \frac{11!}{(11-4)!.4!} = \frac{11!}{7!.4!} = 330 $
$\clubsuit \,$ Harapannya terambil 2 bola hitam, karena harus terambil 4 bola maka sisanya harus terambil 2 bola putih. Sehingga harapannya terambil 2 bola putih dan 2 bola hitam. Total harapannya : $ n(A) = C_2^5.C_2^6 = 150 $
$\clubsuit \,$ Menentukan peluang terambil 2 hitam dan 2 putih
$ P(A) = \frac{n(A)}{n(S)} = \frac{150}{330} = \frac{5}{11} $
$\clubsuit \,$ Berdasarkan petunjuk B
*) Pernyataan pertama :
peluangnya = $ \frac{5}{11} \, $ (benar)
*) Pernyataan kedua :
banyak cara mengambil 4 bola dari 11 bola [ $n(S)$ ] adalah 330 cara. (benar)
karena kedua pernyataan benar dan ada hubungan sebab akibat, maka berdasarkan petunjuk B jawabannya adalah A.
Jadi, jawabannya A. $ \heartsuit $
Nomor 12
Petunjuk C digunakan untuk menjawab soal nomor 12 sampai 15.
Diketahui $ f(x) = \int \limits_a^x t \, dt \, $ dengan $ a > 0 \, $ . Jika $ f(2)=0, \, $ maka kurva tersebut memotong sumbu X pada titik ....
(1). (-4,0) (2). (2,0) (3). (4,0) (4). (-2,0)
Diketahui $ f(x) = \int \limits_a^x t \, dt \, $ dengan $ a > 0 \, $ . Jika $ f(2)=0, \, $ maka kurva tersebut memotong sumbu X pada titik ....
(1). (-4,0) (2). (2,0) (3). (4,0) (4). (-2,0)
$\spadesuit \, $ Konsep integral : $ \int x^n dx = \frac{1}{n+1}x^{n+1} + c $
$\spadesuit \, $ Menentukan fungsi $ f(x) \, $ dan substitusi $ f(2) = 0 $
$\begin{align} f(x) & = \int \limits_a^x t \, dt \\ f(x) & = \frac{1}{2}t^2 |_a^x \\ f(x) & = \frac{1}{2}x^2 - \frac{1}{2}a^2 \\ f(2) & = 0 \\ \frac{1}{2}.2^2 - \frac{1}{2}a^2 & = 0 \\ a^2 & = 4 \rightarrow a = \pm 2 \end{align}$
karena $ a > 0, \, $ maka yang memenuhi adalah $ a = 2 \, $ , sehingga fungsinya menjadi :
$ f(x) = \frac{1}{2}x^2 - \frac{1}{2}a^2 \rightarrow f(x) = \frac{1}{2}x^2 - \frac{1}{2}.2^2 $
$ f(x) = \frac{1}{2}x^2 - 2 $
$\spadesuit \, $ Menentukan tipot sumbu X, substitusi $ y = 0 $
$\begin{align} y = 0 \rightarrow f(x) & = \frac{1}{2}x^2 - 2 \\ 0 & = \frac{1}{2}x^2 - 2 \\ x^2 & = 4 \\ x & = \pm 2 \end{align}$
artinya titik potong sumbu X adalah (2,0) dan (-2,0), sehingga yang benar adalah pernyataan (2) dan (4) yaitu opsi C.
Jadi, jawabannya adalah C. $ \heartsuit $
$\spadesuit \, $ Menentukan fungsi $ f(x) \, $ dan substitusi $ f(2) = 0 $
$\begin{align} f(x) & = \int \limits_a^x t \, dt \\ f(x) & = \frac{1}{2}t^2 |_a^x \\ f(x) & = \frac{1}{2}x^2 - \frac{1}{2}a^2 \\ f(2) & = 0 \\ \frac{1}{2}.2^2 - \frac{1}{2}a^2 & = 0 \\ a^2 & = 4 \rightarrow a = \pm 2 \end{align}$
karena $ a > 0, \, $ maka yang memenuhi adalah $ a = 2 \, $ , sehingga fungsinya menjadi :
$ f(x) = \frac{1}{2}x^2 - \frac{1}{2}a^2 \rightarrow f(x) = \frac{1}{2}x^2 - \frac{1}{2}.2^2 $
$ f(x) = \frac{1}{2}x^2 - 2 $
$\spadesuit \, $ Menentukan tipot sumbu X, substitusi $ y = 0 $
$\begin{align} y = 0 \rightarrow f(x) & = \frac{1}{2}x^2 - 2 \\ 0 & = \frac{1}{2}x^2 - 2 \\ x^2 & = 4 \\ x & = \pm 2 \end{align}$
artinya titik potong sumbu X adalah (2,0) dan (-2,0), sehingga yang benar adalah pernyataan (2) dan (4) yaitu opsi C.
Jadi, jawabannya adalah C. $ \heartsuit $
Nomor 13
Petunjuk C digunakan untuk menjawab soal nomor 12 sampai 15.
Jika $ p, \, q \, $ dan $ r \, $ bilangan bulat dan memenuhi $ p-2r=q(p-1) , \, $ maka pernyataan berikut yang benar adalah ....
(1). Jika $ q \neq 1 \, $ maka $ p(1-q)=2r-q $
(2). Jika $ q =0 \, $ dan $ p \neq 1 \, $ maka $ r=2 $
(3). Jika $ r = 1/2 \, $ dan $ p \neq 0 \, $ maka $ q=1 $
(4). Jika $ p \neq 2r \, $ maka $ q = 0 $
Jika $ p, \, q \, $ dan $ r \, $ bilangan bulat dan memenuhi $ p-2r=q(p-1) , \, $ maka pernyataan berikut yang benar adalah ....
(1). Jika $ q \neq 1 \, $ maka $ p(1-q)=2r-q $
(2). Jika $ q =0 \, $ dan $ p \neq 1 \, $ maka $ r=2 $
(3). Jika $ r = 1/2 \, $ dan $ p \neq 0 \, $ maka $ q=1 $
(4). Jika $ p \neq 2r \, $ maka $ q = 0 $
$\clubsuit \,$ Konsep logika matematika
*) $ p \Rightarrow q \, $ bernilai salah jika p bernilai benar (ruas kiri) dan q bernilai salah (ruas kanan), atau bentuknya $ B \Rightarrow S \, $ , ketarangan : B = Benar dan S = Salah.
*) $ p \Rightarrow q \, $ dibaca jika p maka q.
*) Dari pernyataan (1) sampai (4), kita anggap ruas kiri semuanya benar, sehingga kita tinggal cek ruas kanannya.
$\clubsuit \,$ Cek semua pernyataan
(1). Jika $ q \neq 1 \, $ maka $ p(1-q)=2r-q \, $
dapat ditulis : $ q \neq 1 \Rightarrow p(1-q)=2r-q $
$\begin{align} p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2r & = qp-q \\ p-qp & = 2r-q \\ p(1-q) & = 2r - q \end{align}$
untuk $ q \neq 1 \, $ , maka nilai $ 1-q \neq 0 \, $ , artinya $ p(1-q) = 2r - q \, $ (ruas kanan) bernilai benar. Karena ruas kanan benar, maka pernyataan (1) benar.
(2). Jika $ q =0 \, $ dan $ p \neq 1 \, $ maka $ r=2 $
dapat ditulis : $ (q= 0 \wedge p\neq 1) \Rightarrow r = 2 $
$\begin{align} q = 0 \rightarrow p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2r & = 0.(p-1) \\ p-2r & = 0 \\ r & = \frac{p}{2} \end{align}$
untuk $ p\neq 0 \, $ , maka nilai $ r = \frac{p}{2} \, $ nilainya tidak selalu $ r = 2 \, $ karena nilai $ p \, $ banyak sekali, ini artinya pernyataan (2) salah. catatan : kebenaran ini berlaku umum.
(3). Jika $ r = 1/2 \, $ dan $ p \neq 0 \, $ maka $ q=1 $
dapat ditulis : $ (r = 1/2 \wedge p \neq 0 ) \Rightarrow q = 1 $
$\begin{align} r = 1/2 \rightarrow p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2.\frac{1}{2} & = q(p-1) \\ p-1 & = q(p-1) \\ q & = \frac{p-1}{p-1} = 1 \end{align}$
artinya $ q = 1 \, $ (ruas kanan) bernilai benar, sehingga pernyataan (3) benar.
(4). Jika $ p \neq 2r \, $ maka $ q = 0 $
dapat ditulis : $ p \neq 2r \Rightarrow q = 0 $
$\begin{align} p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ q & = \frac{p-2r}{p-1} \end{align}$
nilai $ q = 0 \, $ diperoleh jika nilai $ p = 2r \, $ , artinya jika $ p\neq 2r \, $ maka nilai $ q \neq 0 \, $ (ruas kanan salah). Sehingga pernyataan (4) salah.
Jadi, pernyataan yang benar adalah (1) dan (3) , sehingga jawabannya B . $ \heartsuit $
*) $ p \Rightarrow q \, $ bernilai salah jika p bernilai benar (ruas kiri) dan q bernilai salah (ruas kanan), atau bentuknya $ B \Rightarrow S \, $ , ketarangan : B = Benar dan S = Salah.
*) $ p \Rightarrow q \, $ dibaca jika p maka q.
*) Dari pernyataan (1) sampai (4), kita anggap ruas kiri semuanya benar, sehingga kita tinggal cek ruas kanannya.
$\clubsuit \,$ Cek semua pernyataan
(1). Jika $ q \neq 1 \, $ maka $ p(1-q)=2r-q \, $
dapat ditulis : $ q \neq 1 \Rightarrow p(1-q)=2r-q $
$\begin{align} p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2r & = qp-q \\ p-qp & = 2r-q \\ p(1-q) & = 2r - q \end{align}$
untuk $ q \neq 1 \, $ , maka nilai $ 1-q \neq 0 \, $ , artinya $ p(1-q) = 2r - q \, $ (ruas kanan) bernilai benar. Karena ruas kanan benar, maka pernyataan (1) benar.
(2). Jika $ q =0 \, $ dan $ p \neq 1 \, $ maka $ r=2 $
dapat ditulis : $ (q= 0 \wedge p\neq 1) \Rightarrow r = 2 $
$\begin{align} q = 0 \rightarrow p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2r & = 0.(p-1) \\ p-2r & = 0 \\ r & = \frac{p}{2} \end{align}$
untuk $ p\neq 0 \, $ , maka nilai $ r = \frac{p}{2} \, $ nilainya tidak selalu $ r = 2 \, $ karena nilai $ p \, $ banyak sekali, ini artinya pernyataan (2) salah. catatan : kebenaran ini berlaku umum.
(3). Jika $ r = 1/2 \, $ dan $ p \neq 0 \, $ maka $ q=1 $
dapat ditulis : $ (r = 1/2 \wedge p \neq 0 ) \Rightarrow q = 1 $
$\begin{align} r = 1/2 \rightarrow p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ p-2.\frac{1}{2} & = q(p-1) \\ p-1 & = q(p-1) \\ q & = \frac{p-1}{p-1} = 1 \end{align}$
artinya $ q = 1 \, $ (ruas kanan) bernilai benar, sehingga pernyataan (3) benar.
(4). Jika $ p \neq 2r \, $ maka $ q = 0 $
dapat ditulis : $ p \neq 2r \Rightarrow q = 0 $
$\begin{align} p-2r & = q(p-1) \, \, \, \, \text{(persamaan awal)} \\ q & = \frac{p-2r}{p-1} \end{align}$
nilai $ q = 0 \, $ diperoleh jika nilai $ p = 2r \, $ , artinya jika $ p\neq 2r \, $ maka nilai $ q \neq 0 \, $ (ruas kanan salah). Sehingga pernyataan (4) salah.
Jadi, pernyataan yang benar adalah (1) dan (3) , sehingga jawabannya B . $ \heartsuit $
Nomor 14
Petunjuk C digunakan untuk menjawab soal nomor 12 sampai 15.
Diketahui pernyataan $ p \, $ dan $ q . \, $ Pernyataan berikut yang dapat bernilai salah adalah ....
(1). $ ( p \wedge q ) \Rightarrow p $
(2). $ ( p \wedge q ) \Rightarrow q $
(3). $ q \Rightarrow ( p \vee q ) $
(4). $ ( p \vee q ) \Rightarrow p $
Diketahui pernyataan $ p \, $ dan $ q . \, $ Pernyataan berikut yang dapat bernilai salah adalah ....
(1). $ ( p \wedge q ) \Rightarrow p $
(2). $ ( p \wedge q ) \Rightarrow q $
(3). $ q \Rightarrow ( p \vee q ) $
(4). $ ( p \vee q ) \Rightarrow p $
$\spadesuit \, $ Tabel kebenaran logika matematika

Keterangan : B = Benar dan S = Salah
Dari tabel dapat disimpulkan bahwa implikasi $(\Rightarrow) \, $ akan bernilai salah jika ruas kiri bernilai benar (B) dan ruas kanan bernilai salah (S) atau bentuknya $ B \Rightarrow S $ . Sehingga patokannya ruas kanan dulu harus bernilai salah (S) kemudian ruas kiri bernilai benar (B).
$\spadesuit \, $ Kita cek semua pernyataan apakah benar atau salah
(1). $ ( p \wedge q ) \Rightarrow p $
Pilih nilai p = S (ruas kanan) , maka otomatis nilai $ ( p \wedge q ) = \, $ S (ruas kiri), sehingga $ ( p \wedge q ) \Rightarrow p \equiv S \Rightarrow S \, $ (bernilai benar). Artinya pernyataan (1) benar.
(2). $ ( p \wedge q ) \Rightarrow q $
Pernyataan (2) juga benar karena mirip dengan pernyataan (1).
(3). $ q \Rightarrow ( p \vee q ) $
pilih nilai p = S dan q = S agar nilai $ ( p \vee q ) \, $ = S (ruas kanan), sehingga $ q \Rightarrow ( p \vee q ) \equiv S \Rightarrow S \, $ (bernilai benar). Artinya pernyataan (3) benar.
(4). $ ( p \vee q ) \Rightarrow p $
Pilih nilai p = S (ruas kanan) dan q = B , maka $ ( p \vee q ) \, $ = B (ruas kiri), sehingga $ ( p \vee q ) \Rightarrow p \equiv B \Rightarrow S \, $ (bernilai salah). artinya pernyataan (4) bisa salah.
Jadi, pernyataan yang benar (tidak salah) adalah (1), (2), dan (3), sehingga jawabannya A. $ \heartsuit $

Keterangan : B = Benar dan S = Salah
Dari tabel dapat disimpulkan bahwa implikasi $(\Rightarrow) \, $ akan bernilai salah jika ruas kiri bernilai benar (B) dan ruas kanan bernilai salah (S) atau bentuknya $ B \Rightarrow S $ . Sehingga patokannya ruas kanan dulu harus bernilai salah (S) kemudian ruas kiri bernilai benar (B).
$\spadesuit \, $ Kita cek semua pernyataan apakah benar atau salah
(1). $ ( p \wedge q ) \Rightarrow p $
Pilih nilai p = S (ruas kanan) , maka otomatis nilai $ ( p \wedge q ) = \, $ S (ruas kiri), sehingga $ ( p \wedge q ) \Rightarrow p \equiv S \Rightarrow S \, $ (bernilai benar). Artinya pernyataan (1) benar.
(2). $ ( p \wedge q ) \Rightarrow q $
Pernyataan (2) juga benar karena mirip dengan pernyataan (1).
(3). $ q \Rightarrow ( p \vee q ) $
pilih nilai p = S dan q = S agar nilai $ ( p \vee q ) \, $ = S (ruas kanan), sehingga $ q \Rightarrow ( p \vee q ) \equiv S \Rightarrow S \, $ (bernilai benar). Artinya pernyataan (3) benar.
(4). $ ( p \vee q ) \Rightarrow p $
Pilih nilai p = S (ruas kanan) dan q = B , maka $ ( p \vee q ) \, $ = B (ruas kiri), sehingga $ ( p \vee q ) \Rightarrow p \equiv B \Rightarrow S \, $ (bernilai salah). artinya pernyataan (4) bisa salah.
Jadi, pernyataan yang benar (tidak salah) adalah (1), (2), dan (3), sehingga jawabannya A. $ \heartsuit $
Nomor 15
Petunjuk C digunakan untuk menjawab soal nomor 12 sampai 15.
Diketahui fungsi $ f(x)=\frac{2}{3}x^3 + 4x^2 - 10x \, $. Pernyataan yang benar untuk fungsi tersebut adalah ....
(1). Mempunyai nilai maksimum lokal di $ x = -5 \, $ dan minimum lokal di $ x = 1 $
(2). Mempunyai titik belok di $ x= -2 $
(3). Turun pada interval $ -5 < x < 1 $
(4). Melewati titik (0,0)
Diketahui fungsi $ f(x)=\frac{2}{3}x^3 + 4x^2 - 10x \, $. Pernyataan yang benar untuk fungsi tersebut adalah ....
(1). Mempunyai nilai maksimum lokal di $ x = -5 \, $ dan minimum lokal di $ x = 1 $
(2). Mempunyai titik belok di $ x= -2 $
(3). Turun pada interval $ -5 < x < 1 $
(4). Melewati titik (0,0)
$\clubsuit \,$ konsep turunan
$ f^\prime (x) = 0 \rightarrow \, $ nilai maksimum/minimum
$ f^\prime (x) > 0 \rightarrow \, $ fungsi naik
$ f^\prime (x) < 0 \rightarrow \, $ fungsi turun
$ f^{\prime \prime } (x) = 0 \rightarrow \, $ titik belok
$\clubsuit \,$ Menentukan turunan fungsinya
$\begin{align} f(x) & =\frac{2}{3}x^3 + 4x^2 - 10x \\ f^\prime (x) & = 2x^2 + 8x - 10 \\ f^{\prime \prime} (x) & = 4x + 8 \end{align}$
$\clubsuit \,$ Menentukan nilai maksimum/minimum : $ f^\prime (x) = 0 $
$\begin{align} f^\prime (x) & = 0 \\ 2x^2 + 8x - 10 & = 0 \, \, \, \, \text{(bagi 2)} \\ x^2 + 4x - 5 & = 0 \\ (x-1)(x+5) & = 0 \\ x = 1 \vee x & = - 5 \end{align}$
Garis bilangan turunannya :
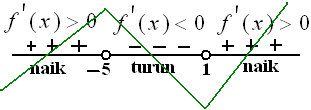
keterangan :
*) Fungsi $ f(x) \, $ maksimum lokal di $ x = -5 \, $ dan minimum lokal di $ x = 1 $ . artinya pernyataan (1) benar.
*) Fungsi turun pada interval $ -5 < x < 1 \, $
artinya pernyataan (3) benar.
$\clubsuit \,$ Menentukan titik belok : $ f^{\prime \prime } (x) = 0 $
$\begin{align} f^{\prime \prime} (x) & = 0 \rightarrow 4x + 8 = 0 \rightarrow x = -2 \end{align}$
artinya $ f(x) \, $ mempunyai titik belok di $ x = -2 \, $ , pernyataan (2) benar.
$\clubsuit \,$ Substitusi $ x =0 \, $ ke fungsi
$\begin{align} x =0 \rightarrow f(x) & = \frac{2}{3}x^3 + 4x^2 - 10x \\ f(0) & = \frac{2}{3}.0^3 + 4.0^2 - 10.0 = 0 \end{align}$
artinya fungsi $ f(x) \, $ melewati titik (0,0), pernyataan (4) benar.
Jadi, semua pernyataan benar, sehingga jawabannya E. $ \heartsuit $
$ f^\prime (x) = 0 \rightarrow \, $ nilai maksimum/minimum
$ f^\prime (x) > 0 \rightarrow \, $ fungsi naik
$ f^\prime (x) < 0 \rightarrow \, $ fungsi turun
$ f^{\prime \prime } (x) = 0 \rightarrow \, $ titik belok
$\clubsuit \,$ Menentukan turunan fungsinya
$\begin{align} f(x) & =\frac{2}{3}x^3 + 4x^2 - 10x \\ f^\prime (x) & = 2x^2 + 8x - 10 \\ f^{\prime \prime} (x) & = 4x + 8 \end{align}$
$\clubsuit \,$ Menentukan nilai maksimum/minimum : $ f^\prime (x) = 0 $
$\begin{align} f^\prime (x) & = 0 \\ 2x^2 + 8x - 10 & = 0 \, \, \, \, \text{(bagi 2)} \\ x^2 + 4x - 5 & = 0 \\ (x-1)(x+5) & = 0 \\ x = 1 \vee x & = - 5 \end{align}$
Garis bilangan turunannya :

keterangan :
*) Fungsi $ f(x) \, $ maksimum lokal di $ x = -5 \, $ dan minimum lokal di $ x = 1 $ . artinya pernyataan (1) benar.
*) Fungsi turun pada interval $ -5 < x < 1 \, $
artinya pernyataan (3) benar.
$\clubsuit \,$ Menentukan titik belok : $ f^{\prime \prime } (x) = 0 $
$\begin{align} f^{\prime \prime} (x) & = 0 \rightarrow 4x + 8 = 0 \rightarrow x = -2 \end{align}$
artinya $ f(x) \, $ mempunyai titik belok di $ x = -2 \, $ , pernyataan (2) benar.
$\clubsuit \,$ Substitusi $ x =0 \, $ ke fungsi
$\begin{align} x =0 \rightarrow f(x) & = \frac{2}{3}x^3 + 4x^2 - 10x \\ f(0) & = \frac{2}{3}.0^3 + 4.0^2 - 10.0 = 0 \end{align}$
artinya fungsi $ f(x) \, $ melewati titik (0,0), pernyataan (4) benar.
Jadi, semua pernyataan benar, sehingga jawabannya E. $ \heartsuit $