Nomor 11
Jika $ A = \left[ \begin{matrix} 2 & 1 \\ a & 4 \end{matrix} \right] \, $
merupakan matriks yang mempunyai invers dan $ det(B) = 4 , \, $ maka hasil kali semua nilai $ a \, $ yang mungkin sehingga
$ det(A) = 16 det \left( (AB)^{-1} \right) \, $
adalah .....
$\spadesuit \, $ sifat-sifat determinan
$ |A^{-1}| = \frac{1}{|A|} \, $ dan $ |A.B | = |A|.|B| $
$\spadesuit \, $ Menentukan nilai determinan A
$ A = \left[ \begin{matrix} 2 & 1 \\ a & 4 \end{matrix} \right] $
$ det(A) = |A| = 2.4 - a.1 = 8 - a $
Diketahui juga : $ det(B) = |B| = 4 $
$\spadesuit \, $ Menentukan nilai $ a $
$\begin{align} det(A) & = 16 det \left( (AB)^{-1} \right) \\ |A| & = 16 | (AB)^{-1} | \\ |A| & = 16 . \frac{1}{|AB|} \\ |A| & = \frac{16}{|A|.|B|} \\ |A|^2 & = \frac{16}{|B|} \\ (8-a)^2 & = \frac{16}{4} \\ (8-a)^2 & = 4 \\ 64-16a + a^2 & = 4 \\ a^2 -16a + 60 & = 0 \\ (a-6)(a-10) & = 0 \\ a_1=6 \vee a_2 & = 10 \end{align}$
hasil kali nilai $ a \, $ adalah $ a_1.a_2 = 6.10 = 60 $
atau gunakan operasi akar-akar :
$ a^2 -16a + 60 = 0 \rightarrow a_1.a_2 = \frac{c}{a} = \frac{60}{1} = 60 $
Jadi, hasil kali semua nilai $ a \, $ adalah 60. $ \heartsuit $
$ |A^{-1}| = \frac{1}{|A|} \, $ dan $ |A.B | = |A|.|B| $
$\spadesuit \, $ Menentukan nilai determinan A
$ A = \left[ \begin{matrix} 2 & 1 \\ a & 4 \end{matrix} \right] $
$ det(A) = |A| = 2.4 - a.1 = 8 - a $
Diketahui juga : $ det(B) = |B| = 4 $
$\spadesuit \, $ Menentukan nilai $ a $
$\begin{align} det(A) & = 16 det \left( (AB)^{-1} \right) \\ |A| & = 16 | (AB)^{-1} | \\ |A| & = 16 . \frac{1}{|AB|} \\ |A| & = \frac{16}{|A|.|B|} \\ |A|^2 & = \frac{16}{|B|} \\ (8-a)^2 & = \frac{16}{4} \\ (8-a)^2 & = 4 \\ 64-16a + a^2 & = 4 \\ a^2 -16a + 60 & = 0 \\ (a-6)(a-10) & = 0 \\ a_1=6 \vee a_2 & = 10 \end{align}$
hasil kali nilai $ a \, $ adalah $ a_1.a_2 = 6.10 = 60 $
atau gunakan operasi akar-akar :
$ a^2 -16a + 60 = 0 \rightarrow a_1.a_2 = \frac{c}{a} = \frac{60}{1} = 60 $
Jadi, hasil kali semua nilai $ a \, $ adalah 60. $ \heartsuit $
Nomor 12
Jika akar-akar $ x^2 - ax -b = 0 \, $ saling berkebalikan dan salah satu akar tersebut merupakan bilangan bulat positif, maka nilai
terkecil yang mungkin untuk $ a - b \, $ adalah ....
$\clubsuit \, $ Akar-akar berkebalikan
Misalkan akar-akar PK $ x^2 - ax - b = 0 \, $ adalah $ x_1 \, $ dan $ x_2, \, $ karena saling berkebalikan, maka haruslah $ x_2 = \frac{1}{x_1} \, $ . Sehingga $ x_1 . x_2 = x_1 . \frac{1}{x_1} = 1 \, $ dengan $ x_1 \, $ sebagai akar bulat positif.
$\clubsuit \, $ Operasi akar-akar PK : $ x^2 -ax-b=0 $
$ x_1 + x_2 = \frac{-(-a)}{1} = a \rightarrow x_1 + \frac{1}{x_1} = a \, $ ....pers(i)
$ x_1 . x_2 = \frac{-b}{1} \rightarrow 1 = -b \rightarrow b = -1 \, $ ....pers(ii)
$\clubsuit \, $ Menentukan hasilnya
$ a - b = (x_1 + \frac{1}{x_1}) - (-1) $
$ a - b = x_1 + \frac{1}{x_1} + 1 \, $ ....pers(iii)
*). Agar nilai $ a - b \, $ sekecil mungkin, maka nilai $ x_1 \, $ harus sekecil mungkin. Karena $ x_1 \, $ adalah akar bulat positif, maka nilai terkecilnya adalah $ x_1 = 1 . $
Diperoleh :
$ a-b = x_1 + \frac{1}{x_1} + 1 = 1 + \frac{1}{1} + 1 = 3 $
Jadi, nilai terkecil yang mungkin untuk $ a - b \, $ adalah 3. $ \heartsuit $
Misalkan akar-akar PK $ x^2 - ax - b = 0 \, $ adalah $ x_1 \, $ dan $ x_2, \, $ karena saling berkebalikan, maka haruslah $ x_2 = \frac{1}{x_1} \, $ . Sehingga $ x_1 . x_2 = x_1 . \frac{1}{x_1} = 1 \, $ dengan $ x_1 \, $ sebagai akar bulat positif.
$\clubsuit \, $ Operasi akar-akar PK : $ x^2 -ax-b=0 $
$ x_1 + x_2 = \frac{-(-a)}{1} = a \rightarrow x_1 + \frac{1}{x_1} = a \, $ ....pers(i)
$ x_1 . x_2 = \frac{-b}{1} \rightarrow 1 = -b \rightarrow b = -1 \, $ ....pers(ii)
$\clubsuit \, $ Menentukan hasilnya
$ a - b = (x_1 + \frac{1}{x_1}) - (-1) $
$ a - b = x_1 + \frac{1}{x_1} + 1 \, $ ....pers(iii)
*). Agar nilai $ a - b \, $ sekecil mungkin, maka nilai $ x_1 \, $ harus sekecil mungkin. Karena $ x_1 \, $ adalah akar bulat positif, maka nilai terkecilnya adalah $ x_1 = 1 . $
Diperoleh :
$ a-b = x_1 + \frac{1}{x_1} + 1 = 1 + \frac{1}{1} + 1 = 3 $
Jadi, nilai terkecil yang mungkin untuk $ a - b \, $ adalah 3. $ \heartsuit $
Nomor 13
Jika grafik fungsi $ y = x^2 - 9 \, $ memotong sumbu x di titik A dan B, serta memotong sumbu y di titik C, maka luas segitiga
ABC adalah ....
$\spadesuit \, $ Menentukan titik potong sumbu-sumbu
*) Titik potong sumbu y : substitusi $ x = 0 $
$\begin{align} y & = x^2 - 9 \\ y & = 0^2 - 9 \\ y & = - 9 \end{align}$
artinya titik C(0,-9)
*) Titik potong sumbu x : substitusi $ y = 0 $
$\begin{align} y & = x^2 - 9 \\ 0 & = x^2 - 9 \\ x^2 & = 9 \\ x & = \pm \sqrt{9} = \pm 3 \end{align}$
artinya titik A(-3,0) dan B(3,0)
$\spadesuit \, $ gambar segitiganya
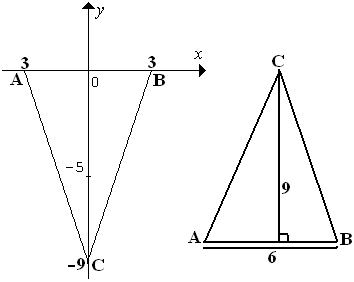
$\spadesuit \, $ Menentukan luas segitiganya
$\begin{align} L_{\Delta ABC} & = \frac{1}{2}.a.t = \frac{1}{2}.6.9= 27 \end{align}$
Jadi, luas segitiganya adalah 27. $ \heartsuit $
*) Titik potong sumbu y : substitusi $ x = 0 $
$\begin{align} y & = x^2 - 9 \\ y & = 0^2 - 9 \\ y & = - 9 \end{align}$
artinya titik C(0,-9)
*) Titik potong sumbu x : substitusi $ y = 0 $
$\begin{align} y & = x^2 - 9 \\ 0 & = x^2 - 9 \\ x^2 & = 9 \\ x & = \pm \sqrt{9} = \pm 3 \end{align}$
artinya titik A(-3,0) dan B(3,0)
$\spadesuit \, $ gambar segitiganya

$\spadesuit \, $ Menentukan luas segitiganya
$\begin{align} L_{\Delta ABC} & = \frac{1}{2}.a.t = \frac{1}{2}.6.9= 27 \end{align}$
Jadi, luas segitiganya adalah 27. $ \heartsuit $
Nomor 14
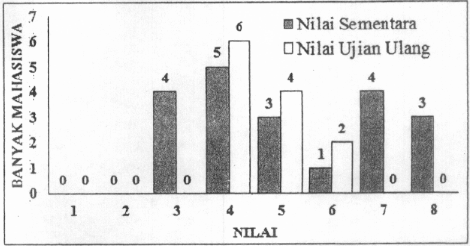
Nilai semua tes matematika dinyatakan dengan bilangan bulat dari 0 sampai 10. Median terkecil yang mungkin bagi siswa yang memiliki
rata-rata nilai 6 dari enam kali tes adalah ....
$\clubsuit \,$ Konsep rata-rata : $ \overline{X} = \frac{\text{Jumlah semua data}}{\text{banyak data}} $
$\clubsuit \, $ Misalkan datanya : $ x_1, x_2, x_3, x_4, x_5 x_6 \, $ yang telah diurutkan dari kecil ke besar dengan rata-ratanya 6, sehingga diperoleh :
$\begin{align} \overline{X} & = 6 \\ \frac{x_1+x_2+x_3+x_4+x_5+x_6}{6} & = 6 \\ x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \, \, \, \, \text{ ...pers(i)} \end{align} $
Sementara nilai mediannya : $ Me = \frac{x_3+x_4}{2} $
$\clubsuit \,$ Analisa nilai data yang mungkin
*). Agar mediannya sekecil mungkin, maka nilai $ x_3 \, $ dan $ x_4 \, $ juga harus terkecil.
*). Agar $ x_3 \, $ dan $ x_4 \, $ terkecil, maka nilai $ x_5 \, $ dan $ x_6 \, $ harus terbesar, dengan nilai $ x_5 = 10 \, $ dan $ x_6 = 10. $
$\begin{align} x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \\ x_1+x_2+x_3+x_4+10+10 & = 36 \\ x_1+x_2+x_3+x_4& = 16 \, \, \, \, \text{ ...pers(ii)} \end{align} $
*). karena nilai $ x_1 \leq x_2 \leq x_3 \leq x_4 , \, $ maka dari pers(ii) diperoleh nilai $ x_1 = 4, x_2=4, x_3=4,x_4=4 \, \, \, $ yang menyebabkan nilai $ x_3 \, $ dan $ x_4 \, $ terkecil.
Sehingga : $ Me = \frac{x_3+x_4}{2} = \frac{4+4}{2} = 4 $
Jadi, nilai median terkecilnya adalah 4. $ \heartsuit $
$\clubsuit \, $ Misalkan datanya : $ x_1, x_2, x_3, x_4, x_5 x_6 \, $ yang telah diurutkan dari kecil ke besar dengan rata-ratanya 6, sehingga diperoleh :
$\begin{align} \overline{X} & = 6 \\ \frac{x_1+x_2+x_3+x_4+x_5+x_6}{6} & = 6 \\ x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \, \, \, \, \text{ ...pers(i)} \end{align} $
Sementara nilai mediannya : $ Me = \frac{x_3+x_4}{2} $
$\clubsuit \,$ Analisa nilai data yang mungkin
*). Agar mediannya sekecil mungkin, maka nilai $ x_3 \, $ dan $ x_4 \, $ juga harus terkecil.
*). Agar $ x_3 \, $ dan $ x_4 \, $ terkecil, maka nilai $ x_5 \, $ dan $ x_6 \, $ harus terbesar, dengan nilai $ x_5 = 10 \, $ dan $ x_6 = 10. $
$\begin{align} x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \\ x_1+x_2+x_3+x_4+10+10 & = 36 \\ x_1+x_2+x_3+x_4& = 16 \, \, \, \, \text{ ...pers(ii)} \end{align} $
*). karena nilai $ x_1 \leq x_2 \leq x_3 \leq x_4 , \, $ maka dari pers(ii) diperoleh nilai $ x_1 = 4, x_2=4, x_3=4,x_4=4 \, \, \, $ yang menyebabkan nilai $ x_3 \, $ dan $ x_4 \, $ terkecil.
Sehingga : $ Me = \frac{x_3+x_4}{2} = \frac{4+4}{2} = 4 $
Jadi, nilai median terkecilnya adalah 4. $ \heartsuit $
Nomor 15
Empat buku berjudul Matematika, satu buku berjudul Ekonomi, dan satu buku berjudul Bahasa akan disusun di lemari buku dalam satu baris.
Misalkan A adalah kejadian susunan buku sehingga tidak ada tiga atau lebih buku dengan judul yang sama tersusun secara berurutan.
Jika buku dengan judul yang sama tidak dibedakan, maka peluang kejadian A adalah .....
$\spadesuit \, $ Pada kasus ini menggunakan Permutasi Berulang.
Misalkan kata "BAHAGIA" akan disusun ulang, maka banyaknya kata baru (tidak harus bermakna) yang diperoleh adalah $\frac{\text{total huruf}}{\text{huruf yang sama}} = \frac{7!}{3!} = 7 \times 6 \times 5 \times 4 \, $ kata, di sini huruf yang sama hanya huruf A sebanyak 3.
Contoh lain, kata "MATEMATIKA" disusun ulang, kata baru sebanyak $ \frac{10!}{2!\times 3! \times 2!} \, $ kata (total huruf = 10, yang sama : M = 2, A = 3, T = 2).
$\spadesuit \, $ Misal : M = Matematika, E = Ekonomi, B = Bahasa
Ada 4M 1E 1B , artinya $ n(S) = \frac{6!}{4!} = 6.5 = 30 $
$ n(S) \, $ adalah ruang sampel (semua susunan yang mungkin)
$\spadesuit \, $ Kejadian A menyatakan kejadian susunan buku sehingga tidak ada tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Agar kejadian ini terjadi, salah satu caranya adalah kita blok menjadi lima bagian buku dengan dua kemungkinan.
*). Kemungkinan I :
KI = $ 2!.\frac{3!}{2!} = 3! = 3.2.1 = 6 $
*). Kemungkinan II :
KII = $ 2!.\frac{3!}{2!} = 3! = 3.2.1 = 6 \, $
Hanya saja susunan MMEBMM dan MMBEMM sudah muncul pada kemungikan I, sehinga harus dikurangkan 2 : KII = 6 - 2 = 4 cara.
*). Kemungkinan III , 2M ada ditengah yaitu : MEMMBM dan MBMMEM
diperoleh KIII = 2
Sehingga semua kemungkinan kejadian A :
$ n(A) = KI + KII + KIII = 6 + 4 + 2 = 12 $
$\spadesuit \, $ Menentukan peluangnya
$ P(A) = \frac{n(A)}{n(S)} = \frac{12}{30} = \frac{2}{5} $
Jadi, peluang kejadian A adalah $ \frac{2}{5}. \heartsuit $
Keterangan kemungkinan yang ada :
Kemungkinan I :

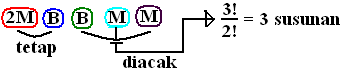
*). Kita bagi menjadi 5 kelompok yaitu 2M, E, B, M, dan M dengan 2M posisinya pasti tetap di depan.
*). Tiga kelompok terakhir (B, M, M) kita acak posisinya dengan banyak susunan $ \frac{3!}{2!} = 3 \, $ cara.
*). E dan B bisa saling ditukar, sehingga susunannya ada 2! = 2 cara.
Sehingga semua susunan kemungkinan I ada $ \frac{3!}{2!} \times 2! = 3 \times 2 = 6 \, $ cara yaitu MMEBMM, MMEMBM, MMEMMB, MMBEMM, MMBMEM, dan MMBMME
Hal yang sama juga untuk kemungkinan II, hanya saja 2M posisinya tetap dibelakang.
Misalkan kata "BAHAGIA" akan disusun ulang, maka banyaknya kata baru (tidak harus bermakna) yang diperoleh adalah $\frac{\text{total huruf}}{\text{huruf yang sama}} = \frac{7!}{3!} = 7 \times 6 \times 5 \times 4 \, $ kata, di sini huruf yang sama hanya huruf A sebanyak 3.
Contoh lain, kata "MATEMATIKA" disusun ulang, kata baru sebanyak $ \frac{10!}{2!\times 3! \times 2!} \, $ kata (total huruf = 10, yang sama : M = 2, A = 3, T = 2).
$\spadesuit \, $ Misal : M = Matematika, E = Ekonomi, B = Bahasa
Ada 4M 1E 1B , artinya $ n(S) = \frac{6!}{4!} = 6.5 = 30 $
$ n(S) \, $ adalah ruang sampel (semua susunan yang mungkin)
$\spadesuit \, $ Kejadian A menyatakan kejadian susunan buku sehingga tidak ada tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Agar kejadian ini terjadi, salah satu caranya adalah kita blok menjadi lima bagian buku dengan dua kemungkinan.
*). Kemungkinan I :

KI = $ 2!.\frac{3!}{2!} = 3! = 3.2.1 = 6 $
*). Kemungkinan II :

KII = $ 2!.\frac{3!}{2!} = 3! = 3.2.1 = 6 \, $
Hanya saja susunan MMEBMM dan MMBEMM sudah muncul pada kemungikan I, sehinga harus dikurangkan 2 : KII = 6 - 2 = 4 cara.
*). Kemungkinan III , 2M ada ditengah yaitu : MEMMBM dan MBMMEM
diperoleh KIII = 2
Sehingga semua kemungkinan kejadian A :
$ n(A) = KI + KII + KIII = 6 + 4 + 2 = 12 $
$\spadesuit \, $ Menentukan peluangnya
$ P(A) = \frac{n(A)}{n(S)} = \frac{12}{30} = \frac{2}{5} $
Jadi, peluang kejadian A adalah $ \frac{2}{5}. \heartsuit $
Keterangan kemungkinan yang ada :
Kemungkinan I :

*). Kita bagi menjadi 5 kelompok yaitu 2M, E, B, M, dan M dengan 2M posisinya pasti tetap di depan.
*). Tiga kelompok terakhir (B, M, M) kita acak posisinya dengan banyak susunan $ \frac{3!}{2!} = 3 \, $ cara.
*). E dan B bisa saling ditukar, sehingga susunannya ada 2! = 2 cara.
Sehingga semua susunan kemungkinan I ada $ \frac{3!}{2!} \times 2! = 3 \times 2 = 6 \, $ cara yaitu MMEBMM, MMEMBM, MMEMMB, MMBEMM, MMBMEM, dan MMBMME
Hal yang sama juga untuk kemungkinan II, hanya saja 2M posisinya tetap dibelakang.