Nomor 21
Diberikan persamaan :
$\left( \sqrt[3]{\frac{1}{243}} \right)^{3x} = \left( \frac{3}{3^{x-2}} \right)^2 . \sqrt[3]{\frac{1}{9}} $ .
Jika $ x_0 $ memenuhi persamaan, maka nilai $ 1- \frac{3}{4}x_0 = .... $
$\left( \sqrt[3]{\frac{1}{243}} \right)^{3x} = \left( \frac{3}{3^{x-2}} \right)^2 . \sqrt[3]{\frac{1}{9}} $ .
Jika $ x_0 $ memenuhi persamaan, maka nilai $ 1- \frac{3}{4}x_0 = .... $
$\spadesuit \, $ Menentukan nilai $ x $
$\begin{align} \left( \sqrt[3]{\frac{1}{243}} \right)^{3x} & = \left( \frac{3}{3^{x-2}} \right)^2 . \sqrt[3]{\frac{1}{9}} \\ \left( 3^{-5} \right)^{\frac{3x}{x}} & = \left( 3^{1-(x-2)} \right)^2 . (3^{-2})^\frac{1}{3} \\ (3)^{-5x} & = \left( 3^{-x+3} \right)^2 . (3)^\frac{-2}{3} \\ (3)^{-5x} & = 3^{-2x+6} . (3)^\frac{-2}{3} \\ 3^{-5x} & = 3^{-2x+6+(\frac{-2}{3})} \\ 3^{-5x} & = 3^{-2x+\frac{16}{3}} \\ -5x & = -2x+\frac{16}{3} \\ -3x & = \frac{16}{3} \rightarrow x_0 = -\frac{16}{9} \end{align}$
Sehingga nilai :
$1- \frac{3}{4}x_0 = 1 - \frac{3}{4}. (-\frac{16}{9}) = 1 + \frac{4}{3} = 2\frac{1}{3} $
Jadi, nilai $ 1- \frac{3}{4}x_0 = 2\frac{1}{3} . \heartsuit $
$\begin{align} \left( \sqrt[3]{\frac{1}{243}} \right)^{3x} & = \left( \frac{3}{3^{x-2}} \right)^2 . \sqrt[3]{\frac{1}{9}} \\ \left( 3^{-5} \right)^{\frac{3x}{x}} & = \left( 3^{1-(x-2)} \right)^2 . (3^{-2})^\frac{1}{3} \\ (3)^{-5x} & = \left( 3^{-x+3} \right)^2 . (3)^\frac{-2}{3} \\ (3)^{-5x} & = 3^{-2x+6} . (3)^\frac{-2}{3} \\ 3^{-5x} & = 3^{-2x+6+(\frac{-2}{3})} \\ 3^{-5x} & = 3^{-2x+\frac{16}{3}} \\ -5x & = -2x+\frac{16}{3} \\ -3x & = \frac{16}{3} \rightarrow x_0 = -\frac{16}{9} \end{align}$
Sehingga nilai :
$1- \frac{3}{4}x_0 = 1 - \frac{3}{4}. (-\frac{16}{9}) = 1 + \frac{4}{3} = 2\frac{1}{3} $
Jadi, nilai $ 1- \frac{3}{4}x_0 = 2\frac{1}{3} . \heartsuit $
Nomor 22
Sebuah bola pingpong dijatuhkan kelantai dari ketinggian 2 meter. Setiap kali setiap bola itu memantul ia mencapai ketinggian tiga per empat
dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola tersebut dari pantulan ke-3 sampai berhenti adalah ....
$\clubsuit \, $ Gambar
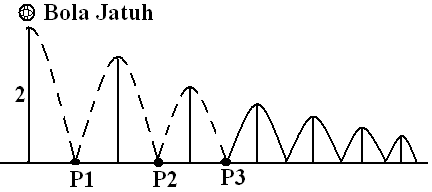
Pantulan awal dari pantulan ke-3 (suku ke-4) dengan $ a = 2, r = \frac{3}{4} $
$\clubsuit \, $ Menentkan panajang lintasan menggunakan deret tak hingga
Panjang lintasan dihitung dari setelah pantulan ke-3 (garis penuh). Karena lintasan naik dan turun panjangnya sama, serta bola berhenti sampai pantulan tak hingga, maka panjang lintasan (PL) :
$\begin{align} PL & = 2. S_\infty \\ PL & = 2. \frac{Suku pertama}{1-r} \\ & = 2. \frac{U_4}{1-r} \\ & = 2. \frac{ar^3}{1-r} \\ & = 2. \frac{2.(\frac{3}{4})^3}{1-\frac{3}{4}} \\ & = \frac{27}{4} = 6,75 \end{align}$
Jadi, panjang lintasannya adalah 6,75 m . $ \heartsuit $

Pantulan awal dari pantulan ke-3 (suku ke-4) dengan $ a = 2, r = \frac{3}{4} $
$\clubsuit \, $ Menentkan panajang lintasan menggunakan deret tak hingga
Panjang lintasan dihitung dari setelah pantulan ke-3 (garis penuh). Karena lintasan naik dan turun panjangnya sama, serta bola berhenti sampai pantulan tak hingga, maka panjang lintasan (PL) :
$\begin{align} PL & = 2. S_\infty \\ PL & = 2. \frac{Suku pertama}{1-r} \\ & = 2. \frac{U_4}{1-r} \\ & = 2. \frac{ar^3}{1-r} \\ & = 2. \frac{2.(\frac{3}{4})^3}{1-\frac{3}{4}} \\ & = \frac{27}{4} = 6,75 \end{align}$
Jadi, panjang lintasannya adalah 6,75 m . $ \heartsuit $
Nomor 23
Jumlah 5 suku pertama sebuah deret geometri adalah -33. Jika nilai pembandingnya adalah -2, maka jumlah nilai suku ke-3 dan ke-4 deret ini adalah ....
$\spadesuit \, $ Barisan Geometri : $ U_n = ar^{n-1} \, $ dan $ \, S_n = \frac{a(r^n-1)}{r-1} $
$\spadesuit \, $ Menentukan nilai $ a $ dengan $ S_5=-33, \, r = -2 $
$\begin{align} S_5 = -3 \rightarrow \frac{a((-2)^5-1)}{-2-1} & = -33 \\ \frac{a(-32-1)}{-3} & = -33 \\ \frac{a(-33)}{-3} & = -33 \\ a & = -3 \end{align}$
$\spadesuit \, $ Menentukan nilai $ U_3 $ dan $ U_4 $
$ U_3 = ar^2 = -3(-2)^2 = -12 $
$ U_4 = ar^3 = -3(-2)^3 = 24 $
Sehingga : $ U_3+U_4 = -12 + 24 = 12 $
Jadi, nilai $U_3+U_4 = 12 . \heartsuit $
$\spadesuit \, $ Menentukan nilai $ a $ dengan $ S_5=-33, \, r = -2 $
$\begin{align} S_5 = -3 \rightarrow \frac{a((-2)^5-1)}{-2-1} & = -33 \\ \frac{a(-32-1)}{-3} & = -33 \\ \frac{a(-33)}{-3} & = -33 \\ a & = -3 \end{align}$
$\spadesuit \, $ Menentukan nilai $ U_3 $ dan $ U_4 $
$ U_3 = ar^2 = -3(-2)^2 = -12 $
$ U_4 = ar^3 = -3(-2)^3 = 24 $
Sehingga : $ U_3+U_4 = -12 + 24 = 12 $
Jadi, nilai $U_3+U_4 = 12 . \heartsuit $
Nomor 24
Suku ke-6 sebuah deret aritmetika adalah 24.000 dan suku ke-10 adalah 18.000. Supaya suku ke-$n$ sama dengan 0, maka nilai $n$ adalah ....
$\clubsuit \,$ Barisan aritmetika : $ U_n = a + (n-1)b $
$\clubsuit \,$ Menentukan nilai $ a $ dan $ b $
$\begin{array}{ccc} U_6=24000 \rightarrow & a + 5 b = 24000 & \\ U_{10} = 18000 \rightarrow & a+9b = 18000 & - \\ \hline & -4b = 6000 & \\ & b = -1500 & \end{array} $
pers(i) : $ a + 5b=24000 \rightarrow a+5(-1500) = 24000 \rightarrow a = 31500 $
$\clubsuit \,$ Menentukan nilai $ n $ dengan $ U_n = 0 $
$\begin{align} U_n & = 0 \\ a + (n-1)b & = 0 \\ 31500 + (n-1).(-1500) & = 0 \\ 31500 -1500n + 1500 & = 0 \\ 1500n & = 33000 \\ n & = \frac{33000}{1500} = 22 \end{align}$
Jadi, nilai $ n = 22 . \heartsuit $
$\clubsuit \,$ Menentukan nilai $ a $ dan $ b $
$\begin{array}{ccc} U_6=24000 \rightarrow & a + 5 b = 24000 & \\ U_{10} = 18000 \rightarrow & a+9b = 18000 & - \\ \hline & -4b = 6000 & \\ & b = -1500 & \end{array} $
pers(i) : $ a + 5b=24000 \rightarrow a+5(-1500) = 24000 \rightarrow a = 31500 $
$\clubsuit \,$ Menentukan nilai $ n $ dengan $ U_n = 0 $
$\begin{align} U_n & = 0 \\ a + (n-1)b & = 0 \\ 31500 + (n-1).(-1500) & = 0 \\ 31500 -1500n + 1500 & = 0 \\ 1500n & = 33000 \\ n & = \frac{33000}{1500} = 22 \end{align}$
Jadi, nilai $ n = 22 . \heartsuit $
Nomor 25
Diketahui $ B = \left( \begin{matrix} 3 & 1 \\ 2 & 0 \end{matrix} \right) $ dan $ C = \left( \begin{matrix} 0 & 2 \\ 3 & 6 \end{matrix} \right) $ .
Determinan dari matriks $ B.C $ adalah K . Jika garis $ 2x-y = 5 $ dan $ x+y=1 $ berpotongan di titik A, maka persamaan garis
yang melalui A dan bergradien K adalah ....
$\spadesuit \, $ Konsep Determinan : $|A.B| = |A|.|B| $
$\spadesuit \, $ Menentukan nilai $K$
$\begin{align} K & = |B.C| = |B|.|C| \\ K & = \left| \begin{matrix} 3 & 1 \\ 2 & 0 \end{matrix} \right|. \left| \begin{matrix} 0 & 2 \\ 3 & 6 \end{matrix} \right| \\ & = (3.0 - 2.1) . (0.6 - 3.2) \\ & = -2 . (-6) = 12 \end{align}$
$\spadesuit \, $ Menentukan titik A dengan eliminasi
$\begin{array}{cc} 2x-y = 5 & \\ x + y = 1 & + \\ \hline 3x = 6 & \\ x = 2 & \end{array}$
pers(ii) : $ x+y = 1 \rightarrow 2 + y = 1 \rightarrow y = -1 $
Sehingga titik A(2,-1)
$\spadesuit \, $ Persamaan garis melalu ($x_1,y_1$) = (2,-1) dan gradien $ m = K = 12 $
$\begin{align} y-y_1 & = m (x-x_1) \\ y + 1 & = 12(x-2) \\ y+1 & = 12x - 24 \\ y -12x+25 & = 0 \end{align}$
Jadi, persamaan garis lurusnya adalah $ y -12x+25 = 0 . \heartsuit $
$\spadesuit \, $ Menentukan nilai $K$
$\begin{align} K & = |B.C| = |B|.|C| \\ K & = \left| \begin{matrix} 3 & 1 \\ 2 & 0 \end{matrix} \right|. \left| \begin{matrix} 0 & 2 \\ 3 & 6 \end{matrix} \right| \\ & = (3.0 - 2.1) . (0.6 - 3.2) \\ & = -2 . (-6) = 12 \end{align}$
$\spadesuit \, $ Menentukan titik A dengan eliminasi
$\begin{array}{cc} 2x-y = 5 & \\ x + y = 1 & + \\ \hline 3x = 6 & \\ x = 2 & \end{array}$
pers(ii) : $ x+y = 1 \rightarrow 2 + y = 1 \rightarrow y = -1 $
Sehingga titik A(2,-1)
$\spadesuit \, $ Persamaan garis melalu ($x_1,y_1$) = (2,-1) dan gradien $ m = K = 12 $
$\begin{align} y-y_1 & = m (x-x_1) \\ y + 1 & = 12(x-2) \\ y+1 & = 12x - 24 \\ y -12x+25 & = 0 \end{align}$
Jadi, persamaan garis lurusnya adalah $ y -12x+25 = 0 . \heartsuit $




