Nomor 6
Diketahui vektor satuan $ \vec{u} = 0,8\vec{i} + a \vec{j}. \, $ Jika vektor $ \vec{v} = b\vec{i} + \vec{j} \, $
tegak lurus $ \vec{u} \, $ , maka $ a . b = .... $
$\spadesuit \, $ Konsep dasar
Panjang vektor $ \vec{u} = a\vec{i} + b \vec{j} \rightarrow \text{panjang } = | \vec{u}| = \sqrt{a^2+b^2} $
$ \vec{u} \, $ vektor satuan, sehingga $ | \vec{u} | = 1 $
$ \vec{u} \, $ tegak lurus $ \vec{v} \, $ , sehingga $ \vec{u}. \vec{v} = 0 $
$\spadesuit \, $ Menentukan nilai $ a $
$ \vec{u} = 0,8\vec{i} + a \vec{j} \, $ vektor satuan, sehingga
$\begin{align} | \vec{u} | = 1 \rightarrow \sqrt{(0,8)^2 + a^2 } & = 1 \\ 0,64 + a^2 & = 1 \\ a^2 & = 0,36 \\ a & = 0,6 \end{align}$
$\spadesuit \, $ Menentukan nilai $ b $
$ \vec{u} \, $ tegak lurus $ \vec{v} \, $ sehingga $ \vec{u}. \vec{v} = 0 $
dengan $ \vec{u} = 0,8\vec{i} + a \vec{j} \, $ dan $ \vec{v} = b\vec{i} + \vec{j} $
$\begin{align} \vec{u}. \vec{v} & = 0 \\ 0,8 . b + a.1 & = 0 \\ 0,8b + 0,6 . 1 & = 0 \\ 0,8b & = -0,6 \rightarrow b = \frac{-0,6}{0,8} = -\frac{3}{4} \end{align}$
Sehingga nilai $ a . b = (0,6) . (-\frac{3}{4}) = (\frac{3}{5}) . (-\frac{3}{4} ) = -\frac{9}{20} $
Jadi, nilai $ a . b = -\frac{9}{20} . \heartsuit $
Panjang vektor $ \vec{u} = a\vec{i} + b \vec{j} \rightarrow \text{panjang } = | \vec{u}| = \sqrt{a^2+b^2} $
$ \vec{u} \, $ vektor satuan, sehingga $ | \vec{u} | = 1 $
$ \vec{u} \, $ tegak lurus $ \vec{v} \, $ , sehingga $ \vec{u}. \vec{v} = 0 $
$\spadesuit \, $ Menentukan nilai $ a $
$ \vec{u} = 0,8\vec{i} + a \vec{j} \, $ vektor satuan, sehingga
$\begin{align} | \vec{u} | = 1 \rightarrow \sqrt{(0,8)^2 + a^2 } & = 1 \\ 0,64 + a^2 & = 1 \\ a^2 & = 0,36 \\ a & = 0,6 \end{align}$
$\spadesuit \, $ Menentukan nilai $ b $
$ \vec{u} \, $ tegak lurus $ \vec{v} \, $ sehingga $ \vec{u}. \vec{v} = 0 $
dengan $ \vec{u} = 0,8\vec{i} + a \vec{j} \, $ dan $ \vec{v} = b\vec{i} + \vec{j} $
$\begin{align} \vec{u}. \vec{v} & = 0 \\ 0,8 . b + a.1 & = 0 \\ 0,8b + 0,6 . 1 & = 0 \\ 0,8b & = -0,6 \rightarrow b = \frac{-0,6}{0,8} = -\frac{3}{4} \end{align}$
Sehingga nilai $ a . b = (0,6) . (-\frac{3}{4}) = (\frac{3}{5}) . (-\frac{3}{4} ) = -\frac{9}{20} $
Jadi, nilai $ a . b = -\frac{9}{20} . \heartsuit $
Nomor 7
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2. Jika P titik tengah HG, Q titik tengah FG, R titik tengah PQ, dan BS
adalah proyeksi BR pada bidang ABCD, maka panjang BS adalah .....
$\clubsuit \, $ Gambar

Proyeksi BR pada ABCD adalah BS.
$ BM = \frac{1}{2}BD = \frac{1}{2}. 2\sqrt{2} = \sqrt{2} $
$ MS = \frac{1}{2} MC = \frac{1}{2} \sqrt{2} $
$\clubsuit \, $ Menentukan panjang BS pada $\Delta$BMS
$\begin{align} BS & = \sqrt{BM^2 + MS^2 } = \sqrt{ (\sqrt{2})^2 + (\frac{1}{2} \sqrt{2} )^2 } \\ & = \sqrt{ 4 + \frac{1}{2} } = \sqrt{ \frac{5}{2} } \\ & = \frac{\sqrt{5}}{\sqrt{2}} . \frac{\sqrt{2}}{\sqrt{2}} \\ & = \frac{1}{2} \sqrt{10} \end{align}$
Jadi, panjang $ BS = \frac{1}{2} \sqrt{10} . \heartsuit$

Proyeksi BR pada ABCD adalah BS.
$ BM = \frac{1}{2}BD = \frac{1}{2}. 2\sqrt{2} = \sqrt{2} $
$ MS = \frac{1}{2} MC = \frac{1}{2} \sqrt{2} $
$\clubsuit \, $ Menentukan panjang BS pada $\Delta$BMS
$\begin{align} BS & = \sqrt{BM^2 + MS^2 } = \sqrt{ (\sqrt{2})^2 + (\frac{1}{2} \sqrt{2} )^2 } \\ & = \sqrt{ 4 + \frac{1}{2} } = \sqrt{ \frac{5}{2} } \\ & = \frac{\sqrt{5}}{\sqrt{2}} . \frac{\sqrt{2}}{\sqrt{2}} \\ & = \frac{1}{2} \sqrt{10} \end{align}$
Jadi, panjang $ BS = \frac{1}{2} \sqrt{10} . \heartsuit$
Nomor 8
Jika lingkaran $ x^2 + y^2 + 6x + 6y + c = 0 \, $ menyinggung garis $ x = 2, \, $
maka nilai $ c $ adalah .....
$\spadesuit \, $ Substitusi $ x = 2 \, $ ke persamaan lingkaran
$\begin{align} x = 2 \rightarrow x^2 + y^2 + 6x + 6y + c & = 0 \\ 2^2 + y^2 + 6.2 + 6y + c & = 0 \\ y^2 + 6y + (c + 16) & = 0 \end{align}$
Syarat Menyinggung : $ D = 0 $
$\begin{align} b^2 - 4ac & = 0 \\ 6^2 - 4. 1. (c + 16) & = 0 \\ 36 - 4c - 64 & = 0 \\ 4c & = -28 \\ c & = -7 \end{align}$
Jadi, nilai $ c = -7 . \heartsuit$
$\begin{align} x = 2 \rightarrow x^2 + y^2 + 6x + 6y + c & = 0 \\ 2^2 + y^2 + 6.2 + 6y + c & = 0 \\ y^2 + 6y + (c + 16) & = 0 \end{align}$
Syarat Menyinggung : $ D = 0 $
$\begin{align} b^2 - 4ac & = 0 \\ 6^2 - 4. 1. (c + 16) & = 0 \\ 36 - 4c - 64 & = 0 \\ 4c & = -28 \\ c & = -7 \end{align}$
Jadi, nilai $ c = -7 . \heartsuit$
Nomor 9
Himpunan penyelesaian $ |x^2 - 2 | \leq 1 \, $ adalah himpunan nilai $ x $ yang memenuhi .....
$\clubsuit \, $ Konsep dasar : $ |x|^2 = x^2 \, $ dan $ p^2 - q^2 = (p-q)(p+q) $
$\clubsuit \, $ Kuadratkan kedua ruas
$\begin{align} |x^2 - 2 |^2 & \leq 1^2 \\ (x^2 - 2 )^2 & \leq 1^2 \\ (x^2 - 2 )^2 - 1^2 & \leq 0 \\ [x^2 - 2 - 1 ][x^2 - 2 + 1 ] & \leq 0 \\ (x^2-3)(x^2 - 1) & \leq 0 \\ x^2 - 3 = 0 \rightarrow x^2 & = 3 \rightarrow x = \pm \sqrt{3} \\ x^2 - 1 = 0 \rightarrow x^2 & = 1 \rightarrow x = \pm 1 \end{align}$
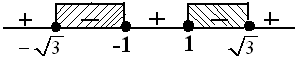
Jadi, solusinya $ HP = \{ -\sqrt{3} \leq x \leq -1 \vee 1 \leq x \leq \sqrt{3} \} . \heartsuit $
$\clubsuit \, $ Kuadratkan kedua ruas
$\begin{align} |x^2 - 2 |^2 & \leq 1^2 \\ (x^2 - 2 )^2 & \leq 1^2 \\ (x^2 - 2 )^2 - 1^2 & \leq 0 \\ [x^2 - 2 - 1 ][x^2 - 2 + 1 ] & \leq 0 \\ (x^2-3)(x^2 - 1) & \leq 0 \\ x^2 - 3 = 0 \rightarrow x^2 & = 3 \rightarrow x = \pm \sqrt{3} \\ x^2 - 1 = 0 \rightarrow x^2 & = 1 \rightarrow x = \pm 1 \end{align}$
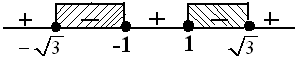
Jadi, solusinya $ HP = \{ -\sqrt{3} \leq x \leq -1 \vee 1 \leq x \leq \sqrt{3} \} . \heartsuit $
Nomor 10
$ \displaystyle \lim_{ x \to 1 } \frac{(x^2+x-2) \sin (x-1)}{x^2 - 2x + 1} = ..... $
$\spadesuit \, $ Konsep dasar limit
$ \displaystyle \lim_{ x \to k } \frac{ \sin a f(x) }{b f(x)} = \frac{a}{b} \, $ dengan syarat $ \, f(k) = 0 $
$\spadesuit \, $ Menyelesaikan limitnya
$\begin{align} & \displaystyle \lim_{ x \to 1 } \frac{(x^2+x-2) \sin (x-1)}{x^2 - 2x + 1} \\ & = \displaystyle \lim_{ x \to 1 } \frac{(x+2)(x-1) \sin (x-1)}{(x-1)(x-1)} \\ & = \displaystyle \lim_{ x \to 1 } \frac{(x+2) \sin (x-1)}{(x-1)} \\ & = \displaystyle \lim_{ x \to 1 } (x+2) . \frac{ \sin (x-1)}{(x-1)} \\ & = (1+2) . \frac{1}{1} = 3 \end{align}$
Jadi, nilai limitnya adalah 3. $ \heartsuit $
$ \displaystyle \lim_{ x \to k } \frac{ \sin a f(x) }{b f(x)} = \frac{a}{b} \, $ dengan syarat $ \, f(k) = 0 $
$\spadesuit \, $ Menyelesaikan limitnya
$\begin{align} & \displaystyle \lim_{ x \to 1 } \frac{(x^2+x-2) \sin (x-1)}{x^2 - 2x + 1} \\ & = \displaystyle \lim_{ x \to 1 } \frac{(x+2)(x-1) \sin (x-1)}{(x-1)(x-1)} \\ & = \displaystyle \lim_{ x \to 1 } \frac{(x+2) \sin (x-1)}{(x-1)} \\ & = \displaystyle \lim_{ x \to 1 } (x+2) . \frac{ \sin (x-1)}{(x-1)} \\ & = (1+2) . \frac{1}{1} = 3 \end{align}$
Jadi, nilai limitnya adalah 3. $ \heartsuit $