Nomor 6
Luas daerah yang dibatasi oleh garis $ y = x-1 \, $ dan parabola $ y^2 = 2x + 6 \, $ adalah .... satuan.
$\spadesuit \, $ gambar
$ y = x-1 \rightarrow x = y+1 $
$ y^2 = 2x + 6 \rightarrow x = \frac{1}{2}y^2 - 3 $
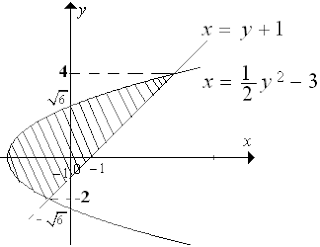
Titik potong kedua kurva :
$\begin{align} x_1 & = x_2 \\ \frac{1}{2}y^2 - 3 & = y + 1 \, \, \, \, \text{(kalii 2)} \\ y^2 -6 & = 2y + 2 \\ y^2 - 2y -8 & = 0 \\ (y-4)(y+2) & = 0 \\ y=4 \vee y & = -2 \end{align}$
$\spadesuit \, $ Menentukan luas daerah arsiran
$\begin{align} L & = \int \limits_{-2}^4 \text{ (kurva kanan)} - \text{ (kurva kiri)} dy \\ L & = \int \limits_{-2}^4 (y+1) - (\frac{1}{2}y^2 - 3) dy \\ L & = \int \limits_{-2}^4 ( -\frac{1}{2}y^2 + y + 4 ) \, dy \\ L & = ( -\frac{1}{6}y^3 + \frac{1}{2}y^2 + 4y )|_{-2}^4 \\ L & = ( -\frac{1}{6}.4^3 + \frac{1}{2}.4^2 + 4.4 ) - \\ & ( -\frac{1}{6}.(-2)^3 + \frac{1}{2}.(-2)^2 + 4.(-2) ) \\ L & = ( -\frac{32}{3} + 8 + 16 ) - ( \frac{4}{3} + 2 + -8 ) \\ L & = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $
$ y = x-1 \rightarrow x = y+1 $
$ y^2 = 2x + 6 \rightarrow x = \frac{1}{2}y^2 - 3 $

Titik potong kedua kurva :
$\begin{align} x_1 & = x_2 \\ \frac{1}{2}y^2 - 3 & = y + 1 \, \, \, \, \text{(kalii 2)} \\ y^2 -6 & = 2y + 2 \\ y^2 - 2y -8 & = 0 \\ (y-4)(y+2) & = 0 \\ y=4 \vee y & = -2 \end{align}$
$\spadesuit \, $ Menentukan luas daerah arsiran
$\begin{align} L & = \int \limits_{-2}^4 \text{ (kurva kanan)} - \text{ (kurva kiri)} dy \\ L & = \int \limits_{-2}^4 (y+1) - (\frac{1}{2}y^2 - 3) dy \\ L & = \int \limits_{-2}^4 ( -\frac{1}{2}y^2 + y + 4 ) \, dy \\ L & = ( -\frac{1}{6}y^3 + \frac{1}{2}y^2 + 4y )|_{-2}^4 \\ L & = ( -\frac{1}{6}.4^3 + \frac{1}{2}.4^2 + 4.4 ) - \\ & ( -\frac{1}{6}.(-2)^3 + \frac{1}{2}.(-2)^2 + 4.(-2) ) \\ L & = ( -\frac{32}{3} + 8 + 16 ) - ( \frac{4}{3} + 2 + -8 ) \\ L & = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $
Cara II :
$\spadesuit \, $ Luas daerah tertutup yang dibatasi oleh dua kurva (garis dengan parabola atau parabola dengan parabola) adalah $ L = \frac{D\sqrt{D}}{6a^2} \, $ dengan $ D = b^2-4ac $
$\spadesuit \, $ Substitusi garis ke parabola
$\begin{align} y & = x - 1 \rightarrow x = y+1 \\ y^2 & = 2x + 6 \rightarrow x = \frac{1}{2} y^2 - 3 \\ \frac{1}{2} y^2 - 3 & = y+1 \\ \frac{1}{2} y^2 -y -4 & = 0 \rightarrow a = \frac{1}{2}, \, b = -1, \, c = -4 \\ D & = b^2 - 4ac \\ D & = (-1)^2 - 4.(\frac{1}{2}).(-4) = 1 + 8 = 9 \\ L & = \frac{D\sqrt{D}}{6a^2} = \frac{9\sqrt{9}}{6.(\frac{1}{2})^2} = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $
$\spadesuit \, $ Luas daerah tertutup yang dibatasi oleh dua kurva (garis dengan parabola atau parabola dengan parabola) adalah $ L = \frac{D\sqrt{D}}{6a^2} \, $ dengan $ D = b^2-4ac $
$\spadesuit \, $ Substitusi garis ke parabola
$\begin{align} y & = x - 1 \rightarrow x = y+1 \\ y^2 & = 2x + 6 \rightarrow x = \frac{1}{2} y^2 - 3 \\ \frac{1}{2} y^2 - 3 & = y+1 \\ \frac{1}{2} y^2 -y -4 & = 0 \rightarrow a = \frac{1}{2}, \, b = -1, \, c = -4 \\ D & = b^2 - 4ac \\ D & = (-1)^2 - 4.(\frac{1}{2}).(-4) = 1 + 8 = 9 \\ L & = \frac{D\sqrt{D}}{6a^2} = \frac{9\sqrt{9}}{6.(\frac{1}{2})^2} = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $
Nomor 7
$ \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} = ..... $
Cara I : Menggunakan turunan
$\clubsuit \,$ Penerapan turunan pada limit
$ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \, $ solusinya $ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to k } \frac{f^\prime (x)}{g^\prime (x)} \, $ diturunkan sampai hasilnya tidak $ \frac{0}{0} $
Turunan akar : $ y = \sqrt{f(x)} \rightarrow y^\prime = \frac{f^\prime (x)}{2\sqrt{f(x)}} $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\frac{1}{2\sqrt{x}} - 1}{1-2x} \\ & = \frac{\frac{1}{2\sqrt{1}} - 1}{1-2.1} \\ & = \frac{\frac{1}{2} - 1}{1-2} = \frac{-\frac{1}{2}}{-1} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
$\clubsuit \,$ Penerapan turunan pada limit
$ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \, $ solusinya $ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to k } \frac{f^\prime (x)}{g^\prime (x)} \, $ diturunkan sampai hasilnya tidak $ \frac{0}{0} $
Turunan akar : $ y = \sqrt{f(x)} \rightarrow y^\prime = \frac{f^\prime (x)}{2\sqrt{f(x)}} $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\frac{1}{2\sqrt{x}} - 1}{1-2x} \\ & = \frac{\frac{1}{2\sqrt{1}} - 1}{1-2.1} \\ & = \frac{\frac{1}{2} - 1}{1-2} = \frac{-\frac{1}{2}}{-1} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Cara II : Merasionalkan bentuk akar
$\clubsuit \,$ Konsep kali sekawan
$ (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) = (\sqrt{p})^2-(\sqrt{q})^2 = p-q $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} . \frac{\sqrt{x} + x}{\sqrt{x} + x} \\ & = \displaystyle \lim_{x \to 1 } \frac{(x-x^2)}{(x-x^2)(\sqrt{x} + x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{1}{(\sqrt{x} + x)} \\ & = \frac{1}{(\sqrt{1} + 1)} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
$\clubsuit \,$ Konsep kali sekawan
$ (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) = (\sqrt{p})^2-(\sqrt{q})^2 = p-q $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} . \frac{\sqrt{x} + x}{\sqrt{x} + x} \\ & = \displaystyle \lim_{x \to 1 } \frac{(x-x^2)}{(x-x^2)(\sqrt{x} + x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{1}{(\sqrt{x} + x)} \\ & = \frac{1}{(\sqrt{1} + 1)} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Cara III : Pemfaktoran
$\clubsuit \,$ Konsep pemfaktoran : $ p-q = (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-\sqrt{x})(1+\sqrt{x})} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}}{x(1+\sqrt{x})} \\ & = \frac{\sqrt{1}}{1.(1+\sqrt{1})} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
$\clubsuit \,$ Konsep pemfaktoran : $ p-q = (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-\sqrt{x})(1+\sqrt{x})} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}}{x(1+\sqrt{x})} \\ & = \frac{\sqrt{1}}{1.(1+\sqrt{1})} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Nomor 8
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jika nilai terkecil dan terbesar dari fungsi $ f(x) = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \, $ adalah $ a \, $ dan $ b \, $ ,
maka nilai $ a + b = 6 $
SEBAB
$ a = -5 \, $ dan $ b = 11 . $
Jika nilai terkecil dan terbesar dari fungsi $ f(x) = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \, $ adalah $ a \, $ dan $ b \, $ ,
maka nilai $ a + b = 6 $
SEBAB
$ a = -5 \, $ dan $ b = 11 . $
$\spadesuit \, $ Konsep dasar trigonometri
*) $ \cos A \cos B = \frac{1}{2} [\cos (A+B) + \cos (A-B) ] $
*) Nilai maksimum/minimum dari : $ f(x) = P\cos g(x) + c \, $
$ f_\text{maks} = |P| + c \, $ dan $ f_\text{min} = -|P| + c $
$\spadesuit \, $ Menyederhanakan soalnya
Misal : $ A = \left( x - \frac{\pi}{4} \right) \, $ dan $ B = \left( x + \frac{\pi}{4} \right) $
$ A + B = \left( x - \frac{\pi}{4} \right) + \left( x + \frac{\pi}{4} \right) = 2x $
$ A - B = \left( x - \frac{\pi}{4} \right) - \left( x + \frac{\pi}{4} \right) = \frac{-\pi}{2} $
Substitusi nilai $ A \, $ dan $ B \, $ pada fungsinya :
$\begin{align} f(x) & = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \\ f(x) & = 8 \cos A \cos B + 3 \\ f(x) & = 8 .\frac{1}{2} . [\cos (A+B) + \cos (A-B) ] + 3 \\ f(x) & = 4 [\cos (2x) + \cos (\frac{-\pi}{2}) ] + 3 \\ f(x) & = 4 [\cos (2x) + 0 ] + 3 \\ f(x) & = 4 \cos (2x) + 3 \end{align}$
$\spadesuit \, $ Menentukan nilai maksimum dan minimum fungsi
$\begin{align} f(x) & = 4 \cos (2x) + 3 \rightarrow P = 4 , \, c = 3 \\ a & = f_\text{maks} = |P| + c = |4| + 3 = 4+3 = 7 \\ b & = f_\text{min} = -|P| + c = -|4| + 3 = -4+3 = -1 \end{align}$
Sehingga nilai : $ a +b = 7 + (-1) = 6 $
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : $ a + b = 6 \, $ (benar)
Pernyataan kedua : $ a = -5 , \, b = 11 \, $ (salah , karena seharusnya $ a = 7, \, b=-1$)
Karena pernyataan pertama benar dan pernyataan kedua salah, berdasarkan petunjuk B jawabannya adalah C.
Jadi, jawabannya C. $ \heartsuit $
*) $ \cos A \cos B = \frac{1}{2} [\cos (A+B) + \cos (A-B) ] $
*) Nilai maksimum/minimum dari : $ f(x) = P\cos g(x) + c \, $
$ f_\text{maks} = |P| + c \, $ dan $ f_\text{min} = -|P| + c $
$\spadesuit \, $ Menyederhanakan soalnya
Misal : $ A = \left( x - \frac{\pi}{4} \right) \, $ dan $ B = \left( x + \frac{\pi}{4} \right) $
$ A + B = \left( x - \frac{\pi}{4} \right) + \left( x + \frac{\pi}{4} \right) = 2x $
$ A - B = \left( x - \frac{\pi}{4} \right) - \left( x + \frac{\pi}{4} \right) = \frac{-\pi}{2} $
Substitusi nilai $ A \, $ dan $ B \, $ pada fungsinya :
$\begin{align} f(x) & = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \\ f(x) & = 8 \cos A \cos B + 3 \\ f(x) & = 8 .\frac{1}{2} . [\cos (A+B) + \cos (A-B) ] + 3 \\ f(x) & = 4 [\cos (2x) + \cos (\frac{-\pi}{2}) ] + 3 \\ f(x) & = 4 [\cos (2x) + 0 ] + 3 \\ f(x) & = 4 \cos (2x) + 3 \end{align}$
$\spadesuit \, $ Menentukan nilai maksimum dan minimum fungsi
$\begin{align} f(x) & = 4 \cos (2x) + 3 \rightarrow P = 4 , \, c = 3 \\ a & = f_\text{maks} = |P| + c = |4| + 3 = 4+3 = 7 \\ b & = f_\text{min} = -|P| + c = -|4| + 3 = -4+3 = -1 \end{align}$
Sehingga nilai : $ a +b = 7 + (-1) = 6 $
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : $ a + b = 6 \, $ (benar)
Pernyataan kedua : $ a = -5 , \, b = 11 \, $ (salah , karena seharusnya $ a = 7, \, b=-1$)
Karena pernyataan pertama benar dan pernyataan kedua salah, berdasarkan petunjuk B jawabannya adalah C.
Jadi, jawabannya C. $ \heartsuit $
Nomor 9
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jumlah $ n \, $ suku pertama suatu deret aritmetika dinyatakan dengan $ s_n = 2n^2 - n \, $ . Suku ke-12 deret tersebut adalah 45.
SEBAB
Deret tersebut mempunyai suku pertama $ a = 1 \, $ dan beda $ b = 4 . $
Jumlah $ n \, $ suku pertama suatu deret aritmetika dinyatakan dengan $ s_n = 2n^2 - n \, $ . Suku ke-12 deret tersebut adalah 45.
SEBAB
Deret tersebut mempunyai suku pertama $ a = 1 \, $ dan beda $ b = 4 . $
$\clubsuit \,$ Konsep Dasar Barisan aritmetika
$ u_n = a+(n-1)b, \, \, u_n = s_n - s_{n-1} , \, $ dan $ b = u_n - u_{n-1} $
$\clubsuit \,$ Menentukan nilai $ a \, $ dan $ b $
$\begin{align} s_n & = 2n^2 - n \\ a & = u_1 = s_1 = 2.1^2 - 1 = 1 \\ u_2 & = s_2 - s_1 \\ u_2 & = (2.2^2 - 2) - 1 = 6 - 1 = 5 \\ b & = u_2 - u_1 = 5 - 1 = 4 \end{align}$
sehingga nilai $ a = 1 \, $ dan $ b = 4 $
$\clubsuit \,$ Menentukan suku ke-12
$\begin{align} u_n & = a+(n-1)b \\ u_{12} & = 1+(12-1).4 \\ u_{12} & = 1+44 \\ u_{12} & = 45 \end{align}$
sehingga nilai $ u_{12} = 45 $
$\clubsuit \,$ Berdasarkan petunjuk B
Pernyataan pertama : $ u_{12} = 45 \, $ (benar)
Pernyataan kedua : $ a = 1 \, $ dan $ b = 4 \, $ (benar)
Karena kedua pernyataan benar dan saling berhubungan, maka berdasarkan petunjuk B jawabannya A.
Jadi, jawabannya A. $ \heartsuit $
$ u_n = a+(n-1)b, \, \, u_n = s_n - s_{n-1} , \, $ dan $ b = u_n - u_{n-1} $
$\clubsuit \,$ Menentukan nilai $ a \, $ dan $ b $
$\begin{align} s_n & = 2n^2 - n \\ a & = u_1 = s_1 = 2.1^2 - 1 = 1 \\ u_2 & = s_2 - s_1 \\ u_2 & = (2.2^2 - 2) - 1 = 6 - 1 = 5 \\ b & = u_2 - u_1 = 5 - 1 = 4 \end{align}$
sehingga nilai $ a = 1 \, $ dan $ b = 4 $
$\clubsuit \,$ Menentukan suku ke-12
$\begin{align} u_n & = a+(n-1)b \\ u_{12} & = 1+(12-1).4 \\ u_{12} & = 1+44 \\ u_{12} & = 45 \end{align}$
sehingga nilai $ u_{12} = 45 $
$\clubsuit \,$ Berdasarkan petunjuk B
Pernyataan pertama : $ u_{12} = 45 \, $ (benar)
Pernyataan kedua : $ a = 1 \, $ dan $ b = 4 \, $ (benar)
Karena kedua pernyataan benar dan saling berhubungan, maka berdasarkan petunjuk B jawabannya A.
Jadi, jawabannya A. $ \heartsuit $
Nomor 10
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Apabila $ a = 0 \, $ dan $ b \, $ sembarang, maka matriks $ \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \, $ tidak mempunyai invers .
SEBAB
Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol.
Apabila $ a = 0 \, $ dan $ b \, $ sembarang, maka matriks $ \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \, $ tidak mempunyai invers .
SEBAB
Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol.
$\spadesuit \, $ Konsep Matriks
*) Determinan
$ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow Det(A) = ad-bc $
*) Suatu matriks tidak mempunyai invers jika nilai determinannya sama dengan nol.
$\spadesuit \, $ Menentukan determinan matriksnya
$\begin{align} A & = \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \\ Det(A) & = a.a - (a-b)(a+b) \\ Det(A) & = a^2 - (a^2-b^2) \\ Det(A) & = b^2 \end{align}$
Karena nilai $ b \, $ sembarang, maka nilai $ Det(A) \, $ tidak selalu sama dengan nol, artinya Det(A) nilainya bisa nol atau tidak nol, sehingga matriks tersebut bisa mempunyai invers atau juga bisa tidak punya invers.
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : Matriks tidak punya invers (salah)
Pernyataan kedua : Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol. (Benar)
Karena pernyataan pertama salah dan pernyataan kedua benar, berdasarkan petunjuk B jawabannya D.
Jadi, jawabannya D. $ \heartsuit $
*) Determinan
$ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow Det(A) = ad-bc $
*) Suatu matriks tidak mempunyai invers jika nilai determinannya sama dengan nol.
$\spadesuit \, $ Menentukan determinan matriksnya
$\begin{align} A & = \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \\ Det(A) & = a.a - (a-b)(a+b) \\ Det(A) & = a^2 - (a^2-b^2) \\ Det(A) & = b^2 \end{align}$
Karena nilai $ b \, $ sembarang, maka nilai $ Det(A) \, $ tidak selalu sama dengan nol, artinya Det(A) nilainya bisa nol atau tidak nol, sehingga matriks tersebut bisa mempunyai invers atau juga bisa tidak punya invers.
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : Matriks tidak punya invers (salah)
Pernyataan kedua : Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol. (Benar)
Karena pernyataan pertama salah dan pernyataan kedua benar, berdasarkan petunjuk B jawabannya D.
Jadi, jawabannya D. $ \heartsuit $