Nomor 1
Jika jumlah kuadrat akar-akar persamaan $ x^2-3x+n=0 \, $ sama dengan jumlah pangkat tiga akar-akar persamaan $ x^2 + x -n =0 , \, $
maka nilai $ n \, $ adalah ....
$\clubsuit \, $ PKI : $ x^2-3x+n=0 \, $ dengan akar-akar $ x_1 $ dan $ x_2 $
$ x_1 + x_2 = \frac{-b}{a} = \frac{-(-3)}{1} = 3 $
$ x_1 . x_2 = \frac{c}{a} = \frac{n}{1} = n $
$\clubsuit \, $ PKII : $ x^2 + x -n =0 \, $ dengan akar-akar $ y_1 $ dan $ y_2 $
$ y_1 + y_2 = \frac{-b}{a} = \frac{-1}{1} = -1 $
$ y_1 . y_2 = \frac{c}{a} = \frac{-n}{1} = -n $
$\clubsuit \, $ Menentukan nilai $ n $ dengan jumlah kuadrat PKI sama dengan jumlah pangkat tiga PKII
$\begin{align} x_1^2 + x_2^2 & = y_1^3 + y_2^3 \\ (x_1+x_2)^2 - 2x_1x_2 & = (y_1+y_2)^2 - 3y_1y_2(y_1+y_2) \\ 3^2 - 2.n & = (-1)^3 - 3. (-n) . (-1) \\ 9 - 2n & = -1 - 3n \\ n & = -10 \end{align}$
Jadi, nilai $ n = -10 . \heartsuit $
$ x_1 + x_2 = \frac{-b}{a} = \frac{-(-3)}{1} = 3 $
$ x_1 . x_2 = \frac{c}{a} = \frac{n}{1} = n $
$\clubsuit \, $ PKII : $ x^2 + x -n =0 \, $ dengan akar-akar $ y_1 $ dan $ y_2 $
$ y_1 + y_2 = \frac{-b}{a} = \frac{-1}{1} = -1 $
$ y_1 . y_2 = \frac{c}{a} = \frac{-n}{1} = -n $
$\clubsuit \, $ Menentukan nilai $ n $ dengan jumlah kuadrat PKI sama dengan jumlah pangkat tiga PKII
$\begin{align} x_1^2 + x_2^2 & = y_1^3 + y_2^3 \\ (x_1+x_2)^2 - 2x_1x_2 & = (y_1+y_2)^2 - 3y_1y_2(y_1+y_2) \\ 3^2 - 2.n & = (-1)^3 - 3. (-n) . (-1) \\ 9 - 2n & = -1 - 3n \\ n & = -10 \end{align}$
Jadi, nilai $ n = -10 . \heartsuit $
Nomor 2
Nilai $ x \, $ yang memenuhi persamaan :
$ {}^2 \log \, {}^2 \log \left( 2^{x+1} + 3 \right) = 1 + {}^2 \log x $
adalah .....
$ {}^2 \log \, {}^2 \log \left( 2^{x+1} + 3 \right) = 1 + {}^2 \log x $
adalah .....
$\spadesuit \, $ Konsep logaritma :
persamaan : $ {}^a \log f(x) = {}^a \log g(x) \rightarrow f(x) = g(x) $
definisi : $a^x = c \rightarrow x = {}^a \log c $
Sifat : $ {}^a \log b ^ n = n. {}^a \log b \, \, \, $ dan $ \, {}^a \log b + {}^a \log c = {}^a \log (bc) $
$\spadesuit \, $ Misalkan $ p = 2^x \, $ dengan nilai $ p $ positif
$\begin{align} {}^2 \log \, {}^2 \log \left( 2^{x+1} + 3 \right) & = 1 + {}^2 \log x \\ {}^2 \log \,\left[ {}^2 \log \left( 2^{x+1} + 3 \right) \right] & = {}^2 \log 2 + {}^2 \log x \\ {}^2 \log \,\left[ {}^2 \log \left( 2^{x+1} + 3 \right) \right] & = {}^2 \log (2x) \\ \text{(coret } \, {}^2 \log \, \text{ paling } \, & \text{ luar ) } \\ {}^2 \log \left( 2^{x+1} + 3 \right) & = 2x \\ {}^2 \log \left( 2^{x+1} + 3 \right) & = {}^2 \log 2^{2x} \, \, \text{(coret } \, {}^2 \log \, ) \\ 2^{x+1} + 3 & = 2^{2x} \\ 2^{2x} - 2^{x+1} - 3 & = 0 \\ (2^x)^2 - 2^1 . 2^x - 3 & = 0 \, \, \text{(subst. } p = 2^x \, ) \\ p^2 - 2p - 3 & = 0 \\ (p+1)(p-3) & = 0 \\ p = -1 \vee p = 3 \end{align}$
yang memenuhi $ p = 3 \, $ karena nilai $ p $ harus positif.
sehingga : $ p = 3 \rightarrow 2^x = 3 \rightarrow x = {}^2 \log 3 $
Jadi, nilai $ x = {}^2 \log 3 . \heartsuit $
persamaan : $ {}^a \log f(x) = {}^a \log g(x) \rightarrow f(x) = g(x) $
definisi : $a^x = c \rightarrow x = {}^a \log c $
Sifat : $ {}^a \log b ^ n = n. {}^a \log b \, \, \, $ dan $ \, {}^a \log b + {}^a \log c = {}^a \log (bc) $
$\spadesuit \, $ Misalkan $ p = 2^x \, $ dengan nilai $ p $ positif
$\begin{align} {}^2 \log \, {}^2 \log \left( 2^{x+1} + 3 \right) & = 1 + {}^2 \log x \\ {}^2 \log \,\left[ {}^2 \log \left( 2^{x+1} + 3 \right) \right] & = {}^2 \log 2 + {}^2 \log x \\ {}^2 \log \,\left[ {}^2 \log \left( 2^{x+1} + 3 \right) \right] & = {}^2 \log (2x) \\ \text{(coret } \, {}^2 \log \, \text{ paling } \, & \text{ luar ) } \\ {}^2 \log \left( 2^{x+1} + 3 \right) & = 2x \\ {}^2 \log \left( 2^{x+1} + 3 \right) & = {}^2 \log 2^{2x} \, \, \text{(coret } \, {}^2 \log \, ) \\ 2^{x+1} + 3 & = 2^{2x} \\ 2^{2x} - 2^{x+1} - 3 & = 0 \\ (2^x)^2 - 2^1 . 2^x - 3 & = 0 \, \, \text{(subst. } p = 2^x \, ) \\ p^2 - 2p - 3 & = 0 \\ (p+1)(p-3) & = 0 \\ p = -1 \vee p = 3 \end{align}$
yang memenuhi $ p = 3 \, $ karena nilai $ p $ harus positif.
sehingga : $ p = 3 \rightarrow 2^x = 3 \rightarrow x = {}^2 \log 3 $
Jadi, nilai $ x = {}^2 \log 3 . \heartsuit $
Nomor 3
Garis singgung pada kurva $ x^2 - y + 2x - 3 = 0 \, $ yang tegak lurus pada garis $ x-2y+3 = 0 \, $ mempunyai persamaan .....
$\clubsuit \, $ Menentukan gradien garis
$ x - 2y + 3 = 0 \rightarrow y = \frac{1}{2}x + \frac{3}{2} \rightarrow m_1 = \frac{1}{2} $
Karena tegak lurus, maka gradien garis singgungnya ($m$) :
$ m.m_1 = -1 \rightarrow m = \frac{-1}{m_1} = \frac{-1}{\frac{1}{2}} = -2 $
sehingga gradien garis sinngungnya $ m = -2 $
$\clubsuit \, $ Gradien garis singgung : $ m = y^\prime $
$\begin{align} x^2 - y + 2x - 3 = 0 \rightarrow y & = x^2+2x - 3 \\ y^\prime & = 2x + 2 \\ m & = y^\prime \\ -2 & = 2x + 2 \\ x & = -2 \end{align}$
$\clubsuit \, $ Menentukan titik singgung dengan substitusi $ x = -2 $
$\begin{align} x = -2 \rightarrow y & = x^2+2x - 3 \\ y & = (-2)^2+2.(-2) - 3 \\ y & = -3 \end{align}$
Sehingga titik singgungnya (-2,-3)
$\clubsuit \, $ Menentukan persamaan garis singgung di titik ($x_1,y_1$) = (-2,-3) dengan gradien $ m = -2 $
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-3) & = -2(x-(-2)) \\ y+3 & = -2 ( x+2) \\ y+3 & = -2x - 4 \\ y+2x+7 & = 0 \end{align}$
Jadi, PGS nya adalah $ y+2x+7 = 0 . \heartsuit$
$ x - 2y + 3 = 0 \rightarrow y = \frac{1}{2}x + \frac{3}{2} \rightarrow m_1 = \frac{1}{2} $
Karena tegak lurus, maka gradien garis singgungnya ($m$) :
$ m.m_1 = -1 \rightarrow m = \frac{-1}{m_1} = \frac{-1}{\frac{1}{2}} = -2 $
sehingga gradien garis sinngungnya $ m = -2 $
$\clubsuit \, $ Gradien garis singgung : $ m = y^\prime $
$\begin{align} x^2 - y + 2x - 3 = 0 \rightarrow y & = x^2+2x - 3 \\ y^\prime & = 2x + 2 \\ m & = y^\prime \\ -2 & = 2x + 2 \\ x & = -2 \end{align}$
$\clubsuit \, $ Menentukan titik singgung dengan substitusi $ x = -2 $
$\begin{align} x = -2 \rightarrow y & = x^2+2x - 3 \\ y & = (-2)^2+2.(-2) - 3 \\ y & = -3 \end{align}$
Sehingga titik singgungnya (-2,-3)
$\clubsuit \, $ Menentukan persamaan garis singgung di titik ($x_1,y_1$) = (-2,-3) dengan gradien $ m = -2 $
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-3) & = -2(x-(-2)) \\ y+3 & = -2 ( x+2) \\ y+3 & = -2x - 4 \\ y+2x+7 & = 0 \end{align}$
Jadi, PGS nya adalah $ y+2x+7 = 0 . \heartsuit$
Nomor 4
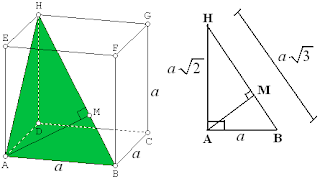
Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Perbandingan
antara volume limas P.BCS dan volume kubus ABCD.EFGH adalah .....
$\spadesuit \, $ Gambar

Misalkan rusuk kubus adalah $ a \, $ cm. Tinggi limas P.BCS adalah $ \frac{1}{2}a $
$L_{\Delta BCS} = \frac{1}{2}.BC.CS = \frac{1}{2}.a.\frac{1}{2}a $
$\spadesuit \, $ Menentukan perbandingan volume
$\begin{align} \frac{V_{P.BCS}}{V_{kubus}} & = \frac{\frac{1}{3} L_{\Delta BCS} . t}{s^3} \\ & = \frac{\frac{1}{3} .(\frac{1}{2}.a.\frac{1}{2}a) . \frac{1}{2}a }{a.a.a} \\ & = \frac{1}{24} \end{align}$
Jadi, perbandingannya adalah 1 : 24 . $ \heartsuit $

Misalkan rusuk kubus adalah $ a \, $ cm. Tinggi limas P.BCS adalah $ \frac{1}{2}a $
$L_{\Delta BCS} = \frac{1}{2}.BC.CS = \frac{1}{2}.a.\frac{1}{2}a $
$\spadesuit \, $ Menentukan perbandingan volume
$\begin{align} \frac{V_{P.BCS}}{V_{kubus}} & = \frac{\frac{1}{3} L_{\Delta BCS} . t}{s^3} \\ & = \frac{\frac{1}{3} .(\frac{1}{2}.a.\frac{1}{2}a) . \frac{1}{2}a }{a.a.a} \\ & = \frac{1}{24} \end{align}$
Jadi, perbandingannya adalah 1 : 24 . $ \heartsuit $
Nomor 5
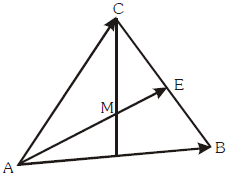
Pada segitiga ABC, E adalah titik tengah BC dan M adalah titik berat segitiga tersebut.
Jika $ \vec{u} = \vec{AB} \, $ dan $ \vec{v} = \vec{AC}, \, $ maka ruas garis berarah $ \vec{ME} \, $ dapat dinyatakan dalam $ \vec{u} \, $ dan $ \vec{v} \, $ sebagai .....

Pada segitiga ABC, E adalah titik tengah BC dan M adalah titik berat segitiga tersebut.
Jika $ \vec{u} = \vec{AB} \, $ dan $ \vec{v} = \vec{AC}, \, $ maka ruas garis berarah $ \vec{ME} \, $ dapat dinyatakan dalam $ \vec{u} \, $ dan $ \vec{v} \, $ sebagai .....
$\clubsuit \, $ Konsep dasar vektor
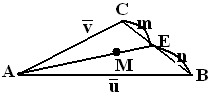
$ \vec{AE} = \frac{m\vec{u} + n\vec{v}}{m+n} $
AE garis berat sehingga titik E ditengah BC.
Jika M titik berat, maka $ \vec{ME} = \frac{1}{3}\vec{AE} $
$\clubsuit \, $ Menentukan vektor $ \vec{AE} \, $ dan $ \vec{ME} $
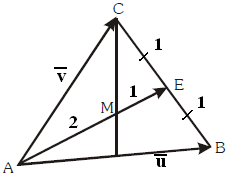
$\begin{align} \vec{AE} & = \frac{m\vec{u} + n\vec{v}}{m+n} = \frac{1.\vec{u} + 1.\vec{v}}{1+1} = \frac{\vec{u} + \vec{v}}{2} \\ \vec{ME} & = \frac{1}{3}\vec{AE} \\ & = \frac{1}{3}. \frac{\vec{u} + \vec{v}}{2} \\ \vec{ME} & = \frac{1}{6}\vec{u} + \frac{1}{6}\vec{v} \end{align}$
Jadi, vektor $ \vec{ME} = \frac{1}{6}\vec{u} + \frac{1}{6}\vec{v} . \heartsuit$

$ \vec{AE} = \frac{m\vec{u} + n\vec{v}}{m+n} $
AE garis berat sehingga titik E ditengah BC.
Jika M titik berat, maka $ \vec{ME} = \frac{1}{3}\vec{AE} $
$\clubsuit \, $ Menentukan vektor $ \vec{AE} \, $ dan $ \vec{ME} $

$\begin{align} \vec{AE} & = \frac{m\vec{u} + n\vec{v}}{m+n} = \frac{1.\vec{u} + 1.\vec{v}}{1+1} = \frac{\vec{u} + \vec{v}}{2} \\ \vec{ME} & = \frac{1}{3}\vec{AE} \\ & = \frac{1}{3}. \frac{\vec{u} + \vec{v}}{2} \\ \vec{ME} & = \frac{1}{6}\vec{u} + \frac{1}{6}\vec{v} \end{align}$
Jadi, vektor $ \vec{ME} = \frac{1}{6}\vec{u} + \frac{1}{6}\vec{v} . \heartsuit$