Nomor 1
Jika $ x $ dan $ y $ memenuhi pertaksamaan $ y^2 - 2 < x $ dan persamaan $ 2y - x + 1 = 0 $ , maka
$ x+y $ memenuhi pertaksamaan ....
$\clubsuit \, $ Substitusi pers(i) ke perts(ii)
$ 2y - x + 1 = 0 \rightarrow x = 2y + 1 \, $ ....pers(i)
$ y^2 - 2 < x \rightarrow y^2 - 2 - x < 0 $
$\begin{align} \text{perts(ii) : } \, y^2 - 2 - x & < 0 \\ y^2 - 2 - (2y + 1) & < 0 \\ y^2 - 2y - 3 & < 0 \\ (y+1)(y-3) & < 0 \\ y = -1 \vee y & = 3 \end{align}$

sehingga nilai $ y $ : $ \, -1 < y < 3 $
$\clubsuit \, $ Substitusi nilai $ y $ ke pers(i)
$ y = 3 \rightarrow x = 2y + 1 = 2.3+1 = 7 $
$ y = -1 \rightarrow x = 2y + 1 = 2.(-1)+1 = -1 $
sehingga nilai $ x $ : $ \, -1 < x < 7 $
Jumlah nilai $ x $ dan $ y \, $ , diperoleh :
$ \begin{array}{cc} -1 < y < 3 & \\ -1 < x < 7 & + \\ \hline -2 < x + y < 10 & \end{array} $
Jadi, diperoleh $ -2 < x + y < 10 . \heartsuit $
$ 2y - x + 1 = 0 \rightarrow x = 2y + 1 \, $ ....pers(i)
$ y^2 - 2 < x \rightarrow y^2 - 2 - x < 0 $
$\begin{align} \text{perts(ii) : } \, y^2 - 2 - x & < 0 \\ y^2 - 2 - (2y + 1) & < 0 \\ y^2 - 2y - 3 & < 0 \\ (y+1)(y-3) & < 0 \\ y = -1 \vee y & = 3 \end{align}$

sehingga nilai $ y $ : $ \, -1 < y < 3 $
$\clubsuit \, $ Substitusi nilai $ y $ ke pers(i)
$ y = 3 \rightarrow x = 2y + 1 = 2.3+1 = 7 $
$ y = -1 \rightarrow x = 2y + 1 = 2.(-1)+1 = -1 $
sehingga nilai $ x $ : $ \, -1 < x < 7 $
Jumlah nilai $ x $ dan $ y \, $ , diperoleh :
$ \begin{array}{cc} -1 < y < 3 & \\ -1 < x < 7 & + \\ \hline -2 < x + y < 10 & \end{array} $
Jadi, diperoleh $ -2 < x + y < 10 . \heartsuit $
Nomor 2
Jika salah satu akar persamaan $ \frac{x}{6} - \frac{k}{x} = \frac{1}{2} \, $ adalah -6, maka akar yang lain adalah ....
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{x}{6} - \frac{k}{x} & = \frac{1}{2} \, \, \text{ ( kali } 6x ) \\ x^2 - 6k & = 3x \\ x^2 - 3x - 6k & = 0 \\ a = 1, \, b = -3, \, c & = -6k \end{align}$
$\spadesuit \, $ Salah satu akarnya -6 , artinya $ x_1 = -6 $
$\spadesuit \, $ Menentukan nilai $ k $ dengan substitusi $ x_1 = -6 $
$\begin{align} x_1 = -6 \rightarrow x^2 - 3x - 6k & = 0 \\ (-6)^2 - 3.(-6) - 6k & = 0 \\ 36 + 18 - 6k & = 0 \\ k & = 9 \end{align}$
PK : $ x^2 - 3x - 6.9 = 0 \rightarrow x^2 - 3x - 54 = 0 $
$\spadesuit \, $ Menentukan akar-akar dengan pemfaktoran
$\begin{align} x^2 - 3x - 54 & = 0 \\ (x + 6)(x-9) & = 0 \\ x= -6 \vee x & = 9 \end{align}$
Jadi, akar yang lainnya adalah 9. $ \heartsuit $
$\begin{align} \frac{x}{6} - \frac{k}{x} & = \frac{1}{2} \, \, \text{ ( kali } 6x ) \\ x^2 - 6k & = 3x \\ x^2 - 3x - 6k & = 0 \\ a = 1, \, b = -3, \, c & = -6k \end{align}$
$\spadesuit \, $ Salah satu akarnya -6 , artinya $ x_1 = -6 $
$\spadesuit \, $ Menentukan nilai $ k $ dengan substitusi $ x_1 = -6 $
$\begin{align} x_1 = -6 \rightarrow x^2 - 3x - 6k & = 0 \\ (-6)^2 - 3.(-6) - 6k & = 0 \\ 36 + 18 - 6k & = 0 \\ k & = 9 \end{align}$
PK : $ x^2 - 3x - 6.9 = 0 \rightarrow x^2 - 3x - 54 = 0 $
$\spadesuit \, $ Menentukan akar-akar dengan pemfaktoran
$\begin{align} x^2 - 3x - 54 & = 0 \\ (x + 6)(x-9) & = 0 \\ x= -6 \vee x & = 9 \end{align}$
Jadi, akar yang lainnya adalah 9. $ \heartsuit $
Cara II
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{x}{6} - \frac{k}{x} & = \frac{1}{2} \, \, \text{ ( kali } 6x ) \\ x^2 - 6k & = 3x \\ x^2 - 3x - 6k & = 0 \\ a = 1, \, b = -3, \, c & = -6k \end{align}$
$\spadesuit \, $ Salah satu akarnya -6 , artinya $ x_1 = -6 $
$\spadesuit \, $ Menentukan $ x_2 $ dari operasi akar
$\begin{align} x_1 + x_2 & = \frac{-b}{a} \\ -6 + x_2 & = \frac{-(-3)}{1} \\ -6 + x_2 & = 3 \\ x_2 & = 9 \end{align}$
Jadi, akar yang lainnya adalah 9. $ \heartsuit $
Catatan : Pada pembahasan ini tidak perlu menentukan nilai $ k $ dulu
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} \frac{x}{6} - \frac{k}{x} & = \frac{1}{2} \, \, \text{ ( kali } 6x ) \\ x^2 - 6k & = 3x \\ x^2 - 3x - 6k & = 0 \\ a = 1, \, b = -3, \, c & = -6k \end{align}$
$\spadesuit \, $ Salah satu akarnya -6 , artinya $ x_1 = -6 $
$\spadesuit \, $ Menentukan $ x_2 $ dari operasi akar
$\begin{align} x_1 + x_2 & = \frac{-b}{a} \\ -6 + x_2 & = \frac{-(-3)}{1} \\ -6 + x_2 & = 3 \\ x_2 & = 9 \end{align}$
Jadi, akar yang lainnya adalah 9. $ \heartsuit $
Catatan : Pada pembahasan ini tidak perlu menentukan nilai $ k $ dulu
Nomor 3
$ \int \limits_{-3}^{3} | x^2 - 2x - 3 | \, dx = .... $
$\clubsuit \, $ Menentukan interval positif dan negatif fungsi
$\begin{align} x^2 - 2x - 3 & = 0 \\ (x+1)(x-3) & = 0 \\ x = -1 \vee x & = 3 \end{align}$
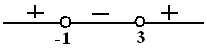
Artinya fungsi $ f(x) = x^2 - 2x - 3 \, $ bernilai negatif saat $ -1 \leq x \leq 3 \, $ dan selain itu positif.
$\clubsuit \, $ Definisi harga mutlak
$|f(x)| = \left\{ \begin{array}{cc} f(x) & , \text{untuk } f(x) \geq 0 \, \text{(positif)} \\ -f(x) & , \text{untuk } f(x) < 0 \, \text{(negatif)} \\ \end{array} \right. $
Sehingga untuk $ f(x) = x^2 - 2x - 3 \, $
$|x^2 - 2x - 3| = \left\{ \begin{array}{cc} x^2 - 2x - 3 & , x \leq -1 \vee x \geq 3 \\ -(x^2 - 2x - 3) & , -1 < x < 3 \\ \end{array} \right. $
Artinya :
Untuk $ x \leq -1 \vee x \geq 3 \rightarrow |x^2 - 2x - 3| = x^2 - 2x - 3 $
Untuk $ -1 < x < 3 $
$ \rightarrow |x^2 - 2x - 3| = -(x^2 - 2x - 3) = -x^2 + 2x + 3 $
$\clubsuit \, $ Sifat integral : $ \int \limits_{a}^{c} f(x) dx = \int \limits_{a}^{b} f(x) dx + \int \limits_{b}^{c} f(x) dx $
$\clubsuit \, $ Menyelesaikan integral dengan sifat dan harga mutlak
$\begin{align} & \int \limits_{-3}^{3} | x^2 - 2x - 3 | \, dx \\ & = \int \limits_{-3}^{-1} | x^2 - 2x - 3 | \, dx + \int \limits_{-1}^{3} | x^2 - 2x - 3 | \, dx \\ & = \int \limits_{-3}^{-1} (x^2 - 2x - 3) \, dx + \int \limits_{-1}^{3} (-x^2 + 2x + 3) \, dx \\ & = \left( \frac{1}{3} x^3 - x^2 - 3x \right)_{-3}^{-1} + \left( -\frac{1}{3} x^3 + x^2 + 3x \right)_{-1}^{3} \\ & = \frac{32}{3} + \frac{32}{3} = \frac{64}{3} \end{align}$
Jadi, hasil integralnya adalah $ \frac{64}{3} . \heartsuit$
Catatan : Soal ini sulit karena melibatkan harga mutlak dan batasnya harus dipecah.
$\begin{align} x^2 - 2x - 3 & = 0 \\ (x+1)(x-3) & = 0 \\ x = -1 \vee x & = 3 \end{align}$
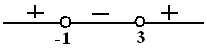
Artinya fungsi $ f(x) = x^2 - 2x - 3 \, $ bernilai negatif saat $ -1 \leq x \leq 3 \, $ dan selain itu positif.
$\clubsuit \, $ Definisi harga mutlak
$|f(x)| = \left\{ \begin{array}{cc} f(x) & , \text{untuk } f(x) \geq 0 \, \text{(positif)} \\ -f(x) & , \text{untuk } f(x) < 0 \, \text{(negatif)} \\ \end{array} \right. $
Sehingga untuk $ f(x) = x^2 - 2x - 3 \, $
$|x^2 - 2x - 3| = \left\{ \begin{array}{cc} x^2 - 2x - 3 & , x \leq -1 \vee x \geq 3 \\ -(x^2 - 2x - 3) & , -1 < x < 3 \\ \end{array} \right. $
Artinya :
Untuk $ x \leq -1 \vee x \geq 3 \rightarrow |x^2 - 2x - 3| = x^2 - 2x - 3 $
Untuk $ -1 < x < 3 $
$ \rightarrow |x^2 - 2x - 3| = -(x^2 - 2x - 3) = -x^2 + 2x + 3 $
$\clubsuit \, $ Sifat integral : $ \int \limits_{a}^{c} f(x) dx = \int \limits_{a}^{b} f(x) dx + \int \limits_{b}^{c} f(x) dx $
$\clubsuit \, $ Menyelesaikan integral dengan sifat dan harga mutlak
$\begin{align} & \int \limits_{-3}^{3} | x^2 - 2x - 3 | \, dx \\ & = \int \limits_{-3}^{-1} | x^2 - 2x - 3 | \, dx + \int \limits_{-1}^{3} | x^2 - 2x - 3 | \, dx \\ & = \int \limits_{-3}^{-1} (x^2 - 2x - 3) \, dx + \int \limits_{-1}^{3} (-x^2 + 2x + 3) \, dx \\ & = \left( \frac{1}{3} x^3 - x^2 - 3x \right)_{-3}^{-1} + \left( -\frac{1}{3} x^3 + x^2 + 3x \right)_{-1}^{3} \\ & = \frac{32}{3} + \frac{32}{3} = \frac{64}{3} \end{align}$
Jadi, hasil integralnya adalah $ \frac{64}{3} . \heartsuit$
Catatan : Soal ini sulit karena melibatkan harga mutlak dan batasnya harus dipecah.
Nomor 4
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ a $ . P dan Q masing - masing merupakan titik tengah AB dan CD,
sedangkan R merupakan titik perpotongan EG dan FH. Jarak titik R ke bidang EPQH adalah ....
$\spadesuit \, $ Gambar

Jarak R ke bidang EPQH = panjang RO ( jarak terdekatnya)
$ NR = \frac{1}{2} NK = \frac{1}{2} a $
$ MN = \sqrt{MR^2 + RN^2 } = \sqrt{a^2 + (\frac{1}{2} a)^2 } = \frac{1}{2}a\sqrt{5} $
$\spadesuit \, $ Menentukan panjang RO dengan luas segitiga MNR
$\begin{align} L_{\Delta MNR} \text{(alas MR)} & = L_{\Delta MNR} \text{(alas MN)} \\ \frac{1}{2} . MR. RN & = \frac{1}{2} . MN . RO \\ MR. RN & = MN . RO \\ a. \frac{1}{2} a & = \frac{1}{2} a \sqrt{5} . RO \\ a & = \sqrt{5} . RO \\ RO & = \frac{a}{\sqrt{5}} = \frac{a}{5} \sqrt{5} \end{align}$
Jadi, jaraknya adalah $ \frac{a}{5} \sqrt{5} . \heartsuit $

Jarak R ke bidang EPQH = panjang RO ( jarak terdekatnya)
$ NR = \frac{1}{2} NK = \frac{1}{2} a $
$ MN = \sqrt{MR^2 + RN^2 } = \sqrt{a^2 + (\frac{1}{2} a)^2 } = \frac{1}{2}a\sqrt{5} $
$\spadesuit \, $ Menentukan panjang RO dengan luas segitiga MNR
$\begin{align} L_{\Delta MNR} \text{(alas MR)} & = L_{\Delta MNR} \text{(alas MN)} \\ \frac{1}{2} . MR. RN & = \frac{1}{2} . MN . RO \\ MR. RN & = MN . RO \\ a. \frac{1}{2} a & = \frac{1}{2} a \sqrt{5} . RO \\ a & = \sqrt{5} . RO \\ RO & = \frac{a}{\sqrt{5}} = \frac{a}{5} \sqrt{5} \end{align}$
Jadi, jaraknya adalah $ \frac{a}{5} \sqrt{5} . \heartsuit $
Nomor 5
Diketahui suatu persamaan parabola $ y = ax^2 + bx + c. \, $ Jika $ a, \, b \, $ dan $ c \, $ berturut - turut merupakan
suku pertama, kedua, dan ketiga suatu barisan aritmetika, serta garis singgung parabola tersebut di titik (1,12) sejajar
dengan garis $ y = 6x $ , maka nilai $ (3a + 2b + c ) = .... $
$\clubsuit \, $ Barisan aritmatika : $ a, \, b, \, c $
Selisih sama : $ b - a = c - b \rightarrow a + c = 2b \, $ ....pers(i)
$\clubsuit \, $ Substitusi titik (1,12) ke parabola
$\begin{align} (1,12) \rightarrow y & = ax^2 + bx + c \\ 12 & = a.1^2 + b.1 + c \\ a + b + c & = 12 \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$\begin{align} a + b + c & = 12 \\ (a+c) + b & = 12 \\ 2b + b & = 12 \rightarrow b = 4 \end{align}$
$\clubsuit \, $ Gradien garis : $ y = 6x \rightarrow m_1 = 6 $
Karena sejajar, maka gradien garis singgungnya sama dengan gradien garis $ y = 6x $ , sehingga $ m = 6 $
$\clubsuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$\begin{align} y & = ax^2 + bx + c \rightarrow y^\prime = 2ax + b \\ m & = f^\prime (1) \\ 6 & = 2a.1 + b \\ 2a + b & = 6 \\ b = 4 \rightarrow 2a + 4 & = 6 \\ 2a & = 2 \rightarrow a = 1 \end{align}$
pers(i) : $ a + c = 2b \rightarrow 1 + c = 2.4 \rightarrow c = 7 $
Sehingga nilai $ 3a + 2b + c = 3.1 + 2.4 + 7 = 3 + 8 + 7 = 18 $
Jadi, nilai $ 3a + 2b + c = 18 . \heartsuit$
Selisih sama : $ b - a = c - b \rightarrow a + c = 2b \, $ ....pers(i)
$\clubsuit \, $ Substitusi titik (1,12) ke parabola
$\begin{align} (1,12) \rightarrow y & = ax^2 + bx + c \\ 12 & = a.1^2 + b.1 + c \\ a + b + c & = 12 \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$\begin{align} a + b + c & = 12 \\ (a+c) + b & = 12 \\ 2b + b & = 12 \rightarrow b = 4 \end{align}$
$\clubsuit \, $ Gradien garis : $ y = 6x \rightarrow m_1 = 6 $
Karena sejajar, maka gradien garis singgungnya sama dengan gradien garis $ y = 6x $ , sehingga $ m = 6 $
$\clubsuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$\begin{align} y & = ax^2 + bx + c \rightarrow y^\prime = 2ax + b \\ m & = f^\prime (1) \\ 6 & = 2a.1 + b \\ 2a + b & = 6 \\ b = 4 \rightarrow 2a + 4 & = 6 \\ 2a & = 2 \rightarrow a = 1 \end{align}$
pers(i) : $ a + c = 2b \rightarrow 1 + c = 2.4 \rightarrow c = 7 $
Sehingga nilai $ 3a + 2b + c = 3.1 + 2.4 + 7 = 3 + 8 + 7 = 18 $
Jadi, nilai $ 3a + 2b + c = 18 . \heartsuit$
