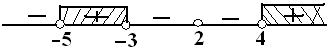Nomor 21
Jika $f(x)=\sqrt{x+1} $ dan $g(x)=\frac{1}{x^2-1} $ , maka daerah asal fungsi komposisi $(g \circ f)(x) $ adalah ....
$\spadesuit \, $ Konsep dasar
Daerah asal $g \circ f $ adalah $\{ D_f \cap D_{g\circ f} \} $
$\spadesuit \, $ Menentukan daerah asal $f(x) $ yaitu $D_f$
$f(x)=\sqrt{x+1} \rightarrow D_f = \{ x+1 \geq 0 \} = \{ x \geq -1 \} $
$\spadesuit \, $ Menentukan daerah asal $D_{g\circ f} $
$g\circ f = g(f(x)) = \frac{1}{(\sqrt{x+1})^2 -1} = \frac{1}{x} $
$D_{g\circ f} = \{ x \neq 0 \} $
$\spadesuit \, $ Menentukan daerah asal $g\circ f $
$\{ D_f \cap D_{g\circ f} \} = \{x\geq -1\} \cap \{x \neq 0 \} = \{-1\leq x < 0 \vee x > 0 \} $
Jadi, daerah asal $g\circ f $ adalah $ \{-1\leq x < 0 \vee x > 0 \} . \heartsuit $
Daerah asal $g \circ f $ adalah $\{ D_f \cap D_{g\circ f} \} $
$\spadesuit \, $ Menentukan daerah asal $f(x) $ yaitu $D_f$
$f(x)=\sqrt{x+1} \rightarrow D_f = \{ x+1 \geq 0 \} = \{ x \geq -1 \} $
$\spadesuit \, $ Menentukan daerah asal $D_{g\circ f} $
$g\circ f = g(f(x)) = \frac{1}{(\sqrt{x+1})^2 -1} = \frac{1}{x} $
$D_{g\circ f} = \{ x \neq 0 \} $
$\spadesuit \, $ Menentukan daerah asal $g\circ f $
$\{ D_f \cap D_{g\circ f} \} = \{x\geq -1\} \cap \{x \neq 0 \} = \{-1\leq x < 0 \vee x > 0 \} $
Jadi, daerah asal $g\circ f $ adalah $ \{-1\leq x < 0 \vee x > 0 \} . \heartsuit $
Nomor 22
Pada matriks $A = \left( \begin{matrix} 1 & a \\ b & c \end{matrix} \right) $ , jika bilangan positif $1,a,c $ membentuk barisan geometri
berjumlah 13 dan bilangan $1,b,c $ membentuk barisan aritmetika, maka det A = ....
$\clubsuit \, $ Barisan geometri : $1,a,c$
Rasio sama : $\frac{a}{1} = \frac{c}{a} \rightarrow c = a^2 $ ...pers(i)
jumlahnya : $1+a+c=13 \rightarrow a+c = 12 $ ...pers(ii)
$\clubsuit \, $ Barisan aritmatika : $1,b,c$
Selisih sama : $ b-1 = c-b \rightarrow 2b = 1 + c $ ...pers(iii)
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$a+c = 12 \rightarrow a + a^2 = 12 \rightarrow a^2+a-12=0 $
$(a-3)(a+4)=0 \rightarrow a=3 \vee a =-4 $
yang memenuhi $a=3 $ (yang positif)
$c = a^2 = 3^2 = 9 $
pers(iii) : $2b = 1+c \rightarrow 2b = 1 + 9 \rightarrow b= 5 $
Matriks $A = \left( \begin{matrix} 1 & a \\ b & c \end{matrix} \right) = \left( \begin{matrix} 1 & 3 \\ 5 & 9 \end{matrix} \right) $
Determinan $A $ : $|A| = 1.9 -5.3 = 9 - 15 = -6 $
Jadi, determinan A adalah $ -6 . \heartsuit $
Rasio sama : $\frac{a}{1} = \frac{c}{a} \rightarrow c = a^2 $ ...pers(i)
jumlahnya : $1+a+c=13 \rightarrow a+c = 12 $ ...pers(ii)
$\clubsuit \, $ Barisan aritmatika : $1,b,c$
Selisih sama : $ b-1 = c-b \rightarrow 2b = 1 + c $ ...pers(iii)
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$a+c = 12 \rightarrow a + a^2 = 12 \rightarrow a^2+a-12=0 $
$(a-3)(a+4)=0 \rightarrow a=3 \vee a =-4 $
yang memenuhi $a=3 $ (yang positif)
$c = a^2 = 3^2 = 9 $
pers(iii) : $2b = 1+c \rightarrow 2b = 1 + 9 \rightarrow b= 5 $
Matriks $A = \left( \begin{matrix} 1 & a \\ b & c \end{matrix} \right) = \left( \begin{matrix} 1 & 3 \\ 5 & 9 \end{matrix} \right) $
Determinan $A $ : $|A| = 1.9 -5.3 = 9 - 15 = -6 $
Jadi, determinan A adalah $ -6 . \heartsuit $
Nomor 23
Jika $U_1,U_2,...,U_7 $ membentuk barisan geometri, $U_3=12 $ dan $\log U_1 + \log U_2 + ... + \log U_7 = 7\log 3 $ , maka $U_5=...$
$\spadesuit \, $ Barisan geometri : $U_n = ar^{n-1} $
$\spadesuit \, $ Menyederhanakan bentuk logaritma
$\begin{align} \log U_1 + \log U_2 + ... + \log U_7 & = 7\log 3 \\ \log (U_1.U_2...U_7) & = \log 3^7 \\ U_1.U_2...U_7 & = 3^7 \\ a.(ar).(ar^2)...(ar^6) & = 3^7 \\ a^7r^{21} & = 3^7 \\ (ar^3)^7 & = 3^7 \\ ar^3 & = 3 \, \, \, \text{...pers(i)} \end{align}$
Suku ketiga : $U_3=12 \rightarrow ar^2 = 12 $ ...pers(ii)
$\spadesuit \, $ Bagi pers(i) dan pers(ii)
$\frac{ar^3}{ar^2} = \frac{3}{12} \rightarrow r = \frac{1}{4} $
pers(ii) : $ar^2 = 12 \rightarrow a\left( \frac{1}{4} \right)^2 = 12 \rightarrow a = 12 \times 4^2 $
$\spadesuit \, $ Menentukan suku kelima
$U_5 = ar^4 = 12 \times 4^2 . \left( \frac{1}{4} \right)^4 = \frac{3}{4} $
Jadi, nilai $ U_5 = \frac{3}{4} .\heartsuit $
$\spadesuit \, $ Menyederhanakan bentuk logaritma
$\begin{align} \log U_1 + \log U_2 + ... + \log U_7 & = 7\log 3 \\ \log (U_1.U_2...U_7) & = \log 3^7 \\ U_1.U_2...U_7 & = 3^7 \\ a.(ar).(ar^2)...(ar^6) & = 3^7 \\ a^7r^{21} & = 3^7 \\ (ar^3)^7 & = 3^7 \\ ar^3 & = 3 \, \, \, \text{...pers(i)} \end{align}$
Suku ketiga : $U_3=12 \rightarrow ar^2 = 12 $ ...pers(ii)
$\spadesuit \, $ Bagi pers(i) dan pers(ii)
$\frac{ar^3}{ar^2} = \frac{3}{12} \rightarrow r = \frac{1}{4} $
pers(ii) : $ar^2 = 12 \rightarrow a\left( \frac{1}{4} \right)^2 = 12 \rightarrow a = 12 \times 4^2 $
$\spadesuit \, $ Menentukan suku kelima
$U_5 = ar^4 = 12 \times 4^2 . \left( \frac{1}{4} \right)^4 = \frac{3}{4} $
Jadi, nilai $ U_5 = \frac{3}{4} .\heartsuit $
Nomor 24
Suatu proyek dapat dikerjakan selama $p$ hari, dengan biaya setiap harinya $(4p+\frac{1500}{p}-40) $ juta rupiah.
Jika biaya minimum proyek tersebut adalah R juta rupiah, maka R = ....
$\clubsuit \,$ Biaya total
$B = p(4p+\frac{1500}{p}-40) = 4p^2 -40p +1500 $
$B^\prime = 8p-40 $ (turunannya)
$\clubsuit \, $ Biaya minimum : Turunannya = 0
$B^\prime = 0 \rightarrow 8p-40 = 0 \rightarrow p=5 $
$\clubsuit \, $ Biaya minimum (R) saat $p=5 $
$\begin{align} R & = 4p^2 -40p +1500 \\ & = 4.5^2 -40.5 +1500 \\ & = 100 - 200 + 1500 \\ R & = 1400 \end{align}$
Jadi, nilai R = 1400. $\heartsuit $
$B = p(4p+\frac{1500}{p}-40) = 4p^2 -40p +1500 $
$B^\prime = 8p-40 $ (turunannya)
$\clubsuit \, $ Biaya minimum : Turunannya = 0
$B^\prime = 0 \rightarrow 8p-40 = 0 \rightarrow p=5 $
$\clubsuit \, $ Biaya minimum (R) saat $p=5 $
$\begin{align} R & = 4p^2 -40p +1500 \\ & = 4.5^2 -40.5 +1500 \\ & = 100 - 200 + 1500 \\ R & = 1400 \end{align}$
Jadi, nilai R = 1400. $\heartsuit $
Nomor 25
Jika $f(x)=\frac{2x+1}{x^2-3} $ , maka turunan pertama dari fungsi $f $ di $-3 $ adalah $f^\prime (-3) = .... $
$\spadesuit \, $ Konsep dasar : $y=\frac{u}{v} \rightarrow y^\prime = \frac{u^\prime .v - u.v^\prime }{v^2} $
$\clubsuit \, $ Menentukan turunannya
$f(x)=\frac{2x+1}{x^2-3} $
$u=2x+1 \rightarrow u^\prime = 2 $
$v=x^2-3 \rightarrow v^\prime = 2x $
$f^\prime (x) = \frac{u^\prime .v - u.v^\prime }{v^2} = \frac{2 .(x^2-3) - (2x+1).2x }{(x^2-3)^2} $
$\clubsuit \, $ Substitusi $x=-3 $ ke turunannya
$f^\prime (-3) = \frac{2 .((-3)^2-3) - (2.(-3)+1).2(-3) }{((-3)^2-3)^2} = \frac{12-30}{36} = \frac{-1}{2} $
Jadi, nilai $ f^\prime (-3) = \frac{-1}{2} . \heartsuit $
$\clubsuit \, $ Menentukan turunannya
$f(x)=\frac{2x+1}{x^2-3} $
$u=2x+1 \rightarrow u^\prime = 2 $
$v=x^2-3 \rightarrow v^\prime = 2x $
$f^\prime (x) = \frac{u^\prime .v - u.v^\prime }{v^2} = \frac{2 .(x^2-3) - (2x+1).2x }{(x^2-3)^2} $
$\clubsuit \, $ Substitusi $x=-3 $ ke turunannya
$f^\prime (-3) = \frac{2 .((-3)^2-3) - (2.(-3)+1).2(-3) }{((-3)^2-3)^2} = \frac{12-30}{36} = \frac{-1}{2} $
Jadi, nilai $ f^\prime (-3) = \frac{-1}{2} . \heartsuit $