Nomor 1
Jika salah satu akar dari persamaan kuadrat $x^2-4(k+1)x+k^2-k+7=0$ bernilai tiga kali dari akar yang lain dan semua akar-akar bernilai
lebih dari 2, maka himpunan semua bilangan $k$ yang memenuhi adalah ...
$\clubsuit \, $ PK $ x^2-4(k+1)x+k^2-k+7=0 \, \, \, \, \, $ akar - akarnya $ x_1 \, $ dan $ x_2 $
$x_1+x_2 = \frac{-b}{a} = \frac{-[-4(k+1)]}{1} = 4(k+1) $
artinya $ x_1 + x_2 = 4(k+1) \, $ ...pers(i)
$\clubsuit \, $ Salah satu akarnya bernilai tiga kali akar yang lainnya
$ x_1 = 3x_2 \, $ ....pers(ii)
$\clubsuit \, $ Substitusi $ x_1 = 3x_2 \, $ ke pers(i)
$ x_1 + x_2 = 4(k+1) \rightarrow 3x_2 + x_2 = 4(k+1) \rightarrow x_2 = k+1 $
$\clubsuit \, $ Substitusi $ x_2 = k+1 \, $ ke PK
$\begin{align} x^2-4(k+1)x+k^2-k+7 & =0 \\ (k+1)^2-4(k+1)(k+1)+k^2-k+7 & =0 \\ 2k^2 + 7k - 4 & = 0 \\ (2k-1)(k+4) & = 0 \\ k = \frac{1}{2} \vee k & = -4 \end{align}$
$\clubsuit \, $ Semua akar-akarnya lebih dari 2
$\begin{align} x_1 > 2 \text{ dan } x_2 & > 2 \\ \text{Jumlahkan keduanya } & \\ x_1 + x_2 & > 2 + 2 \\ x_1 + x_2 & > 4 \\ 4(k+1) & > 4 \\ k+1 & > 1 \\ k & > 0 \end{align}$
Karena nilai $ k > 0 \, $ , maka yang memenuhi adalah $ k = \frac{1}{2} $
Jadi, nilai $ k \, $ yang memenuhi adalah $ k = \frac{1}{2}. \heartsuit $
$x_1+x_2 = \frac{-b}{a} = \frac{-[-4(k+1)]}{1} = 4(k+1) $
artinya $ x_1 + x_2 = 4(k+1) \, $ ...pers(i)
$\clubsuit \, $ Salah satu akarnya bernilai tiga kali akar yang lainnya
$ x_1 = 3x_2 \, $ ....pers(ii)
$\clubsuit \, $ Substitusi $ x_1 = 3x_2 \, $ ke pers(i)
$ x_1 + x_2 = 4(k+1) \rightarrow 3x_2 + x_2 = 4(k+1) \rightarrow x_2 = k+1 $
$\clubsuit \, $ Substitusi $ x_2 = k+1 \, $ ke PK
$\begin{align} x^2-4(k+1)x+k^2-k+7 & =0 \\ (k+1)^2-4(k+1)(k+1)+k^2-k+7 & =0 \\ 2k^2 + 7k - 4 & = 0 \\ (2k-1)(k+4) & = 0 \\ k = \frac{1}{2} \vee k & = -4 \end{align}$
$\clubsuit \, $ Semua akar-akarnya lebih dari 2
$\begin{align} x_1 > 2 \text{ dan } x_2 & > 2 \\ \text{Jumlahkan keduanya } & \\ x_1 + x_2 & > 2 + 2 \\ x_1 + x_2 & > 4 \\ 4(k+1) & > 4 \\ k+1 & > 1 \\ k & > 0 \end{align}$
Karena nilai $ k > 0 \, $ , maka yang memenuhi adalah $ k = \frac{1}{2} $
Jadi, nilai $ k \, $ yang memenuhi adalah $ k = \frac{1}{2}. \heartsuit $
Nomor 2
Diketahui $f(x)=\frac{x^2-4}{g(x)}+3 , \, h(x)=\frac{g(x)+3}{x+1}, $
$ m(x)=\frac{h(x)-2}{x-1}; \, x\neq 1 ; m(1)=2014.$
Jika $f(x)$ dibagi $x^2+x-2$ memiliki sisa $ax+b$ , maka nilai $a+2b=...$
$ m(x)=\frac{h(x)-2}{x-1}; \, x\neq 1 ; m(1)=2014.$
Jika $f(x)$ dibagi $x^2+x-2$ memiliki sisa $ax+b$ , maka nilai $a+2b=...$
$\spadesuit \, $ Nilai $ m(1) = 2014 \, $ (untuk $ x = 1 $) dan $ m(x)=\frac{h(x)-2}{x-1} \, $ tidak boleh untuk $ x = 1 \, $
, maka haruslah $ h(x) - 2 \, $ memeiliki faktor $ (x-1) \, $, sehingga
$\begin{align} h(x) - 2 & = (x-1) .k(x) \\ h(x) & = (x-1).k(x) + 2 \, \, \, \text{....pers(i)} \end{align}$
dengan $ k(x) \, $ suatu fungsi tertentu (polinomial)
$\spadesuit \, $ Substitusi $ x = 1 \, $ ke pers(i)
$\begin{align} x=1 \rightarrow h(x) & = (x-1).k(x) + 2 \\ h(1) & = (1-1).k(1) + 2 \\ h(1) & = 2 \end{align}$
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ h(1) = 2 $
$\begin{align} x=1 \rightarrow h(x) & =\frac{g(x)+3}{x+1} \\ h(1) & =\frac{g(1)+3}{1+1} \\ 2 & =\frac{g(1)+3}{2} \\ g(1) & = 1 \end{align}$
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ g(1) = 1 $
$\begin{align} x=1 \rightarrow f(x) & =\frac{x^2-4}{g(x)}+3 \\ f(1) & =\frac{1^2-4}{g(1)}+3 \\ f(1) & =\frac{-3}{g(1)}+3 \\ f(1) & = 0 \end{align}$
$\spadesuit \, $ Substitusi $ x = -2 \, $
$\begin{align} x=-2 \rightarrow f(x) & =\frac{x^2-4}{g(x)}+3 \\ f(-2) & =\frac{(-2)^2-4}{g(-2)}+3 \\ f(-2) & =\frac{4-4}{g(-2)}+3 \\ f(-2) & = 3 \end{align}$
Diperoleh $ f(1) = 0 \, $ dan $ f(-2) = 3 $
$\spadesuit \, $ Fungsi $ f(x) \, $ dibagi $ x^2 + x -2 \, $ sisanya $ ax+b \, $ dan anggap hasilnya $ z(x) $ , dapat ditulis
$ f(x) = (x^2 + x - 2).z(x) + (ax+b) \, $ ....pers(ii)
atau $ f(x) = (x-1)(x+2).z(x) + (ax+b) \, $ ....pers(ii)
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ x=-2 \, $ ke pers(ii)
$\begin{align} x=1 \rightarrow f(x) & = (x-1)(x+2).z(x) + (ax+b) \\ f(1) & = (1-1)(1+2).z(1) + (a.1+b) \\ 0 & = a + b \, \, \text{...pers(iii)} \\ x=-2 \rightarrow f(x) & = (x-1)(x+2).z(x) + (ax+b) \\ f(-2) & = (-2-1)(-2+2).z(-2) + (a.(-2)+b) \\ 3 & = -2a + b \, \, \text{...pers(iv)} \end{align}$
$\spadesuit \, $ Eliminasi pers(iii) dan pers(iv)
$\begin{array}{cc} a+b = 0 & \\ -2a+b = 3 & - \\ \hline 3a = -3 & \\ a = -1 & \end{array} $
pers(iii) : $ a+b = 0 \rightarrow -1 + b = 0 \rightarrow b = 1 $
Sehingga nilai $ a + 2b = -1 + 2.1 = -1 + 2 = 1 $
Jadi, nilai $ a + 2b = 1 . \heartsuit $
$\begin{align} h(x) - 2 & = (x-1) .k(x) \\ h(x) & = (x-1).k(x) + 2 \, \, \, \text{....pers(i)} \end{align}$
dengan $ k(x) \, $ suatu fungsi tertentu (polinomial)
$\spadesuit \, $ Substitusi $ x = 1 \, $ ke pers(i)
$\begin{align} x=1 \rightarrow h(x) & = (x-1).k(x) + 2 \\ h(1) & = (1-1).k(1) + 2 \\ h(1) & = 2 \end{align}$
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ h(1) = 2 $
$\begin{align} x=1 \rightarrow h(x) & =\frac{g(x)+3}{x+1} \\ h(1) & =\frac{g(1)+3}{1+1} \\ 2 & =\frac{g(1)+3}{2} \\ g(1) & = 1 \end{align}$
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ g(1) = 1 $
$\begin{align} x=1 \rightarrow f(x) & =\frac{x^2-4}{g(x)}+3 \\ f(1) & =\frac{1^2-4}{g(1)}+3 \\ f(1) & =\frac{-3}{g(1)}+3 \\ f(1) & = 0 \end{align}$
$\spadesuit \, $ Substitusi $ x = -2 \, $
$\begin{align} x=-2 \rightarrow f(x) & =\frac{x^2-4}{g(x)}+3 \\ f(-2) & =\frac{(-2)^2-4}{g(-2)}+3 \\ f(-2) & =\frac{4-4}{g(-2)}+3 \\ f(-2) & = 3 \end{align}$
Diperoleh $ f(1) = 0 \, $ dan $ f(-2) = 3 $
$\spadesuit \, $ Fungsi $ f(x) \, $ dibagi $ x^2 + x -2 \, $ sisanya $ ax+b \, $ dan anggap hasilnya $ z(x) $ , dapat ditulis
$ f(x) = (x^2 + x - 2).z(x) + (ax+b) \, $ ....pers(ii)
atau $ f(x) = (x-1)(x+2).z(x) + (ax+b) \, $ ....pers(ii)
$\spadesuit \, $ Substitusi $ x = 1 \, $ dan $ x=-2 \, $ ke pers(ii)
$\begin{align} x=1 \rightarrow f(x) & = (x-1)(x+2).z(x) + (ax+b) \\ f(1) & = (1-1)(1+2).z(1) + (a.1+b) \\ 0 & = a + b \, \, \text{...pers(iii)} \\ x=-2 \rightarrow f(x) & = (x-1)(x+2).z(x) + (ax+b) \\ f(-2) & = (-2-1)(-2+2).z(-2) + (a.(-2)+b) \\ 3 & = -2a + b \, \, \text{...pers(iv)} \end{align}$
$\spadesuit \, $ Eliminasi pers(iii) dan pers(iv)
$\begin{array}{cc} a+b = 0 & \\ -2a+b = 3 & - \\ \hline 3a = -3 & \\ a = -1 & \end{array} $
pers(iii) : $ a+b = 0 \rightarrow -1 + b = 0 \rightarrow b = 1 $
Sehingga nilai $ a + 2b = -1 + 2.1 = -1 + 2 = 1 $
Jadi, nilai $ a + 2b = 1 . \heartsuit $
Nomor 3
Himpunan semua bilangan $x$ yang memenuhi pertidaksamaan $\frac{1}{\sqrt{x+1}-\sqrt{x}}\leq \sqrt{2x+5}$ adalah ...
$\clubsuit \, $ Karena nilai $ \sqrt{x+1} \, $ tidak akan sama dengan nilai $ \sqrt{x} \, $ (dua bilangan berurutan tidak akan pernah
sama nilainya), maka pasti nilai $ \sqrt{x+1} - \sqrt{x} \neq 0 \, $ , sehingga bisa dirasionalkan bentuk pecahannya dan tidak akan
mengurangi akar-akarnya karena penyebutnya yang hilang.
$\clubsuit \, $ Rasionalkan ruas kiri
$\begin{align} \frac{1}{\sqrt{x+1}-\sqrt{x}} & \leq \sqrt{2x+5} \\ \frac{1}{\sqrt{x+1}-\sqrt{x}} . \frac{\sqrt{x+1}+ \sqrt{x}}{\sqrt{x+1}+ \sqrt{x}} & \leq \sqrt{2x+5} \\ \frac{\sqrt{x+1}+ \sqrt{x}}{(x+1)-(x)} & \leq \sqrt{2x+5} \\ \sqrt{x+1}+ \sqrt{x} & \leq \sqrt{2x+5} \end{align}$
$\clubsuit \, $ Kuadratkan kedua ruas
$\begin{align} (\sqrt{x+1}+ \sqrt{x})^2 & \leq (\sqrt{2x+5})^2 \\ (x+1)+x+2\sqrt{x^2+x} & \leq 2x + 5 \\ \sqrt{x^2+x} & \leq 2 \, \, \, \text{(kuadratkan lagi)} \\ x^2 + x & \leq 4 \\ x^2 + x - 4 & \leq 0 \\ x_{1,2} & = \frac{-1 \pm \sqrt{17}}{2} \end{align}$

HP1 = $ \left\{ \frac{-1 - \sqrt{17}}{2} \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} $
$\clubsuit \, $ Menentukan syarat-syarat akar
*). $\sqrt{x+1} \, $ syaratnya : $ x + 1 \geq 0 \rightarrow x \geq -1 $
*). $\sqrt{x} \, $ syaratnya : $ x \geq 0 $
*). $\sqrt{2x+5} \, $ syaratnya : $ 2x+5 \geq 0 \rightarrow x \geq \frac{-5}{2} $
Syarat yang memenuhi ketiganya adalah : HP2 = $ \{ x \geq 0 \} $
Sehingga solusinya : HP = HP1 $\cap $ HP2 = $ \left\{ 0 \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} $
Jadi, solusinya HP = $ \left\{ 0 \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} . \heartsuit $
$\clubsuit \, $ Rasionalkan ruas kiri
$\begin{align} \frac{1}{\sqrt{x+1}-\sqrt{x}} & \leq \sqrt{2x+5} \\ \frac{1}{\sqrt{x+1}-\sqrt{x}} . \frac{\sqrt{x+1}+ \sqrt{x}}{\sqrt{x+1}+ \sqrt{x}} & \leq \sqrt{2x+5} \\ \frac{\sqrt{x+1}+ \sqrt{x}}{(x+1)-(x)} & \leq \sqrt{2x+5} \\ \sqrt{x+1}+ \sqrt{x} & \leq \sqrt{2x+5} \end{align}$
$\clubsuit \, $ Kuadratkan kedua ruas
$\begin{align} (\sqrt{x+1}+ \sqrt{x})^2 & \leq (\sqrt{2x+5})^2 \\ (x+1)+x+2\sqrt{x^2+x} & \leq 2x + 5 \\ \sqrt{x^2+x} & \leq 2 \, \, \, \text{(kuadratkan lagi)} \\ x^2 + x & \leq 4 \\ x^2 + x - 4 & \leq 0 \\ x_{1,2} & = \frac{-1 \pm \sqrt{17}}{2} \end{align}$

HP1 = $ \left\{ \frac{-1 - \sqrt{17}}{2} \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} $
$\clubsuit \, $ Menentukan syarat-syarat akar
*). $\sqrt{x+1} \, $ syaratnya : $ x + 1 \geq 0 \rightarrow x \geq -1 $
*). $\sqrt{x} \, $ syaratnya : $ x \geq 0 $
*). $\sqrt{2x+5} \, $ syaratnya : $ 2x+5 \geq 0 \rightarrow x \geq \frac{-5}{2} $
Syarat yang memenuhi ketiganya adalah : HP2 = $ \{ x \geq 0 \} $
Sehingga solusinya : HP = HP1 $\cap $ HP2 = $ \left\{ 0 \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} $
Jadi, solusinya HP = $ \left\{ 0 \leq x \leq \frac{-1 + \sqrt{17}}{2} \right\} . \heartsuit $
Nomor 4
A dan B berdiri saling berhadapan dengan jarak 100 m. Seekor kucing bediri di samping A dan mulai berlari menuju B dengan kecepatan 2 m/s.
Pada saat yang sama, A berjalan menuju B dengan kecepatan 1 m/s dan berhenti ketika kucing tiba di B. Kucing lalu berbalik arah dan berlari menuju A
dengan kecepatan yang sama. B tidak bergerak dari posisi awal. Kemudian, kucing dan A kembali menuju B dengan kecepatannya masing-masing. Jika proses ini
berlanjut terus-menerus, jarak yang ditempuh oleh kucing adalah ... m.
$\spadesuit \, $ Konsep geometri tak hingga : $ S_\infty = \frac{a}{1-r} $
$\spadesuit \, $ Misal, Misal $ S_A \, $ = jarak A yang ditempuh
dan $ S_k \, $ = jarak kucing yang ditempuh.
Rumus jarak : $ S = V . t \, $ dengan $ V \, $ jarak dan $ t \, $ adalah waktu.
$V_k = 2 \, $ m/s dan $ V_A = 1 \, $ m/s , artinya jarak yang ditempuh oleh A separuh dari jarak yang ditempuh oleh kucing. Berikut ilustrasi pergerakan kucing dan A .

$\spadesuit \, $ Menentukan total jarak yang ditempuh kucing
Dari ilustrasi gambar di atas, jarak total yang ditempuh kucing : $\begin{align} S_k & = 100 + 50 + 50 + 25 + 25 + \frac{25}{2} + \frac{25}{2} + .... \\ & = 100 + 2(50 + 25 + \frac{25}{2} + ..... ) \\ & = 100 + 2(S_\infty ) \\ & = 100 + 2(\frac{a}{1-r} ) \\ & = 100 + 2(\frac{50}{1-\frac{1}{2}} ) \\ & = 100 + 2(\frac{50}{\frac{1}{2}} ) \\ & = 100 + 2(100 ) \\ & = 100 + 200 = 300 \end{align}$
Jadi, total jarak yang ditempuh oleh kucing adalah 300 m. $ \heartsuit $
$\spadesuit \, $ Misal, Misal $ S_A \, $ = jarak A yang ditempuh
dan $ S_k \, $ = jarak kucing yang ditempuh.
Rumus jarak : $ S = V . t \, $ dengan $ V \, $ jarak dan $ t \, $ adalah waktu.
$V_k = 2 \, $ m/s dan $ V_A = 1 \, $ m/s , artinya jarak yang ditempuh oleh A separuh dari jarak yang ditempuh oleh kucing. Berikut ilustrasi pergerakan kucing dan A .

$\spadesuit \, $ Menentukan total jarak yang ditempuh kucing
Dari ilustrasi gambar di atas, jarak total yang ditempuh kucing : $\begin{align} S_k & = 100 + 50 + 50 + 25 + 25 + \frac{25}{2} + \frac{25}{2} + .... \\ & = 100 + 2(50 + 25 + \frac{25}{2} + ..... ) \\ & = 100 + 2(S_\infty ) \\ & = 100 + 2(\frac{a}{1-r} ) \\ & = 100 + 2(\frac{50}{1-\frac{1}{2}} ) \\ & = 100 + 2(\frac{50}{\frac{1}{2}} ) \\ & = 100 + 2(100 ) \\ & = 100 + 200 = 300 \end{align}$
Jadi, total jarak yang ditempuh oleh kucing adalah 300 m. $ \heartsuit $
Nomor 5
Diketahui vektor $\vec{a}=(-1,1,2) , \vec{u}=(-1,c,2)$ dan $\vec{x}=(-3,0,1)$. $L_1$ adalah luas segitiga siku-siku yang dibentuk oleh $\vec{a}$
dan proyeksi vektor $\vec{a}$ pada $\vec{x}$. $L_2$ adalah luas segitiga siku-siku yang dibentuk oleh $\vec{u}$ dan proyeksi vektor $\vec{u}$ pada $\vec{x}$.
Jika $L_1=\frac{1}{8}L_2$, maka nilai $2c^2=...$
$\clubsuit \, $ Menentukan panjang dan perkalian dot
$\vec{a}=(-1,1,2) , \vec{u}=(-1,c,2) \, \, \, \, $ dan $\vec{x}=(-3,0,1)$
$ |\vec{a}| = \sqrt{(-1)^2 + 1^2 + 2^2 } = \sqrt{6} $
$ |\vec{u}| = \sqrt{(-1)^2 + c^2 + 2^2 } = \sqrt{c^2 + 5} $
$ |\vec{x}| = \sqrt{(-3)^2 + 0^2 + 1^2 } = \sqrt{10} $
$ \vec{a} . \vec{x} = (-1).(-3) + 1.0 + 2.1 = 3 + 0 + 2 = 5 $
$ \vec{u} . \vec{x} = (-1).(-3) + c.0 + 2.1 = 3 + 0 + 2 = 5 $
$\clubsuit \, $ Konsep proyeksi skalar vektor (panjangnya)

Proyeksi skalar $ \vec{a} \, $ pada $ \vec{x} \, $ adalah $ \vec{c} \, $ dengan panjangnya : $|\vec{c}| = \frac{\vec{a}.\vec{x}}{|\vec{x}|} $
$\clubsuit \, $ Proyeksi $ \vec{a} \, $ pada $ \vec{x} \, $ dan luasnya
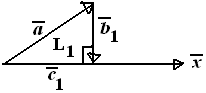
$ |\vec{c_1}| = \frac{\vec{a}.\vec{x}}{|\vec{x}|} = \frac{5}{\sqrt{10}} = \frac{\sqrt{10}}{2} $
Dengan pythagoras :
$ |\vec{b_1}| = \sqrt{|\vec{a}|^2 - |\vec{c_1}|^2} = \sqrt{(\sqrt{6})^2 - (\frac{\sqrt{10}}{2})^2}= \frac{1}{2}\sqrt{14} $
$L_1 = \frac{1}{2}. |\vec{c_1}| . |\vec{b_1}| = \frac{1}{2}. \frac{\sqrt{10}}{2} . \frac{1}{2}\sqrt{14} = \frac{\sqrt{35}}{4} $
$\clubsuit \, $ Proyeksi $ \vec{u} \, $ pada $ \vec{x} \, $ dan luasnya
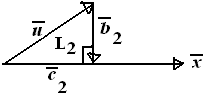
$ |\vec{c_2}| = \frac{\vec{u}.\vec{x}}{|\vec{x}|} = \frac{5}{\sqrt{10}} = \frac{\sqrt{10}}{2} $
Dengan pythagoras :
$ |\vec{b_2}| = \sqrt{|\vec{u}|^2 - |\vec{c_2}|^2} = \sqrt{(\sqrt{c^2 + 5})^2 - (\frac{\sqrt{10}}{2})^2}= \frac{\sqrt{2}.\sqrt{5+2c^2}}{2} $
$L_2 = \frac{1}{2}. |\vec{c_2}| . |\vec{b_2}| = \frac{1}{2}. \frac{\sqrt{10}}{2} . \frac{\sqrt{2}.\sqrt{5+2c^2}}{2} = \frac{\sqrt{5(5+2c^2)}}{4} $
$\clubsuit \, $ Menentukan nilai $ 2c^2 $
$\begin{align} L_1 & =\frac{1}{8}L_2 \\ \frac{\sqrt{35}}{4} & =\frac{1}{8} . \frac{\sqrt{5(5+2c^2)}}{4} \\ \sqrt{35} & = \frac{\sqrt{5(5+2c^2)}}{8} \, \, \, \text{(kuadratkan)} \\ 35 & = \frac{5(5+2c^2)}{64} \, \, \, \text{(bagi 5)} \\ 7 & = \frac{(5+2c^2)}{64} \\ 5+2c^2 & = 7 . 64 \\ 5+2c^2 & = 448 \\ 2c^2 & = 443 \end{align}$
Jadi, nilai $ 2c^2 = 443 . \heartsuit $
$\vec{a}=(-1,1,2) , \vec{u}=(-1,c,2) \, \, \, \, $ dan $\vec{x}=(-3,0,1)$
$ |\vec{a}| = \sqrt{(-1)^2 + 1^2 + 2^2 } = \sqrt{6} $
$ |\vec{u}| = \sqrt{(-1)^2 + c^2 + 2^2 } = \sqrt{c^2 + 5} $
$ |\vec{x}| = \sqrt{(-3)^2 + 0^2 + 1^2 } = \sqrt{10} $
$ \vec{a} . \vec{x} = (-1).(-3) + 1.0 + 2.1 = 3 + 0 + 2 = 5 $
$ \vec{u} . \vec{x} = (-1).(-3) + c.0 + 2.1 = 3 + 0 + 2 = 5 $
$\clubsuit \, $ Konsep proyeksi skalar vektor (panjangnya)

Proyeksi skalar $ \vec{a} \, $ pada $ \vec{x} \, $ adalah $ \vec{c} \, $ dengan panjangnya : $|\vec{c}| = \frac{\vec{a}.\vec{x}}{|\vec{x}|} $
$\clubsuit \, $ Proyeksi $ \vec{a} \, $ pada $ \vec{x} \, $ dan luasnya

$ |\vec{c_1}| = \frac{\vec{a}.\vec{x}}{|\vec{x}|} = \frac{5}{\sqrt{10}} = \frac{\sqrt{10}}{2} $
Dengan pythagoras :
$ |\vec{b_1}| = \sqrt{|\vec{a}|^2 - |\vec{c_1}|^2} = \sqrt{(\sqrt{6})^2 - (\frac{\sqrt{10}}{2})^2}= \frac{1}{2}\sqrt{14} $
$L_1 = \frac{1}{2}. |\vec{c_1}| . |\vec{b_1}| = \frac{1}{2}. \frac{\sqrt{10}}{2} . \frac{1}{2}\sqrt{14} = \frac{\sqrt{35}}{4} $
$\clubsuit \, $ Proyeksi $ \vec{u} \, $ pada $ \vec{x} \, $ dan luasnya

$ |\vec{c_2}| = \frac{\vec{u}.\vec{x}}{|\vec{x}|} = \frac{5}{\sqrt{10}} = \frac{\sqrt{10}}{2} $
Dengan pythagoras :
$ |\vec{b_2}| = \sqrt{|\vec{u}|^2 - |\vec{c_2}|^2} = \sqrt{(\sqrt{c^2 + 5})^2 - (\frac{\sqrt{10}}{2})^2}= \frac{\sqrt{2}.\sqrt{5+2c^2}}{2} $
$L_2 = \frac{1}{2}. |\vec{c_2}| . |\vec{b_2}| = \frac{1}{2}. \frac{\sqrt{10}}{2} . \frac{\sqrt{2}.\sqrt{5+2c^2}}{2} = \frac{\sqrt{5(5+2c^2)}}{4} $
$\clubsuit \, $ Menentukan nilai $ 2c^2 $
$\begin{align} L_1 & =\frac{1}{8}L_2 \\ \frac{\sqrt{35}}{4} & =\frac{1}{8} . \frac{\sqrt{5(5+2c^2)}}{4} \\ \sqrt{35} & = \frac{\sqrt{5(5+2c^2)}}{8} \, \, \, \text{(kuadratkan)} \\ 35 & = \frac{5(5+2c^2)}{64} \, \, \, \text{(bagi 5)} \\ 7 & = \frac{(5+2c^2)}{64} \\ 5+2c^2 & = 7 . 64 \\ 5+2c^2 & = 448 \\ 2c^2 & = 443 \end{align}$
Jadi, nilai $ 2c^2 = 443 . \heartsuit $
