Nomor 21
Akar - akar persamaan $ x^2 - 10x = - \frac{1}{4} \, \, $ adalah $\alpha \, $ dan $\beta \, $ , maka $\sqrt{\alpha} + \sqrt{\beta} = .... $
$\spadesuit \, $ Operasi akar - akar
$\alpha + \beta = \frac{-b}{a} = \frac{-(-10)}{1} = 10 $
$\alpha . \beta = \frac{c}{a} = \frac{\frac{1}{4}}{1} = \frac{1}{4} $
$\spadesuit \, $ Soal dikuadratkan
$\begin{align} (\sqrt{\alpha} + \sqrt{\beta})^2 & = (\alpha + \beta) + 2\sqrt{\alpha . \beta} \\ & = (10) + 2\sqrt{\frac{1}{4} } \\ & = (10) + 2.\frac{1}{2} \\ & = 10 + 1 \\ (\sqrt{\alpha} + \sqrt{\beta})^2 & = 11 \\ \sqrt{\alpha} + \sqrt{\beta} & = \sqrt{11} \end{align}$
Jadi, nilai $ \sqrt{\alpha} + \sqrt{\beta} = \sqrt{11} . \heartsuit $
$\alpha + \beta = \frac{-b}{a} = \frac{-(-10)}{1} = 10 $
$\alpha . \beta = \frac{c}{a} = \frac{\frac{1}{4}}{1} = \frac{1}{4} $
$\spadesuit \, $ Soal dikuadratkan
$\begin{align} (\sqrt{\alpha} + \sqrt{\beta})^2 & = (\alpha + \beta) + 2\sqrt{\alpha . \beta} \\ & = (10) + 2\sqrt{\frac{1}{4} } \\ & = (10) + 2.\frac{1}{2} \\ & = 10 + 1 \\ (\sqrt{\alpha} + \sqrt{\beta})^2 & = 11 \\ \sqrt{\alpha} + \sqrt{\beta} & = \sqrt{11} \end{align}$
Jadi, nilai $ \sqrt{\alpha} + \sqrt{\beta} = \sqrt{11} . \heartsuit $
Nomor 22
Jika $ y = \left| \begin{matrix} x^2-1 & 2 \\ 4x & x+3 \end{matrix} \right| \, \, $ maka nilai minimum $y \, $
adalah ....
$\clubsuit \, $ Menentukan determinan : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow |A| = ad-bc $
$\begin{align} y & = \left| \begin{matrix} x^2-1 & 2 \\ 4x & x+3 \end{matrix} \right| \\ y & = (x^2-1).(x+3) - 8x \\ y & = x^3 + 3x^2 -9x - 3 \\ y^\prime & = 3x^2 + 6x - 9 \, \, \text{(turunannya)} \end{align}$
$\clubsuit \, $ Nilai maks/min : $ y^\prime = 0 \, \, $ (turunan = 0)
$\begin{align} y^\prime & = 0 \\ 3x^2 + 6x - 9 & = 0 \, \, \text{(bagi 3)} \\ x^2 + 2x - 3 & = 0 \\ (x-1)(x+3) & = 0 \\ x=1 & \vee x =-3 \end{align}$
$\clubsuit \, $ Substitusi nilai $x \, $ ke $\, y = x^3 + 3x^2 -9x - 3 $
$ x = 1 \rightarrow y = 1^3 + 3.1^2 -9.1 - 3 = -8 $
$ x = -3 \rightarrow y = (-3)^3 + 3.(-3)^2 -9.(-3) - 3 = 24 $
Jadi, nilai minimumnya adalah -8 . $ \heartsuit $
$\begin{align} y & = \left| \begin{matrix} x^2-1 & 2 \\ 4x & x+3 \end{matrix} \right| \\ y & = (x^2-1).(x+3) - 8x \\ y & = x^3 + 3x^2 -9x - 3 \\ y^\prime & = 3x^2 + 6x - 9 \, \, \text{(turunannya)} \end{align}$
$\clubsuit \, $ Nilai maks/min : $ y^\prime = 0 \, \, $ (turunan = 0)
$\begin{align} y^\prime & = 0 \\ 3x^2 + 6x - 9 & = 0 \, \, \text{(bagi 3)} \\ x^2 + 2x - 3 & = 0 \\ (x-1)(x+3) & = 0 \\ x=1 & \vee x =-3 \end{align}$
$\clubsuit \, $ Substitusi nilai $x \, $ ke $\, y = x^3 + 3x^2 -9x - 3 $
$ x = 1 \rightarrow y = 1^3 + 3.1^2 -9.1 - 3 = -8 $
$ x = -3 \rightarrow y = (-3)^3 + 3.(-3)^2 -9.(-3) - 3 = 24 $
Jadi, nilai minimumnya adalah -8 . $ \heartsuit $
Nomor 23
$\sqrt{\frac{3}{9^p}\sqrt{\frac{9^p}{3}}} = 27, \, \, $ nilai $ p = .... $
$\spadesuit \, $ Sifat-sifat eksponen :
$\frac{a^m}{a^n} = a^{m-n}, \, a^m.a^n=a^{m+n}, \, (a^m)^n = a^{m.n} $
$a^{f(x)} = a^{g(x)} \rightarrow f(x) = g(x) $
$\spadesuit \, $ Menentukan nilai $ \, p $
$\begin{align} \sqrt{\frac{3}{9^p}\sqrt{\frac{9^p}{3}}} & = 27 \leftrightarrow \left[ \frac{3}{9^p} . \left( \frac{9^p}{3} \right)^\frac{1}{2} \right]^\frac{1}{2} = 3^3 \\ \left[ \left( \frac{9^p}{3} \right)^{-1} . \left( \frac{9^p}{3} \right)^\frac{1}{2} \right]^\frac{1}{2} & = 3^3 \leftrightarrow \left[ \left( \frac{9^p}{3} \right)^{-1+ \frac{1}{2} } \right]^\frac{1}{2} = 3^3 \\ \left[ \left( \frac{9^p}{3} \right)^{-\frac{1}{2} } \right]^\frac{1}{2} & = 3^3 \leftrightarrow \left( \frac{9^p}{3} \right)^{-\frac{1}{4} } = 3^3 \\ \left( \frac{3^{2p}}{3^1} \right)^{-\frac{1}{4} } & = 3^3 \leftrightarrow \left( 3^{2p-1} \right)^{-\frac{1}{4} } = 3^3 \\ 3^\frac{-(2p-1)}{4} & = 3^3 \leftrightarrow \frac{-(2p-1)}{4} = 3 \\ 1-2p & = 12 \leftrightarrow p = \frac{-11}{2} \leftrightarrow p = -5\frac{1}{2} \end{align}$
Jadi, nilai $ p = -5\frac{1}{2} . \heartsuit $
$\frac{a^m}{a^n} = a^{m-n}, \, a^m.a^n=a^{m+n}, \, (a^m)^n = a^{m.n} $
$a^{f(x)} = a^{g(x)} \rightarrow f(x) = g(x) $
$\spadesuit \, $ Menentukan nilai $ \, p $
$\begin{align} \sqrt{\frac{3}{9^p}\sqrt{\frac{9^p}{3}}} & = 27 \leftrightarrow \left[ \frac{3}{9^p} . \left( \frac{9^p}{3} \right)^\frac{1}{2} \right]^\frac{1}{2} = 3^3 \\ \left[ \left( \frac{9^p}{3} \right)^{-1} . \left( \frac{9^p}{3} \right)^\frac{1}{2} \right]^\frac{1}{2} & = 3^3 \leftrightarrow \left[ \left( \frac{9^p}{3} \right)^{-1+ \frac{1}{2} } \right]^\frac{1}{2} = 3^3 \\ \left[ \left( \frac{9^p}{3} \right)^{-\frac{1}{2} } \right]^\frac{1}{2} & = 3^3 \leftrightarrow \left( \frac{9^p}{3} \right)^{-\frac{1}{4} } = 3^3 \\ \left( \frac{3^{2p}}{3^1} \right)^{-\frac{1}{4} } & = 3^3 \leftrightarrow \left( 3^{2p-1} \right)^{-\frac{1}{4} } = 3^3 \\ 3^\frac{-(2p-1)}{4} & = 3^3 \leftrightarrow \frac{-(2p-1)}{4} = 3 \\ 1-2p & = 12 \leftrightarrow p = \frac{-11}{2} \leftrightarrow p = -5\frac{1}{2} \end{align}$
Jadi, nilai $ p = -5\frac{1}{2} . \heartsuit $
Nomor 24
Diketahui $\tan x = 2,4 \, \, $ dengan $x \, \, $ dalam selang $\left[ \pi , \, \frac{3\pi}{2} \right] \, $ , maka $ \cos x = .... $
$\clubsuit \,$ Menyederhanakan nilai tan
$\tan x = 2,4=\frac{24}{10} = \frac{12}{5} = \frac{de}{sa}$
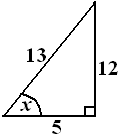
karena $x \, $ ada di kuadran III, maka nilai cos negatif.
sehingga : $\cos x = -\frac{5}{13} $
Jadi, nilai $ \cos x = -\frac{5}{13} . \heartsuit $
$\tan x = 2,4=\frac{24}{10} = \frac{12}{5} = \frac{de}{sa}$

karena $x \, $ ada di kuadran III, maka nilai cos negatif.
sehingga : $\cos x = -\frac{5}{13} $
Jadi, nilai $ \cos x = -\frac{5}{13} . \heartsuit $
Nomor 25
Nilai maksimum $f(x,y) = 3x+4y \, $ di daerah yang diarsir adalah ....
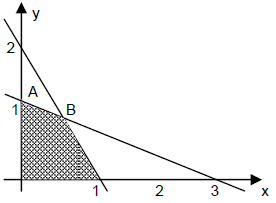

$\spadesuit \, $ Menentukan persamaan garis
garis I : melalui titik (0,1) dan (3,0)
persamaannya : $x+3y=3$
garis II : melalui titik (0,2) dan (1,0)
persamaannya : $2x+y=2$
Eliminasi pers(I) dan pers(II)
$\begin{array}{c|c|cc} x+3y=3 & \times 2 & 2x + 6y = 6 & \\ 2x+y=2 & \times 1 & 2x+y=2 & - \\ \hline & & 5y = 4 \rightarrow y = \frac{4}{5} \end{array}$
pers(I) : $x+3y=3 \rightarrow x+3.\frac{4}{5} = 3 \rightarrow x=\frac{3}{5} $
sehingga titik B $(\frac{3}{5}, \, \frac{4}{5})$
$\spadesuit \, $ Substitusi semua titik pojok ke $f(x,y) = 3x+4y $
A(0,1) $\rightarrow f = 3.0 + 4.1 = 4 $
B$(\frac{3}{5}, \, \frac{4}{5})$ $\rightarrow f = 3.\frac{3}{5} + 4.\frac{4}{5} = 5 $
A(1,0) $\rightarrow f = 3.1 + 4.0 = 3 $
Jadi, nilai maksimumnya adalah 5. $ \heartsuit $
garis I : melalui titik (0,1) dan (3,0)
persamaannya : $x+3y=3$
garis II : melalui titik (0,2) dan (1,0)
persamaannya : $2x+y=2$
Eliminasi pers(I) dan pers(II)
$\begin{array}{c|c|cc} x+3y=3 & \times 2 & 2x + 6y = 6 & \\ 2x+y=2 & \times 1 & 2x+y=2 & - \\ \hline & & 5y = 4 \rightarrow y = \frac{4}{5} \end{array}$
pers(I) : $x+3y=3 \rightarrow x+3.\frac{4}{5} = 3 \rightarrow x=\frac{3}{5} $
sehingga titik B $(\frac{3}{5}, \, \frac{4}{5})$
$\spadesuit \, $ Substitusi semua titik pojok ke $f(x,y) = 3x+4y $
A(0,1) $\rightarrow f = 3.0 + 4.1 = 4 $
B$(\frac{3}{5}, \, \frac{4}{5})$ $\rightarrow f = 3.\frac{3}{5} + 4.\frac{4}{5} = 5 $
A(1,0) $\rightarrow f = 3.1 + 4.0 = 3 $
Jadi, nilai maksimumnya adalah 5. $ \heartsuit $
Cara II
$\spadesuit \, $ Menentukan persamaan garis
garis I : melalui titik (0,1) dan (3,0)
persamaannya : $x+3y=3$
garis II : melalui titik (0,2) dan (1,0)
persamaannya : $2x+y=2$
$\spadesuit \, $ Kedua persamaan langsung dijumlahkan
$\begin{array}{cc} x+3y \leq 3 \\ 2x+y \leq 2 & + \\ \hline 3x + 4y \leq 5 & \end{array}$
artinya nilai maksimum dari $3x + 4y \, $ adalah 5.
Jadi, nilai maksimumnya adalah 5. $ \heartsuit $
$\spadesuit \, $ Menentukan persamaan garis
garis I : melalui titik (0,1) dan (3,0)
persamaannya : $x+3y=3$
garis II : melalui titik (0,2) dan (1,0)
persamaannya : $2x+y=2$
$\spadesuit \, $ Kedua persamaan langsung dijumlahkan
$\begin{array}{cc} x+3y \leq 3 \\ 2x+y \leq 2 & + \\ \hline 3x + 4y \leq 5 & \end{array}$
artinya nilai maksimum dari $3x + 4y \, $ adalah 5.
Jadi, nilai maksimumnya adalah 5. $ \heartsuit $
