Nomor 11
Jika $ A = \left[ \begin{matrix} 2 & a \\ 1 & 2 \end{matrix} \right] \, $
merupakan matriks yang mempunyai invers dan $ det(B^{-1}) = 9 , \, $ maka jumlah semua nilai $ a \, $ yang mungkin sehingga
$ det(A^{-1}) = det \left( (AB) \right) \, $
adalah .....
$\spadesuit \, $ sifat-sifat determinan
$ |A^{-1}| = \frac{1}{|A|} \, $ dan $ |A.B | = |A|.|B| $
sehigga : $ |B^{-1}| = 9 \rightarrow \frac{1}{|B|} = 9 $
$\spadesuit \, $ Menentukan nilai determinan A
$ A = \left[ \begin{matrix} 2 & a \\ 1 & 2 \end{matrix} \right] $
$ det(A) = |A| = 2.2 - a.1 = 4 - a $
$\spadesuit \, $ Menentukan nilai $ a $
$\begin{align} det(A^{-1}) & = det \left( (AB) \right) \\ |A^{-1}| & = \left| (AB) \right| \\ \frac{1}{|A|} & = |A|.|B| \\ |A|^2 & = \frac{1}{|B|} \\ (4-a)^2 & = 9 \\ 16-8a+a^2 & = 9 \\ a^2 - 8a + 7 & = 0 \\ (a-1)(a-7) & = 0 \\ a = 1 \vee a & = 7 \end{align}$
hasil jumlah nilai $ a \, $ adalah $ a_1+a_2 = 1 + 7 = 8 $
atau gunakan operasi akar-akar :
$ a^2 -8a + 7 = 0 \rightarrow a_1+a_2 = \frac{-b}{a} = \frac{-(-8)}{1} = 8 $
Jadi, hasil jumlah semua nilai $ a \, $ adalah 8. $ \heartsuit $
$ |A^{-1}| = \frac{1}{|A|} \, $ dan $ |A.B | = |A|.|B| $
sehigga : $ |B^{-1}| = 9 \rightarrow \frac{1}{|B|} = 9 $
$\spadesuit \, $ Menentukan nilai determinan A
$ A = \left[ \begin{matrix} 2 & a \\ 1 & 2 \end{matrix} \right] $
$ det(A) = |A| = 2.2 - a.1 = 4 - a $
$\spadesuit \, $ Menentukan nilai $ a $
$\begin{align} det(A^{-1}) & = det \left( (AB) \right) \\ |A^{-1}| & = \left| (AB) \right| \\ \frac{1}{|A|} & = |A|.|B| \\ |A|^2 & = \frac{1}{|B|} \\ (4-a)^2 & = 9 \\ 16-8a+a^2 & = 9 \\ a^2 - 8a + 7 & = 0 \\ (a-1)(a-7) & = 0 \\ a = 1 \vee a & = 7 \end{align}$
hasil jumlah nilai $ a \, $ adalah $ a_1+a_2 = 1 + 7 = 8 $
atau gunakan operasi akar-akar :
$ a^2 -8a + 7 = 0 \rightarrow a_1+a_2 = \frac{-b}{a} = \frac{-(-8)}{1} = 8 $
Jadi, hasil jumlah semua nilai $ a \, $ adalah 8. $ \heartsuit $
Nomor 12
Jika semua akar persamaan $ x^2 - 6x + q = 0 \, $ merupakan bilangan bulat positif, maka jumlah semua nilai $ q \, $
yang mungkin adalah .....
$\clubsuit \, $ Persamaan kuadrat : $ x^2 - 6x + q = 0 $
$ a = 1, \, b = -6 , \, $ dan $ c = q $
$\clubsuit \, $ Operasi akar-akar :
$ x_1 + x_2 = \frac{-b}{a} = \frac{-(-6)}{1} = 6 \, $ ....pers(i)
$ x_1 . x_2 = \frac{c}{a} = \frac{q}{1} = q \, $ ....pers(ii)
$\clubsuit \, $ Menentukan nilai $ q \, $ dari pers(i) dan pers(ii) dengan $ x_1 \, $ dan $ x_2 \, $ bilangan bulat positif.
$ x_1 + x_2 = 6 \, $ dan $ x_1.x_2 = q $
*). $ x_1 = 1, \, x_2 = 5 \rightarrow q = x_1.x_2 = 1.5 = 5 $
*). $ x_1 = 2, \, x_2 = 4 \rightarrow q = x_1.x_2 = 2.4 = 8 $
*). $ x_1 = 3, \, x_2 = 3 \rightarrow q = x_1.x_2 = 3.3 = 9 $
Sehingga jumlah semua nilai $ q \, $ yang mungkin :
Jumlah = 5 + 8 + 9 = 22.
Jadi, jumlah semua nilai $ q \, $ adalah 22. $ \heartsuit $
$ a = 1, \, b = -6 , \, $ dan $ c = q $
$\clubsuit \, $ Operasi akar-akar :
$ x_1 + x_2 = \frac{-b}{a} = \frac{-(-6)}{1} = 6 \, $ ....pers(i)
$ x_1 . x_2 = \frac{c}{a} = \frac{q}{1} = q \, $ ....pers(ii)
$\clubsuit \, $ Menentukan nilai $ q \, $ dari pers(i) dan pers(ii) dengan $ x_1 \, $ dan $ x_2 \, $ bilangan bulat positif.
$ x_1 + x_2 = 6 \, $ dan $ x_1.x_2 = q $
*). $ x_1 = 1, \, x_2 = 5 \rightarrow q = x_1.x_2 = 1.5 = 5 $
*). $ x_1 = 2, \, x_2 = 4 \rightarrow q = x_1.x_2 = 2.4 = 8 $
*). $ x_1 = 3, \, x_2 = 3 \rightarrow q = x_1.x_2 = 3.3 = 9 $
Sehingga jumlah semua nilai $ q \, $ yang mungkin :
Jumlah = 5 + 8 + 9 = 22.
Jadi, jumlah semua nilai $ q \, $ adalah 22. $ \heartsuit $
Nomor 13
Jika garis $ 2x-y = 3 \, $ tidak memotong maupun menyinggung kurva $ y = x^2 + ax + 1 , \, $ maka ....
$\spadesuit \, $ Konsep dasar hubungan garis dan parabola
Syarat garis dan parabola tidak berpotongan maupun menyinggung : $ D < 0 $ . dengan $ D \, $ adalah nilai Diskriminan , rumus : $ D = b^2-4ac $
$\spadesuit \, $ Substitusi parabola ke garis
$\begin{align} 2x-y & = 3 \\ 2x-(x^2 + ax + 1) & = 3 \\ -x^2 + 2x - ax - 1 & = 3 \\ -x^2 + (2-a)x - 4 & = 0 \\ a = -1, \, b = 2-a, \, c & = -4 \\ \text{ Syarat : } D & < 0 \\ b^2 - 4ac & < 0 \\ [2-a]^2 - 4.(-1).(-4) & < 0 \\ (4 - 4a + a^2) - 16 & < 0 \\ a^2 - 4a - 12 & < 0 \\ (a-6)(a+2) & < 0 \\ a = 6 \vee a & = -2 \end{align}$

Jadi, garis dan parabola tidak berpotongan maupun menyinggung ketika $ \{ -2 < a < 6 \} . \heartsuit $
Syarat garis dan parabola tidak berpotongan maupun menyinggung : $ D < 0 $ . dengan $ D \, $ adalah nilai Diskriminan , rumus : $ D = b^2-4ac $
$\spadesuit \, $ Substitusi parabola ke garis
$\begin{align} 2x-y & = 3 \\ 2x-(x^2 + ax + 1) & = 3 \\ -x^2 + 2x - ax - 1 & = 3 \\ -x^2 + (2-a)x - 4 & = 0 \\ a = -1, \, b = 2-a, \, c & = -4 \\ \text{ Syarat : } D & < 0 \\ b^2 - 4ac & < 0 \\ [2-a]^2 - 4.(-1).(-4) & < 0 \\ (4 - 4a + a^2) - 16 & < 0 \\ a^2 - 4a - 12 & < 0 \\ (a-6)(a+2) & < 0 \\ a = 6 \vee a & = -2 \end{align}$

Jadi, garis dan parabola tidak berpotongan maupun menyinggung ketika $ \{ -2 < a < 6 \} . \heartsuit $
Nomor 14
Diketahui rata-rata dari 9 nilai pengamatan sama dengan dua kali mediannya. Jika jumlah nilai pengamatan yang lebih kecil daripada median
adalah 106 dan jumlah nilai pengamatan yang lebih besar daripada median adalah 200, maka rata-rata dari 9 nilai pengamatan tersebut adalah ....
$\clubsuit \,$ Konsep rata-rata $ (\overline{X}) $
$ \overline{X} = \frac{\text{jumlah semua data}}{\text{banyak data}} $
$\clubsuit \, $ Misalkan datanya : $ a_1, a_2, a_3,a_4, x, b_1, b_2, b_3, b_4 $
dengan $ x \, $ sebagai nilai median dan
$ a_1 + a_2 + a_3 + a_4 = 106 \, $ serta $ b_1 + b_2 + b_3 + b_4 = 200 $
$\begin{align} \overline{X} & = \frac{\text{jumlah semua data}}{\text{banyak data}} \\ \overline{X} & = \frac{(a_1+a_2+a_3+a_4)+x+(b_1+b_2+b_3+b_4)}{9} \\ \overline{X} & = \frac{(106)+x+(200)}{9} \\ \overline{X} & = \frac{306+x}{9} \end{align} $
$\clubsuit \,$ Menentukan nilai $ x $
$\begin{align} \text{rata-rata } & = 2 \times \text{ median} \\ \overline{X} & = 2x \\ \frac{306+x}{9} & = 2x \\ 306 + x & = 18x \\ 17x & = 306 \\ x & = \frac{306}{17} = 18 \end{align} $
Sehingga nilai rata-ratanya : $ \overline{X} = 2x = 2. 18 = 36 $
Jadi, rata-ratanya adalah 36. $ \heartsuit $
$ \overline{X} = \frac{\text{jumlah semua data}}{\text{banyak data}} $
$\clubsuit \, $ Misalkan datanya : $ a_1, a_2, a_3,a_4, x, b_1, b_2, b_3, b_4 $
dengan $ x \, $ sebagai nilai median dan
$ a_1 + a_2 + a_3 + a_4 = 106 \, $ serta $ b_1 + b_2 + b_3 + b_4 = 200 $
$\begin{align} \overline{X} & = \frac{\text{jumlah semua data}}{\text{banyak data}} \\ \overline{X} & = \frac{(a_1+a_2+a_3+a_4)+x+(b_1+b_2+b_3+b_4)}{9} \\ \overline{X} & = \frac{(106)+x+(200)}{9} \\ \overline{X} & = \frac{306+x}{9} \end{align} $
$\clubsuit \,$ Menentukan nilai $ x $
$\begin{align} \text{rata-rata } & = 2 \times \text{ median} \\ \overline{X} & = 2x \\ \frac{306+x}{9} & = 2x \\ 306 + x & = 18x \\ 17x & = 306 \\ x & = \frac{306}{17} = 18 \end{align} $
Sehingga nilai rata-ratanya : $ \overline{X} = 2x = 2. 18 = 36 $
Jadi, rata-ratanya adalah 36. $ \heartsuit $
Nomor 15
Seorang siswa sedang melakukan percobaan statistika dengan cara menggunakan 6 bola bilyar berturut-turut bernomor 2, 3, 4, 5, 5, dan 6.
Semua bola tersebut dimasukkan ke dalam kotak. Selanjutnya, diambil tiga bola secara acak dan dicatat angka yang muncul sehingga membentuk
bilangan. Angka pada bola yang muncul pertama dicatat sebagai ratusan, angka pada bola kedua sebagai puluhan, dan angka pada bola ketiga
sebagai satuan. Jika bilangan yang sama dianggap sebagai satu kejadian dan peluang setiap kejadian adalah sama, maka peluang untuk
mendapatkan bilangan yang lebih besar daripada 600 adalah ...
$\spadesuit \, $ Konsep peluang
*). $ P(A) = \frac{n(A)}{n(S)} \, $
$\spadesuit \, $ ada 6 angka yaitu 2, 3, 4, 5, 5, dan 6.
Menentukan semua tiga angka yang terbentuk [$n(S)$] dengan membagi menjadi dua kasus :
*). Kemungkinan I : Ratusan memuat angka 5
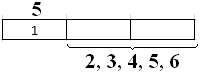
ratusannnya angka 5 sehingga ratusannya ada satu pilihan, dan sisanya angka 2, 3, 4, 5, 6 digunakan untuk mengisi angka puluhan dan satuannya. Puluhannya ada lima pilihan angka (2, 3, 4, 5, 6), dan satuannya ada empat pilihan angka tersisa.
sehingga KI = $ 1 \times 5 \times 4 = 20 $
*). Kemungkinan II : Ratusan tidak memuat angka 5
Misal ratusannya angka 2, untuk puluhannya dibagi menjadi dua kasus yaitu memuat angka 5 atau tidak

puluhan memuat angka 5 : ratusannya angka 2 ada 1 pilihan, puluhannya angka 5 ada 1 pilihan dan satuannya ada 4 pilihan (3,4,5,6)
puluhan tidak memuat angka 5 : ratusannya angka 2 ada 1 pilihan, puluhannya ada 3 pilihan (3,4,6) dan satuannya ada 3 pilihan (angka 5 dan sisanya)
sehingga untuk ratusannya angka 2 ada $ 1 \times 1 \times 4 + 1 \times 3 \times 3 = 4 + 9 = 13 $
Sementara untuk ratusannya selain angka 2 bisa juga angka lain seperti 3,4,6 , artinya ada 4 kemungkinan ratusan (2,3,4,6) yang tidak memuat angka 5.
KII = $ 4 \times 13 = 52 $
Diperoleh : $ n(S) = KI + KII = 20 + 52 = 72 $
$\spadesuit \, $ Menentukan $ n(A) \, $ [bilangan $ > 600 $ ]
Agar bilangannya lebih besar dari 600, maka ratusannya harus angka 6, kemudian angka puluhannya dibagi menjadi dua kasus yaitu memuat angka 5 atau tidak.

ratusan angka 6 ada 1 pilihan, puluhan angka 5 ada 1 pilihan, satuan ada 4 pilihan (2,3,4,5).
ratusan angka 6 ada 1 pilihan, puluhan tidak memuat angka 5 ada 3 pilihan (2,3,4), satuan ada 3 pilihan sisanya.
Sehingga $ n(A) = 1.1.4 + 1.3.3 = 4 + 9 = 13 $
Peluang kejadian A :
$ P(A) = \frac{n(A)}{n(S)} = \frac{13}{72} $
$\spadesuit \, $ Menentukan peluang $ P(A) \, $
$ P(A) = \frac{n(A)}{n(S)} = \frac{13}{72} $
Jadi, peluang terbentuknya bilangan lebih besar daripada 600 adalah $ \frac{13}{72} . \heartsuit $
*). $ P(A) = \frac{n(A)}{n(S)} \, $
$\spadesuit \, $ ada 6 angka yaitu 2, 3, 4, 5, 5, dan 6.
Menentukan semua tiga angka yang terbentuk [$n(S)$] dengan membagi menjadi dua kasus :
*). Kemungkinan I : Ratusan memuat angka 5

ratusannnya angka 5 sehingga ratusannya ada satu pilihan, dan sisanya angka 2, 3, 4, 5, 6 digunakan untuk mengisi angka puluhan dan satuannya. Puluhannya ada lima pilihan angka (2, 3, 4, 5, 6), dan satuannya ada empat pilihan angka tersisa.
sehingga KI = $ 1 \times 5 \times 4 = 20 $
*). Kemungkinan II : Ratusan tidak memuat angka 5
Misal ratusannya angka 2, untuk puluhannya dibagi menjadi dua kasus yaitu memuat angka 5 atau tidak

puluhan memuat angka 5 : ratusannya angka 2 ada 1 pilihan, puluhannya angka 5 ada 1 pilihan dan satuannya ada 4 pilihan (3,4,5,6)
puluhan tidak memuat angka 5 : ratusannya angka 2 ada 1 pilihan, puluhannya ada 3 pilihan (3,4,6) dan satuannya ada 3 pilihan (angka 5 dan sisanya)
sehingga untuk ratusannya angka 2 ada $ 1 \times 1 \times 4 + 1 \times 3 \times 3 = 4 + 9 = 13 $
Sementara untuk ratusannya selain angka 2 bisa juga angka lain seperti 3,4,6 , artinya ada 4 kemungkinan ratusan (2,3,4,6) yang tidak memuat angka 5.
KII = $ 4 \times 13 = 52 $
Diperoleh : $ n(S) = KI + KII = 20 + 52 = 72 $
$\spadesuit \, $ Menentukan $ n(A) \, $ [bilangan $ > 600 $ ]
Agar bilangannya lebih besar dari 600, maka ratusannya harus angka 6, kemudian angka puluhannya dibagi menjadi dua kasus yaitu memuat angka 5 atau tidak.

ratusan angka 6 ada 1 pilihan, puluhan angka 5 ada 1 pilihan, satuan ada 4 pilihan (2,3,4,5).
ratusan angka 6 ada 1 pilihan, puluhan tidak memuat angka 5 ada 3 pilihan (2,3,4), satuan ada 3 pilihan sisanya.
Sehingga $ n(A) = 1.1.4 + 1.3.3 = 4 + 9 = 13 $
Peluang kejadian A :
$ P(A) = \frac{n(A)}{n(S)} = \frac{13}{72} $
$\spadesuit \, $ Menentukan peluang $ P(A) \, $
$ P(A) = \frac{n(A)}{n(S)} = \frac{13}{72} $
Jadi, peluang terbentuknya bilangan lebih besar daripada 600 adalah $ \frac{13}{72} . \heartsuit $



