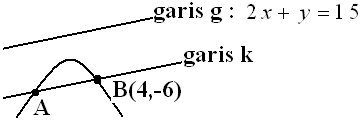Hallow sobat, bagaimana kabarnya hari ini? Semoga baik-baik saja.
pembahasan soal simak ui matematika dasar kd1 tahun 2014 nomor 11 sampai 15 ini kebanyakan membahas tentang bentuk pertidaksamaan seperti nomor 11 (tepatnya program linear), nomor 12 dan nomor 13. Untuk nomor 11 dan 12 relatif lebih mudah, sedangkan nomor 13 menurut saya bagus karena melibatkan pertidaksamaan dan persamaan yang dikombinasikan menjadi satu. pokoknya menurut saya soal nomor 13 ini keren, hahaha. Sebenarnya saya agak ragu untuk penyelesaian nomor 13 yang telah saya tulis di sini, mohon masukan dan koreksi dari sobat para pembaca ya untuk lebih menyempurnakan penyelesaiaannya. Terima kasih.
Untuk soal nomor 14 pada pembahasan soal simak ui matematika dasar kd1 tahun 2014 , menurut saya cukup menantang karena harus bisa memodifikasi bentuk aljabar dengan baik. Setelah dimisalkan seperti penyelesaiannya, ternyata mudah dalam pengerjaannya.
Nah untuk nomor 15, saya kira lebi sulit lagi, karena butuh analisa yang lebih. Mohon masukannya ya untuk penyelesaian noor 15 ini, mungkin saja ada nilai $ x $ yang lainnya selain $ x =-1 $ yang memenuhi sistem persamaan kuadrat yang ada. Terima kasih.
Ok, berikut pembahasan lengkap untuk soal simak ui matematika dasar kd1 tahun 2014 nomor 11 sampai 15. Selamat belajar.
Nomor 11

Diberikan grafik dari sistem suatu pertidaksamaan linear seperti gambar di atas. Koordinat $(x,y)$ dari titik-titik yang berada pada daerah yang diarsir memenuhi pertidaksamaan ...

Diberikan grafik dari sistem suatu pertidaksamaan linear seperti gambar di atas. Koordinat $(x,y)$ dari titik-titik yang berada pada daerah yang diarsir memenuhi pertidaksamaan ...
$\spadesuit \, $ Gambar dengan persamaannya

Dari gambar , daerah arsiran terpenuhi untuk sistem :
$x\geq 0, \, y \geq 0, \, 2x-y\geq -2, \, 3x+4y \leq 12,$
$ -x+y\geq -1, \, x+4y \geq 4 $

Dari gambar , daerah arsiran terpenuhi untuk sistem :
$x\geq 0, \, y \geq 0, \, 2x-y\geq -2, \, 3x+4y \leq 12,$
$ -x+y\geq -1, \, x+4y \geq 4 $
Nomor 12
Himpunan penyelesaian $x$ yang memenuhi pertidaksamaan $4-3x \leq x^2-4x \leq 2+6x \leq 5$ adalah ...
$\clubsuit \, $ Bentuk $\, 4-3x \leq x^2-4x \leq 2+6x \leq 5 \, $ dibagi menjadi 3 kasus
* $ 2+6x \leq 5 \, \rightarrow x \leq \frac{1}{2} \, \, $ ....(HP1)
* $ x^2-4x \leq 2+6x \rightarrow x^2 -10x -2 \leq 0 \rightarrow x = \pm \frac{10 \pm \sqrt{108}}{2} = 5 \pm 3\sqrt{3} $

HP2 = $\{ 5 - 3\sqrt{3} \leq x \leq 5 + 3\sqrt{3} \} $
* $ 4-3x \leq x^2-4x \rightarrow x^2 -x -4 \geq 0 \rightarrow x = \pm \frac{1 \pm \sqrt{17}}{2} $

HP3 = $\{ x \leq \frac{1-\sqrt{17}}{2} \vee x \geq \frac{1+\sqrt{17}}{2} \} $
Sehingga solusinya :
HP = $HP1 \cap HP2 \cap HP3 = \{ \, \} \, $ (himpunan kosong).
Jadi, penyelesaiannya adalah $ HP = \{ \, \} . \heartsuit $
* $ 2+6x \leq 5 \, \rightarrow x \leq \frac{1}{2} \, \, $ ....(HP1)
* $ x^2-4x \leq 2+6x \rightarrow x^2 -10x -2 \leq 0 \rightarrow x = \pm \frac{10 \pm \sqrt{108}}{2} = 5 \pm 3\sqrt{3} $

HP2 = $\{ 5 - 3\sqrt{3} \leq x \leq 5 + 3\sqrt{3} \} $
* $ 4-3x \leq x^2-4x \rightarrow x^2 -x -4 \geq 0 \rightarrow x = \pm \frac{1 \pm \sqrt{17}}{2} $

HP3 = $\{ x \leq \frac{1-\sqrt{17}}{2} \vee x \geq \frac{1+\sqrt{17}}{2} \} $
Sehingga solusinya :
HP = $HP1 \cap HP2 \cap HP3 = \{ \, \} \, $ (himpunan kosong).
Jadi, penyelesaiannya adalah $ HP = \{ \, \} . \heartsuit $
Nomor 13
Jika $x$ dan $y$ memenuhi $2y^2-1>x$ dan $9y-x+4=0$ , maka $x-y$ memenuhi ...
$ 9y-x+4=0 \rightarrow x = 9y+4 \, \, $ ....pers(i)
$2y^2-1>x \, \, \, $ ....pert(ii)
$\spadesuit \, $ Substitusi pers(i) ke pert(ii)
$\begin{align} 2y^2-1 & > x \\ 2y^2-1 & > 9y+4 \\ 2y^2 -9y -5 & > 0 \\ (2y+1)(y-5) & > 0 \\ y = -\frac{1}{2} & \vee y = 5 \end{align}$

diperoleh : $ y < -\frac{1}{2} \vee y > 5 $
$\spadesuit \, $ Substitusi $ y < -\frac{1}{2} \vee y > 5 $
$ x = 9y + 4 \rightarrow x - y = 8y + 4 $
$ \begin{align} y < -\frac{1}{2} \rightarrow x - y & < 8 ( -\frac{1}{2} ) + 4 \\ & < -4 + 4 \\ & < 0 \\ y > 5 \rightarrow x - y & > 8 . 5 + 4 \\ & > 40 + 4 \\ & > 44 \end{align} $
Jadi, diperoleh $ x-y < 0 \vee x-y > 44 . \heartsuit $
$2y^2-1>x \, \, \, $ ....pert(ii)
$\spadesuit \, $ Substitusi pers(i) ke pert(ii)
$\begin{align} 2y^2-1 & > x \\ 2y^2-1 & > 9y+4 \\ 2y^2 -9y -5 & > 0 \\ (2y+1)(y-5) & > 0 \\ y = -\frac{1}{2} & \vee y = 5 \end{align}$

diperoleh : $ y < -\frac{1}{2} \vee y > 5 $
$\spadesuit \, $ Substitusi $ y < -\frac{1}{2} \vee y > 5 $
$ x = 9y + 4 \rightarrow x - y = 8y + 4 $
$ \begin{align} y < -\frac{1}{2} \rightarrow x - y & < 8 ( -\frac{1}{2} ) + 4 \\ & < -4 + 4 \\ & < 0 \\ y > 5 \rightarrow x - y & > 8 . 5 + 4 \\ & > 40 + 4 \\ & > 44 \end{align} $
Jadi, diperoleh $ x-y < 0 \vee x-y > 44 . \heartsuit $
Nomor 14
Diketahui untuk bilangan real positif $a,b,c,p,q,$ dan $r$ berlaku $\frac{a}{p}=\frac{b}{q}=\frac{c}{r}$.
Nilai dari $\frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)}$ adalah ...
$\spadesuit \, $ Permisalan: $ t = \frac{a}{p}=\frac{b}{q}=\frac{c}{r} $
Diperoleh : $ a = pt, \, b=qt, \, c = rt $
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} & \frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)} \\ & = \frac{pt.qt.rt(p+q)(q+r)(r+p)}{pqr(pt+qt)(qt+rt)(rt+pt)} \\ & = \frac{pqrt^3(p+q)(q+r)(r+p)}{pqr.t(p+q).t.(q+r).t.(r+p)} \\ & = \frac{pqrt^3(p+q)(q+r)(r+p)}{pqrt^3(p+q)(q+r)(r+p)} \\ & = 1 \end{align}$
Jadi, nilai $ \frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)} = 1 . \heartsuit $
Diperoleh : $ a = pt, \, b=qt, \, c = rt $
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} & \frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)} \\ & = \frac{pt.qt.rt(p+q)(q+r)(r+p)}{pqr(pt+qt)(qt+rt)(rt+pt)} \\ & = \frac{pqrt^3(p+q)(q+r)(r+p)}{pqr.t(p+q).t.(q+r).t.(r+p)} \\ & = \frac{pqrt^3(p+q)(q+r)(r+p)}{pqrt^3(p+q)(q+r)(r+p)} \\ & = 1 \end{align}$
Jadi, nilai $ \frac{abc(p+q)(q+r)(r+p)}{pqr(a+b)(b+c)(c+a)} = 1 . \heartsuit $
Nomor 15
Jika diketahui $x<0$ , maka banyaknya penyelesaian yang memenuhi sistem persamaan $\left\{ \begin{array}{c} x^2-ax+2014=0 \\ x^2-2014x+a=0 \end{array} \right.$ , adalah ...
$\clubsuit \, $ Kurangkan kedua persamaan
$\begin{array}{cc} x^2-ax+2014=0 & \\ x^2-2014x+a=0 & - \\ \hline (-a+2014)x+(-a+2014) = 0 & \end{array} $
Bentuk $ (-a+2014)x+(-a+2014) = 0 $ mempunyai penyelesaian hanya untuk $ x = -1 $
Cara : $ (-a+2014)x+(-a+2014) = 0 $
$ \rightarrow (-a+2014)x = - (-a+2014) $
$ \rightarrow x = \frac{- (-a+2014)}{(-a+2014)} = -1 $
Jadi, banyaknya penyelesaian ada satu solusi nilai $ x $ yaitu $ x = -1 . \heartsuit $
$\begin{array}{cc} x^2-ax+2014=0 & \\ x^2-2014x+a=0 & - \\ \hline (-a+2014)x+(-a+2014) = 0 & \end{array} $
Bentuk $ (-a+2014)x+(-a+2014) = 0 $ mempunyai penyelesaian hanya untuk $ x = -1 $
Cara : $ (-a+2014)x+(-a+2014) = 0 $
$ \rightarrow (-a+2014)x = - (-a+2014) $
$ \rightarrow x = \frac{- (-a+2014)}{(-a+2014)} = -1 $
Jadi, banyaknya penyelesaian ada satu solusi nilai $ x $ yaitu $ x = -1 . \heartsuit $
Jika ada masukan, saran, kritikan, alternatif penyelesaian lain yang lebih mudah, atau apapun yang berhubungan dengan halaman ini, silahkan kirim ke email : d.4rm.408@gmail.com , atau langsung isi komentar pada kotak komentar di bawah ini. Semoga bermanfaat, terima kasih.