Nomor 11
Diketahui $ \, f(x) = -2x^2 -(p+1)x + 2p. \, $ Fungsi $ f(x) \, $ mempunyai nilai maksimum 8. Jika $ p \, $ bernilai $ p_1 \, $
atau $ p_2 . \, $ Nilai $ p_1 + p_2 \, $ adalah ....
$\spadesuit \, $ FK : $ f(x) = -2x^2 -(p+1)x + 2p $
$ \rightarrow a = -2, b = -(p+1), c = 2p $
$\spadesuit \, $ Nilai maksimum FK ($y_p$) dengan rumus $ y_p = \frac{D}{-4a} $
$\spadesuit \, $ Menentukan nilai $ p \, $ dengan $ \, y_p = 8 $
$\begin{align} y_p & = 8 \\ \frac{D}{-4a} & = 8 \\ \frac{b^2 - 4ac}{-4a} & = 8 \\ \frac{[-(p+1)]^2 - 4.(-2).(2p)}{-4.(-2)} & = 8 \\ \frac{ p^2 + 2p + 1 + 16p }{8} & = 8 \\ p^2 + 18p + 1 & = 64 \\ p^2 + 18p - 63 & = 0 \end{align}$
PK : $ p^2 + 18p - 63 = 0 , \, $ akar-akarnya $ p_1 \, $ dan $ \, p_2 $
Sehingga : $ p_1 + p_2 = \frac{-b}{a} = \frac{-18}{1} = -18 $
Jadi, nilai $ p_1 + p_2 = - 18 . \heartsuit $
$ \rightarrow a = -2, b = -(p+1), c = 2p $
$\spadesuit \, $ Nilai maksimum FK ($y_p$) dengan rumus $ y_p = \frac{D}{-4a} $
$\spadesuit \, $ Menentukan nilai $ p \, $ dengan $ \, y_p = 8 $
$\begin{align} y_p & = 8 \\ \frac{D}{-4a} & = 8 \\ \frac{b^2 - 4ac}{-4a} & = 8 \\ \frac{[-(p+1)]^2 - 4.(-2).(2p)}{-4.(-2)} & = 8 \\ \frac{ p^2 + 2p + 1 + 16p }{8} & = 8 \\ p^2 + 18p + 1 & = 64 \\ p^2 + 18p - 63 & = 0 \end{align}$
PK : $ p^2 + 18p - 63 = 0 , \, $ akar-akarnya $ p_1 \, $ dan $ \, p_2 $
Sehingga : $ p_1 + p_2 = \frac{-b}{a} = \frac{-18}{1} = -18 $
Jadi, nilai $ p_1 + p_2 = - 18 . \heartsuit $
Nomor 12
Integral yang menyatakan luas daerah di kuadran pertama yang dibatasi oleh kurva $ \, y = \frac{1}{x} \, $ , garis $ \, y = x, \, $
garis $ \, x = 2, \, $ dan sumbu X adalah ....
$\clubsuit \, $ Gambar

$\clubsuit \, $ Menentukan luas arsir
$\begin{align} L_{arsir} & = L_A + L_B \\ L_{arsir} & = \int \limits_0^1 x \, dx + \int \limits_1^2 \frac{1}{x} \, dx \end{align}$
Jadi, luasnya adalah $ \int \limits_0^1 x \, dx + \int \limits_1^2 \frac{1}{x} \, dx . \heartsuit $

$\clubsuit \, $ Menentukan luas arsir
$\begin{align} L_{arsir} & = L_A + L_B \\ L_{arsir} & = \int \limits_0^1 x \, dx + \int \limits_1^2 \frac{1}{x} \, dx \end{align}$
Jadi, luasnya adalah $ \int \limits_0^1 x \, dx + \int \limits_1^2 \frac{1}{x} \, dx . \heartsuit $
Nomor 13
Satu dari dua persamaan garis singgung dari lingkaran $ x^2 + y^2 - 2x - 4y = 0 \, $ yang tegak lurus terhadap garis
$ x - 2y + 4 = 0 \, $ adalah ....
$\spadesuit \, $ Menentukan pusat dan jari-jari lingkaran
$ x^2 + y^2 - 2x - 4y = 0 \rightarrow A = -2, B = -4, C = 0 $
Pusat ($a,b$) dengan $ a = - \frac{A}{2} = - \frac{-2}{2} = 1 \, $ dan $ \, b = -\frac{B}{2} = -\frac{-4}{2} = 2 $
Sehingga pusatnya : $ (a,b) = (1,2) $
jari-jari : $ r =\sqrt{a^2+b^2-C} = \sqrt{1^2+2^2-0} = \sqrt{5} $
$\spadesuit \, $ Menentukan gradien garis singgungnya
$ x - 2y + 4 = 0 \rightarrow m_1 = \frac{-x}{y} = \frac{-1}{-2} = \frac{1}{2} $
Garis singgung tegak lurus, maka gradiennya :
$m.m_1 = -1 \rightarrow m = \frac{-1}{m_1} = \frac{-1}{\frac{1}{2}} = -2 $
$\spadesuit \, $ Menentukan persamaan garis singgung lingkaran
$\begin{align} y-b & = m(x-a) \pm r \sqrt{1+m^2} \\ y-2 & = -2(x-1) \pm \sqrt{5} \sqrt{1+(-2)^2} \\ y-2 & = -2x + 1 \pm \sqrt{5} \sqrt{5} \\ y-2 & = -2x + 1 \pm 5 \\ (i). \, y-2 & = -2x + 1 + 5 \rightarrow y+2x - 9 = 0 \\ & \text{(atau)} \\ (ii). \, y-2 & = -2x + 1 - 5 \rightarrow y+2x + 1 = 0 \end{align}$
Jadi, persamaan garis singgungnya adalah
$ y+2x - 9 = 0 \vee y+2x + 1 = 0. \heartsuit $
$ x^2 + y^2 - 2x - 4y = 0 \rightarrow A = -2, B = -4, C = 0 $
Pusat ($a,b$) dengan $ a = - \frac{A}{2} = - \frac{-2}{2} = 1 \, $ dan $ \, b = -\frac{B}{2} = -\frac{-4}{2} = 2 $
Sehingga pusatnya : $ (a,b) = (1,2) $
jari-jari : $ r =\sqrt{a^2+b^2-C} = \sqrt{1^2+2^2-0} = \sqrt{5} $
$\spadesuit \, $ Menentukan gradien garis singgungnya
$ x - 2y + 4 = 0 \rightarrow m_1 = \frac{-x}{y} = \frac{-1}{-2} = \frac{1}{2} $
Garis singgung tegak lurus, maka gradiennya :
$m.m_1 = -1 \rightarrow m = \frac{-1}{m_1} = \frac{-1}{\frac{1}{2}} = -2 $
$\spadesuit \, $ Menentukan persamaan garis singgung lingkaran
$\begin{align} y-b & = m(x-a) \pm r \sqrt{1+m^2} \\ y-2 & = -2(x-1) \pm \sqrt{5} \sqrt{1+(-2)^2} \\ y-2 & = -2x + 1 \pm \sqrt{5} \sqrt{5} \\ y-2 & = -2x + 1 \pm 5 \\ (i). \, y-2 & = -2x + 1 + 5 \rightarrow y+2x - 9 = 0 \\ & \text{(atau)} \\ (ii). \, y-2 & = -2x + 1 - 5 \rightarrow y+2x + 1 = 0 \end{align}$
Jadi, persamaan garis singgungnya adalah
$ y+2x - 9 = 0 \vee y+2x + 1 = 0. \heartsuit $
Nomor 14
Rata-rata nilai ujian matematika dari 30 siswa adalah 88. Jika rata-rata nilai ujian itu untuk semua anak laki-laki
dan semua anak perempuan berturut-turut adalah 85 dan 90, maka banyaknya anak laki-laki adalah ....
$\clubsuit \,$ Misal :
$ \overline{x}_{gb} = 88 \rightarrow \, $ rata - rata gabungan
$ \overline{x}_{p} = 90 \rightarrow \, $ rata - rata perempuan
$ \overline{x}_{l} = 85 \rightarrow \, $ rata - rata laki - laki
Misal, banyak anak laki $n_l $ , maka banyak anak perempuan $ n_p = 30 - n_l $
$\clubsuit \,$ Menentukan $ n_l $ dengan rata - rata gabungan
$\begin{align} \overline{x}_{gb} & = \frac{n_p.\overline{x}_p + n_l . \overline{x}_l}{n_p + n_l} \\ 88 & = \frac{(30-n_l).90 + n_l . 85}{(30-n_l) + n_l} \\ 88 & = \frac{(30-n_l).90 + 85n_l}{30} \\ 88. 30 & = 30.90 - n_l . 90 + 85n_l \\ 88. 30 & = 30.90 - 5 n_l \\ 5n_l & = 30.90 - 88. 30 \\ 5n_l & = 30 . 2 \\ n_l & = \frac{30. 2}{5} = 12 \end{align} $
Jadi, banyaknya anak laki - laki ada 12 siswa. $ \heartsuit $
$ \overline{x}_{gb} = 88 \rightarrow \, $ rata - rata gabungan
$ \overline{x}_{p} = 90 \rightarrow \, $ rata - rata perempuan
$ \overline{x}_{l} = 85 \rightarrow \, $ rata - rata laki - laki
Misal, banyak anak laki $n_l $ , maka banyak anak perempuan $ n_p = 30 - n_l $
$\clubsuit \,$ Menentukan $ n_l $ dengan rata - rata gabungan
$\begin{align} \overline{x}_{gb} & = \frac{n_p.\overline{x}_p + n_l . \overline{x}_l}{n_p + n_l} \\ 88 & = \frac{(30-n_l).90 + n_l . 85}{(30-n_l) + n_l} \\ 88 & = \frac{(30-n_l).90 + 85n_l}{30} \\ 88. 30 & = 30.90 - n_l . 90 + 85n_l \\ 88. 30 & = 30.90 - 5 n_l \\ 5n_l & = 30.90 - 88. 30 \\ 5n_l & = 30 . 2 \\ n_l & = \frac{30. 2}{5} = 12 \end{align} $
Jadi, banyaknya anak laki - laki ada 12 siswa. $ \heartsuit $
Nomor 15
Diketahui sebelas orang duduk mengelilingi meja. Jika tiga orang tertentu harus duduk berdampingan, banyak cara kesebelas
orang tersebut dapat duduk adalah ....
$\clubsuit \,$ Gambar
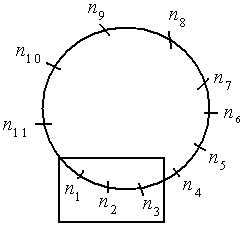
$\clubsuit \,$ Agar 3 orang selalu bersama, kita blok tiga orang tersebut (seperti gambar) dan dianggap menjadi satu orang , sehingga sekarang toal ada 9 orang duduk melingkar dengan cara duduk = (9 - 1)! = 8!
$\clubsuit \,$ Dari tiga orang yang diblok tadi ada 3! susunan
sehingga total cara = 3!.8!
Jadi, total cara duduk ada 3!.8! susunan. $ \heartsuit $

$\clubsuit \,$ Agar 3 orang selalu bersama, kita blok tiga orang tersebut (seperti gambar) dan dianggap menjadi satu orang , sehingga sekarang toal ada 9 orang duduk melingkar dengan cara duduk = (9 - 1)! = 8!
$\clubsuit \,$ Dari tiga orang yang diblok tadi ada 3! susunan
sehingga total cara = 3!.8!
Jadi, total cara duduk ada 3!.8! susunan. $ \heartsuit $