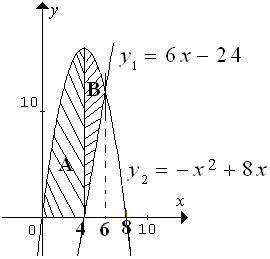
Nomor 11
Diberikan kurva $y=x^3+2x^2-x+5$ . Jika garis singgung kurva di titik ($a,b$) sejajar dengan garis $y-3x-4=0$ , maka nilai
$b$ yang mungkin adalah ...
$\clubsuit \, $ Garis $y-3x-4=0$ memiliki gradien $m=\frac{-x}{y} = \frac{-(-3)}{1} = 3 $
$\clubsuit \, $ Gradien garis singgung sejajar dengan garis $y-3x-4=0$ artinya gradiennya sama yaitu $m = 3 $
$\clubsuit \, $ Gradien garis singgung di titik ($a,b$) : $m = f^\prime (a) $
$\begin{align*} y & = x^3+2x^2-x+5 \\ y^\prime & = 3x^2+4x-1 \\ m & = f^\prime (a) \\ 3 & = 3a^2+4a-1 \\ 3a^2+4a -4 & = 0 \\ (3a-2)(a+2) & = 0 \\ a=\frac{3}{2} & \vee a = -2 \end{align*}$
$\clubsuit \, $ Substitusi $a=-2$ ke kurva
$\begin{align*} a=-2 \rightarrow y & = x^3+2x^2-x+5 \\ b & = (-2)^3+2(-2)^2-(-2)+5 \\ b & = -8+8+2+5 \\ b & = 7 \end{align*}$
Jadi, salah satu nilai $b$ yang mungkin adalah 7 . $\heartsuit $
$\clubsuit \, $ Gradien garis singgung sejajar dengan garis $y-3x-4=0$ artinya gradiennya sama yaitu $m = 3 $
$\clubsuit \, $ Gradien garis singgung di titik ($a,b$) : $m = f^\prime (a) $
$\begin{align*} y & = x^3+2x^2-x+5 \\ y^\prime & = 3x^2+4x-1 \\ m & = f^\prime (a) \\ 3 & = 3a^2+4a-1 \\ 3a^2+4a -4 & = 0 \\ (3a-2)(a+2) & = 0 \\ a=\frac{3}{2} & \vee a = -2 \end{align*}$
$\clubsuit \, $ Substitusi $a=-2$ ke kurva
$\begin{align*} a=-2 \rightarrow y & = x^3+2x^2-x+5 \\ b & = (-2)^3+2(-2)^2-(-2)+5 \\ b & = -8+8+2+5 \\ b & = 7 \end{align*}$
Jadi, salah satu nilai $b$ yang mungkin adalah 7 . $\heartsuit $
Nomor 12
Grafik $y=f^\prime (x) $ ditunjukkan pada gambar berikut

Pernyataan yang benar adalah ...

Pernyataan yang benar adalah ...
$\spadesuit \, $ Titik maksimum/minimum saat $f^\prime (x) = 0 $
Dari gambar di atas, $f^\prime (x) = 0 $ tercapai untuk $x=-2$ dan $x=2$ , artinya titik maksimum/minimum saat $x=-2$ dan $x=2$ .
$\spadesuit \, $ Fungsi naik/turun
fungsi turun dengan syarat $f^\prime (x) < 0 $ ($ f^\prime (x) $ negatif)
fungsi naik dengan syarat $f^\prime (x) > 0 $ ($ f^\prime (x) $ positif)
Dari gambar di atas :
* $f^\prime (x) $ negatif (bagian kurva di bawah sumbu X) ada pada interval $-2 < x < 2 $ , artinya $y=f(x) $ turun pada interval $-2 < x < 2 $
* $f^\prime (x) $ positif (bagian kurva di atas sumbu X) ada pada interval $ x < -2 \vee x > 2 $ , artinya $y=f(x) $ naik pada interval $ x < -2 \vee x > 2 $
$\spadesuit \, $ Deskripsi gambar fungsi awal $y=f(x) $


Jadi, fungsi $y=f(x) $ minimum saat $x = 2 . \heartsuit $
Dari gambar di atas, $f^\prime (x) = 0 $ tercapai untuk $x=-2$ dan $x=2$ , artinya titik maksimum/minimum saat $x=-2$ dan $x=2$ .
$\spadesuit \, $ Fungsi naik/turun
fungsi turun dengan syarat $f^\prime (x) < 0 $ ($ f^\prime (x) $ negatif)
fungsi naik dengan syarat $f^\prime (x) > 0 $ ($ f^\prime (x) $ positif)
Dari gambar di atas :
* $f^\prime (x) $ negatif (bagian kurva di bawah sumbu X) ada pada interval $-2 < x < 2 $ , artinya $y=f(x) $ turun pada interval $-2 < x < 2 $
* $f^\prime (x) $ positif (bagian kurva di atas sumbu X) ada pada interval $ x < -2 \vee x > 2 $ , artinya $y=f(x) $ naik pada interval $ x < -2 \vee x > 2 $
$\spadesuit \, $ Deskripsi gambar fungsi awal $y=f(x) $


Jadi, fungsi $y=f(x) $ minimum saat $x = 2 . \heartsuit $
Nomor 13
Diketahui vektor $\vec{u} = (1, -3a+1, 2) $ dan $\vec{v} = (a^3-3a^2, 3, 0) $ dengan $-2 < a < 4 $ . Nilai maksimum
$\vec{u} . \vec{v} $ adalah ...
$\spadesuit \, $ Menentukan $\vec{u}.\vec{v} $
$\begin{align*} \vec{u}.\vec{v} & = 1.(a^3-3a^2) + (-3a+1).3 + 2.0 \\ f(a) & = a^3-3a^2-9a+3 \\ f^\prime (a) & = 3a^2 - 6a - 9 \end{align*}$
$\spadesuit \, $ Menentukan nilai maksimum
$\begin{align*} f^\prime (a) & = 0 \\ 3a^2 - 6a - 9 & = 0 \, \, \, \text{(bagi 3)} \\ a^2 - 2a - 3 & = 0 \\ (a+1)(a-3) & = 0 \\ a=-1 & \vee a = 3 \end{align*}$
$\spadesuit \, $ Substitusi semua nilai $a$ ke fungsi awal
$a=-1 \rightarrow f(-1)= (-1)^3-3.(-1)^2-9.(-1)+3 = 8 $
$a=3 \rightarrow f(3)= (3)^3-3.(3)^2-9.(3)+3 = -24 $
Jadi, nilai maksimumnya adalah 8. $ \heartsuit $
$\begin{align*} \vec{u}.\vec{v} & = 1.(a^3-3a^2) + (-3a+1).3 + 2.0 \\ f(a) & = a^3-3a^2-9a+3 \\ f^\prime (a) & = 3a^2 - 6a - 9 \end{align*}$
$\spadesuit \, $ Menentukan nilai maksimum
$\begin{align*} f^\prime (a) & = 0 \\ 3a^2 - 6a - 9 & = 0 \, \, \, \text{(bagi 3)} \\ a^2 - 2a - 3 & = 0 \\ (a+1)(a-3) & = 0 \\ a=-1 & \vee a = 3 \end{align*}$
$\spadesuit \, $ Substitusi semua nilai $a$ ke fungsi awal
$a=-1 \rightarrow f(-1)= (-1)^3-3.(-1)^2-9.(-1)+3 = 8 $
$a=3 \rightarrow f(3)= (3)^3-3.(3)^2-9.(3)+3 = -24 $
Jadi, nilai maksimumnya adalah 8. $ \heartsuit $
Nomor 14
Bola dengan diameter 8 cm seluruhnya terdapat dalam kerucut tegak terbalik. Tinggi kerucut dengan volume terkecil
yang mungkin adalah ... cm.
$\spadesuit \, $ Gambarnya
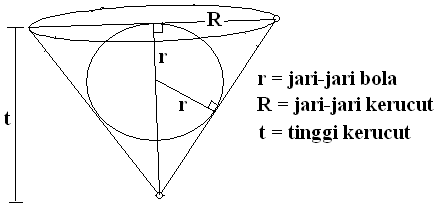
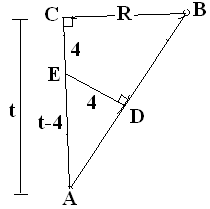
$AB = \sqrt{R^2+t^2} $
$\spadesuit \, $ Konsep kesebangunan pada $\Delta$AED dan $\Delta$ABC
$\begin{align*} \frac{ED}{BC} & = \frac{AE}{AB} \\ \frac{4}{R} & = \frac{t-4}{\sqrt{R^2+t^2}} \, \, \, \text{(kuadratkan)} \\ \frac{16}{R^2} & = \frac{t^2-8t+16}{R^2+t^2} \\ 16R^2+16t^2 & = R^2(t-8t)+16R^2 \\ R^2 & = \frac{16t^2}{t-8t} \\ R^2 & = \frac{16t}{t-8} \, \, \, \text{...pers(i)} \end{align*}$
$\spadesuit \, $ Volume maksimum/minimum, syarat : $V^\prime = 0 $
$\begin{align*} V & = \frac{1}{3} \pi R^2 t \, \, \, \text{substitusi pers(i)} \\ V & = \frac{1}{3} \pi .\frac{16t}{t-8} . t \\ V & = \frac{1}{3} \pi .\frac{16t^2}{t-8} \\ V^\prime & = 0 \\ \frac{16\pi}{3} \left[ \frac{2t(t-8)-t^2}{(t-8)^2} \right] & = 0 \\ \frac{16\pi}{3} \left[ \frac{t^2-16t}{(t-8)^2} \right] & = 0 \\ t^2-16t & = 0 \\ t(t-16) & = 0 \\ t=0 & \vee t=16 \end{align*}$
Jadi, tinggi kerucut adalah 16 cm. $ \heartsuit $


$AB = \sqrt{R^2+t^2} $
$\spadesuit \, $ Konsep kesebangunan pada $\Delta$AED dan $\Delta$ABC
$\begin{align*} \frac{ED}{BC} & = \frac{AE}{AB} \\ \frac{4}{R} & = \frac{t-4}{\sqrt{R^2+t^2}} \, \, \, \text{(kuadratkan)} \\ \frac{16}{R^2} & = \frac{t^2-8t+16}{R^2+t^2} \\ 16R^2+16t^2 & = R^2(t-8t)+16R^2 \\ R^2 & = \frac{16t^2}{t-8t} \\ R^2 & = \frac{16t}{t-8} \, \, \, \text{...pers(i)} \end{align*}$
$\spadesuit \, $ Volume maksimum/minimum, syarat : $V^\prime = 0 $
$\begin{align*} V & = \frac{1}{3} \pi R^2 t \, \, \, \text{substitusi pers(i)} \\ V & = \frac{1}{3} \pi .\frac{16t}{t-8} . t \\ V & = \frac{1}{3} \pi .\frac{16t^2}{t-8} \\ V^\prime & = 0 \\ \frac{16\pi}{3} \left[ \frac{2t(t-8)-t^2}{(t-8)^2} \right] & = 0 \\ \frac{16\pi}{3} \left[ \frac{t^2-16t}{(t-8)^2} \right] & = 0 \\ t^2-16t & = 0 \\ t(t-16) & = 0 \\ t=0 & \vee t=16 \end{align*}$
Jadi, tinggi kerucut adalah 16 cm. $ \heartsuit $
Cara II
$\spadesuit \, $ Gambarnya

$\spadesuit \, $ Berdasarkan gambar, volume kerucut minimum saat :
$t=4r \, \, $ dan $\, \, R = 2\sqrt{2}$
Sehingga $t=4r=4\times 4 = 16 $
Jadi, tinggi kerucut adalah 16 cm. $ \heartsuit $
$\spadesuit \, $ Gambarnya

$\spadesuit \, $ Berdasarkan gambar, volume kerucut minimum saat :
$t=4r \, \, $ dan $\, \, R = 2\sqrt{2}$
Sehingga $t=4r=4\times 4 = 16 $
Jadi, tinggi kerucut adalah 16 cm. $ \heartsuit $
Nomor 15
Diberikan lingkaran dengan persamaan $(x+5)^2+(y-12)^2= 14^2 $ . Jarak minimal titik pada lingkaran tersebut ke titik
asal adalah ...
$\clubsuit \, $ Unsur-unsur lingkaran
$(x-a)^2+(y-b)^2= r^2 \, \, \, \, $ memiliki pusat ($a,b$) dan jari-jari $r$
$(x+5)^2+(y-12)^2= 14^2 \, \, \, \, $ memiliki pusat (-5,12) dan $r=14$
$\clubsuit \, $ Gambarnya
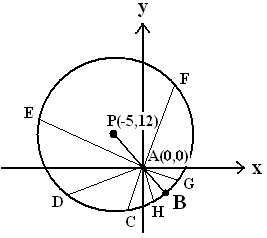
$\clubsuit \, $ Menentukan jarak PA
jarak titik P(-5,12) ke A(0,0)
$PA = \sqrt{((-5)-0)^2 + (12-0)^2 } = \sqrt{(-5)^2 + (12)^2 } = \sqrt{25 + 144 } = 13 $
$\clubsuit \, $ Menentukan jarak terdekat
Jarak terdekat/minimal titik pada lingkaran dengan titik asal (titik A(0,0)) yaitu jarak titik A ke semua titik yang ada pada lingkaran, misalkan AB, AC, AD, ... dan AH. Namun yang paling kecil jaraknya adalah AB. Sehingga jarak minimalnya adalah AB, dengan PB sama dengan jari-jari lingkaran.
$\begin{align*} AB & = PB - PA \\ & = r - PA \\ & = 14 - 13 \\ AB & = 1 \end{align*}$
Jadi, jarak minimalnya adalah 1. $ \heartsuit $
$(x-a)^2+(y-b)^2= r^2 \, \, \, \, $ memiliki pusat ($a,b$) dan jari-jari $r$
$(x+5)^2+(y-12)^2= 14^2 \, \, \, \, $ memiliki pusat (-5,12) dan $r=14$
$\clubsuit \, $ Gambarnya

$\clubsuit \, $ Menentukan jarak PA
jarak titik P(-5,12) ke A(0,0)
$PA = \sqrt{((-5)-0)^2 + (12-0)^2 } = \sqrt{(-5)^2 + (12)^2 } = \sqrt{25 + 144 } = 13 $
$\clubsuit \, $ Menentukan jarak terdekat
Jarak terdekat/minimal titik pada lingkaran dengan titik asal (titik A(0,0)) yaitu jarak titik A ke semua titik yang ada pada lingkaran, misalkan AB, AC, AD, ... dan AH. Namun yang paling kecil jaraknya adalah AB. Sehingga jarak minimalnya adalah AB, dengan PB sama dengan jari-jari lingkaran.
$\begin{align*} AB & = PB - PA \\ & = r - PA \\ & = 14 - 13 \\ AB & = 1 \end{align*}$
Jadi, jarak minimalnya adalah 1. $ \heartsuit $