Nomor 11
$\int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx = ...$
Substitusi $U=3x^2 + 1 \Rightarrow U^\prime = 6x $
$\int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx = \int 3x \left( 3x^2 + 1 \right)^{-2} dx $
$\begin{align*} \int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx &= \int 3x \left( 3x^2 + 1 \right) ^{-2} dx \\ &= \int 3x \left( U \right) ^{-2} \frac{dU}{U^\prime} \\ &=\int 3x \left( U \right) ^{-2} \frac{dU}{6x} \\ &=\frac{1}{2} \int U^{-2} dU \\ &=\frac{1}{2} . \frac{1}{-1} U^{-1} + c \\ &=- \frac{1}{2} \frac{1}{U} + c \\ &=- \frac{1}{2} \frac{1}{\left( 3x^2 + 1 \right)} + c \\ &=- \frac{1}{2\left( 3x^2 + 1 \right)} + c \, \heartsuit \end{align*}$
$\int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx = \int 3x \left( 3x^2 + 1 \right)^{-2} dx $
$\begin{align*} \int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx &= \int 3x \left( 3x^2 + 1 \right) ^{-2} dx \\ &= \int 3x \left( U \right) ^{-2} \frac{dU}{U^\prime} \\ &=\int 3x \left( U \right) ^{-2} \frac{dU}{6x} \\ &=\frac{1}{2} \int U^{-2} dU \\ &=\frac{1}{2} . \frac{1}{-1} U^{-1} + c \\ &=- \frac{1}{2} \frac{1}{U} + c \\ &=- \frac{1}{2} \frac{1}{\left( 3x^2 + 1 \right)} + c \\ &=- \frac{1}{2\left( 3x^2 + 1 \right)} + c \, \heartsuit \end{align*}$
Nomor 12
Jika ${}^{b} log a + {}^{a} log b^4 = 5$ , maka nilai ${}^{b} log a$ yang mungkin adalah ...
Sifat logaritma : ${}^{a} log b = \frac{1}{{}^{b} log a} \, $ dan $\, {}^{a} log b^n = n {}^{a} log b $
Misal : $ p = {}^{b} log a $
$\begin{align*} {}^{b} log a + {}^{a} log b^4 &= 5 \\ {}^{b} log a + 4 {}^{a} log b &= 5 \\ {}^{b} log a + 4 \frac{1}{{}^{b} log a} &= 5 \, \, \, \left( p = {}^{b} log a \right) \\ p + \frac{4}{p} &= 5 \, \, \, (\text{kali} \, p) \\ p^2 + 4 &= 5p \\ p^2 - 5p +4 &= 0 \\ (p-1)(p-4)&=0 \\ p=1 \, \text{atau} \, p=4 \end{align*}$
Jadi, nilai $ {}^{b} log a \, $ adalah 1 atau 4 . $\heartsuit $
Misal : $ p = {}^{b} log a $
$\begin{align*} {}^{b} log a + {}^{a} log b^4 &= 5 \\ {}^{b} log a + 4 {}^{a} log b &= 5 \\ {}^{b} log a + 4 \frac{1}{{}^{b} log a} &= 5 \, \, \, \left( p = {}^{b} log a \right) \\ p + \frac{4}{p} &= 5 \, \, \, (\text{kali} \, p) \\ p^2 + 4 &= 5p \\ p^2 - 5p +4 &= 0 \\ (p-1)(p-4)&=0 \\ p=1 \, \text{atau} \, p=4 \end{align*}$
Jadi, nilai $ {}^{b} log a \, $ adalah 1 atau 4 . $\heartsuit $
Nomor 13
Jika $y + 3z = 11$ , $x + y = 3$ , dan $2x + 5z = 17$ maka $3x + 2y + z = ...$
$ \text{SPL} : \left\{ \begin{array}{ll}
y + 3z = 11 \Rightarrow y=11-3z & \text{....(persmaan (i))}\\
x + y = 3 & \mbox{...(persmaan (ii))} \\
2x + 5z = 17 & \mbox{...(persmaan (iii))}
\end{array} \right. $
$\clubsuit \,$ Substitusi pers (i) ke pers (ii):
$x+y=3 \Leftrightarrow x+(11-3z)=3 \Leftrightarrow x=3z-8 \, \text{....persamaan (iv)}$
$\clubsuit \,$ Substitusi pers (iv) ke pers (iii):
$2x + 5z = 17 \Leftrightarrow 2(3z-8) +5z=17 \Leftrightarrow z=3$
$\clubsuit \, x=3z-8 \Leftrightarrow x=3.3-8 \Leftrightarrow x=1$
$\clubsuit \, x + y = 3 \Leftrightarrow 1 + y = 3 \Leftrightarrow y=2 $
Sehingga : $3x + 2y + z = 3.1 + 2.2 + 3 = 10 \, \heartsuit $
$\clubsuit \,$ Substitusi pers (i) ke pers (ii):
$x+y=3 \Leftrightarrow x+(11-3z)=3 \Leftrightarrow x=3z-8 \, \text{....persamaan (iv)}$
$\clubsuit \,$ Substitusi pers (iv) ke pers (iii):
$2x + 5z = 17 \Leftrightarrow 2(3z-8) +5z=17 \Leftrightarrow z=3$
$\clubsuit \, x=3z-8 \Leftrightarrow x=3.3-8 \Leftrightarrow x=1$
$\clubsuit \, x + y = 3 \Leftrightarrow 1 + y = 3 \Leftrightarrow y=2 $
Sehingga : $3x + 2y + z = 3.1 + 2.2 + 3 = 10 \, \heartsuit $
Nomor 14
Nilai $\displaystyle\lim_{x \to 3} \frac{6\left( \sqrt{x} - \sqrt{3} \right) }{x^2 - 3x}$ adalah ...
$\spadesuit \, $ Merasionalkan pembilang :
$\begin{align*} \displaystyle\lim_{x \to 3} \frac{6\left( \sqrt{x} - \sqrt{3} \right) }{x^2 - 3x} \frac{ \sqrt{x} + \sqrt{3}}{\sqrt{x} + \sqrt{3}} &= \displaystyle\lim_{x \to 3} \frac{6\left( x-3 \right) }{x(x-3)\left( \sqrt{x} + \sqrt{3} \right)} \\ &= \displaystyle\lim_{x \to 3} \frac{6}{x\left( \sqrt{x} + \sqrt{3} \right)} \\ &= \frac{6}{3\left( \sqrt{3} + \sqrt{3} \right)}\\ &= \frac{6}{3\left( 2 \sqrt{3} \right)}\\ &= \frac{1}{\left( \sqrt{3} \right)}\\ &= \frac{1}{3} \sqrt{3} \, \heartsuit \end{align*}$
$\begin{align*} \displaystyle\lim_{x \to 3} \frac{6\left( \sqrt{x} - \sqrt{3} \right) }{x^2 - 3x} \frac{ \sqrt{x} + \sqrt{3}}{\sqrt{x} + \sqrt{3}} &= \displaystyle\lim_{x \to 3} \frac{6\left( x-3 \right) }{x(x-3)\left( \sqrt{x} + \sqrt{3} \right)} \\ &= \displaystyle\lim_{x \to 3} \frac{6}{x\left( \sqrt{x} + \sqrt{3} \right)} \\ &= \frac{6}{3\left( \sqrt{3} + \sqrt{3} \right)}\\ &= \frac{6}{3\left( 2 \sqrt{3} \right)}\\ &= \frac{1}{\left( \sqrt{3} \right)}\\ &= \frac{1}{3} \sqrt{3} \, \heartsuit \end{align*}$
Nomor 15
Daerah $D$ dibatasi oleh grafik $y = x^2$ dan $y = 2x^2 - 1$. Luas daerah $D$ dapat dinyatakan sebagai ...
Titik potong kedua kurva:
$\begin{align*} y_1 &= y_2 \\ 2x^2 - 1 &= x^2 \\ x^2 - 1 &= 0 \\ x&= \pm 1 \end{align*}$
Grafik kedua fungsi :
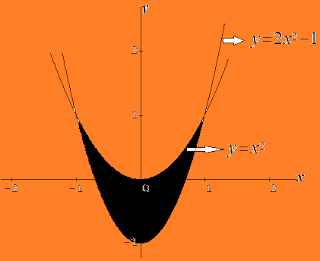
Menghitung luas daerah yang diarsir:
$\begin{align*} L_\text{arsir} &= \int_{-1}^{1} \text{(kurva atas)} - \text{(kurva bawah)} dx \\ &= \int_{-1}^{1} (x^2) - (2x^2 - 1) dx \\ &= \int_{-1}^{1} (-x^2 + 1) dx \end{align*}$
Jadi luasnya : $ \int_{-1}^{1} (-x^2 + 1) dx . \heartsuit $
$\begin{align*} y_1 &= y_2 \\ 2x^2 - 1 &= x^2 \\ x^2 - 1 &= 0 \\ x&= \pm 1 \end{align*}$
Grafik kedua fungsi :

Menghitung luas daerah yang diarsir:
$\begin{align*} L_\text{arsir} &= \int_{-1}^{1} \text{(kurva atas)} - \text{(kurva bawah)} dx \\ &= \int_{-1}^{1} (x^2) - (2x^2 - 1) dx \\ &= \int_{-1}^{1} (-x^2 + 1) dx \end{align*}$
Jadi luasnya : $ \int_{-1}^{1} (-x^2 + 1) dx . \heartsuit $






%2BIndonesia.jpeg)