Nomor 11
Misalkan $ l_1 \, $ dan $ l_2 \, $ menyatakan garis yang menyinggung lingkaran $ x^2 + y^2 = r^2 \, $ berturut-turut di
$ P_1(x_1,y_1) \, $ dan $ P_2(x_2,y_2) \, $ . Jika $ l_1 \, $ dan $ l_2 \, $ berpotongan di $ (2,-1) \, $ dan titik $ (4,-1) \, $
berada pada garis yang melalui $ P_1 \, $ dan $ P_2 \, $ , maka $ r = ..... $
$\clubsuit \, $ Gambar
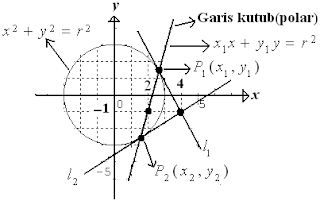
Dari gambar di atas, garis yang menghubungkan titik $ P_1 \, $ dan $ P_2 \, $ disebut garis kutub(polar) dengan persamaan $ x_1x+y_1y = r^2 \, $ yang dibentuk dari kedua garis singgung lingkaran $ l_1 \, $ dan $ l_2 \, $ yang berpotongan di titik (4,-1).
Persamaan garis kutub dari titik (4,-1) adalah
$ x_1x+y_1y = r^2 \rightarrow 4x - y = r^2 $
$\clubsuit \, $ Menentukan nilai $ r \, $ dengan substitusi titik (2,-1) ke persamaan garis kutub (garis kutub melalui titik (2,-1) ).
$\begin{align} (x,y)=(2,-1) \rightarrow 4x - y & = r^2 \\ 4.2 - (-1) & = r^2 \\ 8 + 1 & = r^2 \\ 9 & = r^2 \\ r & = 3 \end{align}$
Jadi, nilai $ r = 3 . \heartsuit $
Catatan : Dari soal, sebenarnya kedua garis singgung berpotongan di titik (2,-1) , akan tetapi itu tidak mungkin karena gambar lingkarannya akan semakin kecil sehingga garis kutubnya tidak mungkin melalui titik (4,-1). Maka dari itu, kasusnya di balik yaituu kedua garis singgung berpotongan di titik (4,-1) dan garis kutub melalui titik (2,-1) seperti gambar di atas. Ini artinya ada kesalahan pengetikan pada soal.

Dari gambar di atas, garis yang menghubungkan titik $ P_1 \, $ dan $ P_2 \, $ disebut garis kutub(polar) dengan persamaan $ x_1x+y_1y = r^2 \, $ yang dibentuk dari kedua garis singgung lingkaran $ l_1 \, $ dan $ l_2 \, $ yang berpotongan di titik (4,-1).
Persamaan garis kutub dari titik (4,-1) adalah
$ x_1x+y_1y = r^2 \rightarrow 4x - y = r^2 $
$\clubsuit \, $ Menentukan nilai $ r \, $ dengan substitusi titik (2,-1) ke persamaan garis kutub (garis kutub melalui titik (2,-1) ).
$\begin{align} (x,y)=(2,-1) \rightarrow 4x - y & = r^2 \\ 4.2 - (-1) & = r^2 \\ 8 + 1 & = r^2 \\ 9 & = r^2 \\ r & = 3 \end{align}$
Jadi, nilai $ r = 3 . \heartsuit $
Catatan : Dari soal, sebenarnya kedua garis singgung berpotongan di titik (2,-1) , akan tetapi itu tidak mungkin karena gambar lingkarannya akan semakin kecil sehingga garis kutubnya tidak mungkin melalui titik (4,-1). Maka dari itu, kasusnya di balik yaituu kedua garis singgung berpotongan di titik (4,-1) dan garis kutub melalui titik (2,-1) seperti gambar di atas. Ini artinya ada kesalahan pengetikan pada soal.
Nomor 12
Bila $ \sin (40^\circ + x ) = a, \, 0^\circ < x < 45^\circ , \, $ maka $ \cos (70^\circ + x ) = .... $
$\spadesuit \, $ gambar dari $ \sin (40^\circ + x ) = a = \frac{a}{1} = \frac{de}{mi} $

Sehingga nilai $ \cos (40^\circ + x ) = \frac{\sqrt{1-a^2}}{1} = \sqrt{1-a^2} $
Konsep dasar : $ \cos ( A + B ) = \cos A \cos B - \sin A \sin B $
$\spadesuit \, $ Menentukan nilai $ \cos (70^\circ + x ) $
$\begin{align} \cos (70^\circ + x ) & = \cos [(30^\circ) + (40^\circ + x) ] \\ = & \cos 30^\circ \cos (40^\circ + x) - \sin 30^\circ \sin (40^\circ + x) \\ & = \frac{1}{2}\sqrt{3} . \sqrt{1-a^2} - \frac{1}{2} . a \\ & = \frac{1}{2} \sqrt{3(1-a^2)} - \frac{1}{2} a \\ \cos (70^\circ + x ) & = \frac{\sqrt{3(1-a^2)} - a}{2} \end{align}$
Jadi, nilai $ \cos (70^\circ + x ) = \frac{\sqrt{3(1-a^2)} - a}{2} . \heartsuit$

Sehingga nilai $ \cos (40^\circ + x ) = \frac{\sqrt{1-a^2}}{1} = \sqrt{1-a^2} $
Konsep dasar : $ \cos ( A + B ) = \cos A \cos B - \sin A \sin B $
$\spadesuit \, $ Menentukan nilai $ \cos (70^\circ + x ) $
$\begin{align} \cos (70^\circ + x ) & = \cos [(30^\circ) + (40^\circ + x) ] \\ = & \cos 30^\circ \cos (40^\circ + x) - \sin 30^\circ \sin (40^\circ + x) \\ & = \frac{1}{2}\sqrt{3} . \sqrt{1-a^2} - \frac{1}{2} . a \\ & = \frac{1}{2} \sqrt{3(1-a^2)} - \frac{1}{2} a \\ \cos (70^\circ + x ) & = \frac{\sqrt{3(1-a^2)} - a}{2} \end{align}$
Jadi, nilai $ \cos (70^\circ + x ) = \frac{\sqrt{3(1-a^2)} - a}{2} . \heartsuit$
Nomor 13
Jika $ A \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] , \, $ dan
$ A \left[ \begin{matrix} -1 \\ 2 \end{matrix} \right] = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] , \, $
maka $ A \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] = .... $
$\spadesuit \, $ Misalkan matriks $ A = \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] $
$\spadesuit \, $ Menentukan matriks $ A \, $ dengan menyelesaikan persamaan
$\begin{align} A \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \, \, \, \, \text{(dari pers(i))} \\ \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \\ \left[ \begin{matrix} a \\ c \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \\ a =2 \, \text{ dan } \, c & = 4 \\ A \left[ \begin{matrix} -1 \\ 2 \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \, \, \, \, \text{(dari pers(ii))} \\ \left[ \begin{matrix} 2 & b \\ 4 & d \end{matrix} \right] \left[ \begin{matrix} -1 \\ 2 \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \\ \left[ \begin{matrix} -2 + 2b \\ -4 + 2d \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \\ -2 + 2b = -5 \rightarrow b & = \frac{-3}{2} \\ -4 + 2d = -6 \rightarrow d & = -1 \end{align}$
Sehingga matriks $ A = \left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \end{matrix} \right] $
$\spadesuit \, $ Menentukan hasil perkaliannya
$\begin{align} A \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] & = \left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \end{matrix} \right] . \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] \\ & = \left[ \begin{matrix} 4 & -19 \\ 8 & -26 \end{matrix} \right] \end{align}$
Jadi, nilai $ A \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] = \left[ \begin{matrix} 4 & -19 \\ 8 & -26 \end{matrix} \right] . \heartsuit $
$\spadesuit \, $ Menentukan matriks $ A \, $ dengan menyelesaikan persamaan
$\begin{align} A \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \, \, \, \, \text{(dari pers(i))} \\ \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \\ \left[ \begin{matrix} a \\ c \end{matrix} \right] & = \left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \\ a =2 \, \text{ dan } \, c & = 4 \\ A \left[ \begin{matrix} -1 \\ 2 \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \, \, \, \, \text{(dari pers(ii))} \\ \left[ \begin{matrix} 2 & b \\ 4 & d \end{matrix} \right] \left[ \begin{matrix} -1 \\ 2 \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \\ \left[ \begin{matrix} -2 + 2b \\ -4 + 2d \end{matrix} \right] & = \left[ \begin{matrix} -5 \\ -6 \end{matrix} \right] \\ -2 + 2b = -5 \rightarrow b & = \frac{-3}{2} \\ -4 + 2d = -6 \rightarrow d & = -1 \end{align}$
Sehingga matriks $ A = \left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \end{matrix} \right] $
$\spadesuit \, $ Menentukan hasil perkaliannya
$\begin{align} A \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] & = \left[ \begin{matrix} 2 & \frac{-3}{2} \\ 4 & -1 \end{matrix} \right] . \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] \\ & = \left[ \begin{matrix} 4 & -19 \\ 8 & -26 \end{matrix} \right] \end{align}$
Jadi, nilai $ A \left[ \begin{matrix} 2 & -5 \\ 0 & 6 \end{matrix} \right] = \left[ \begin{matrix} 4 & -19 \\ 8 & -26 \end{matrix} \right] . \heartsuit $
Nomor 14
Misalkan $A(t)$ menyatakan luas daerah di bawah kurva $y=bx^2 , 0\leq x \leq t$. Jika titik $P(x_0,0)$ sehingga $A(x_0):A(1)=1:8$, maka perbandingan
luas trapesium $ABPQ:DCPQ=...$


$\spadesuit \, $ Menentukan $A(t)$:
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) \\ A(t)& =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)

$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) \\ A(t)& =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)

$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
Nomor 15
Semua nilai $ x \, $ yang memenuhi pertidaksamaan $ {}^{|1-x|} \log (x+5) > 2 \, $ adalah ....
$\spadesuit \, $ Konsep Dasar
Definisi harga mutlak : $|f(x)|^2 = (f(x))^2 $
$ {}^{f(x)}log [g(x)]=h(x) \, $ syarat logaritma : $f(x)>0, f(x)\neq 1, g(x)>0$
Pertidaksamaan Logaritma :
$ {}^{f(x)}log [g(x)] > {}^{f(x)}log [h(x)] \, $ memiliki solusi berdasarkan basisnya
untuk $ 0 < f(x) < 1 \, $ solusinya $ g(x) < h(x) \, $ (tanda dibalik)
untuk $ f(x) > 1 \, $ solusinya $ g(x) > h(x) \, $ (tanda tidak dibalik)
$\spadesuit \, $ Menentukan syarat logaritmanya
$ {}^{|1-x|} \log (x+5) > 2 \, $ memiliki syarat :
syarat basis : $ |1-x| > 0 \rightarrow x \in R , \, x \neq 1 $
$ |1-x| \neq 1 \rightarrow x \neq 0, \, x \neq 2 $
syarat numerus : $ (x+5) > 0 \rightarrow x > -5 $
Sehingga syarat totalnya : HP1 = $ \{ x > -5, \, x \neq 0 , \, x \neq 1, \, x \neq 2 \} $
$\spadesuit \, $ Menyelesaikan pertidaksamaan berdasarkan basisnya yang dibagi menjadi dua kasus
*). untuk $ 0 < |1-x| < 1 \rightarrow \{ 0 < x < 2 \} \, $ (tanda dibalik)
$\begin{align} {}^{|1-x|} \log (x+5) & > 2 \\ {}^{|1-x|} \log (x+5) & > {}^{|1-x|} \log |1-x|^2 \\ (x+5) & < |1-x|^2 \\ (x+5) & < (1-x)^2 \\ x + 5 & < x ^2 -2x + 1 \\ -x^2 + 3x + 4 & < 0 \\ (-x + 4)(x + 1 ) & < 0 \\ x = 4 \vee x & = -1 \end{align}$

pada garis bilangan yang diminta negatif ( < 0 ), solusinya $ \{ x < -1 \vee x > 4 \} $
dari $ \{ 0 < x < 2 \} \, $ dan $ \{ x < -1 \vee x > 4 \} \, $ maka pada kasus ini tidak ada nilai $ x \, $ yang memenuhi.
**). untuk $ |1-x| > 1 \rightarrow \{ x < 0 \vee x > 2 \} \, $ (tanda tidak dibalik)
$\begin{align} {}^{|1-x|} \log (x+5) & > 2 \\ {}^{|1-x|} \log (x+5) & > {}^{|1-x|} \log |1-x|^2 \\ (x+5) & > |1-x|^2 \\ (x+5) & > (1-x)^2 \\ x + 5 & > x ^2 -2x + 1 \\ -x^2 + 3x + 4 & > 0 \\ (-x + 4)(x + 1 ) & > 0 \\ x = 4 \vee x & = -1 \end{align}$
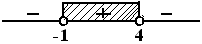
pada garis bilangan yang diminta positif ( > 0 ), solusinya $ \{ -1 < x < 4 \} $
dari $ \{ x < 0 \vee x > 2 \} \, $ dan $ \{ -1 < x < 4 \} \, $ maka pada kasus ini solusinya adalah $ HP2 = \{ -1 < x < 0 \vee 2 < x < 4 \} $
Sehingga solusi totalnya :
$ HP = HP1 \cap HP2 = \{ -1 < x < 0 \vee 2 < x < 4 \} $
Jadi, semua nilai $ x \, $ nya adalah $ \{ -1 < x < 0 \vee 2 < x < 4 \} . \heartsuit$
Definisi harga mutlak : $|f(x)|^2 = (f(x))^2 $
$ {}^{f(x)}log [g(x)]=h(x) \, $ syarat logaritma : $f(x)>0, f(x)\neq 1, g(x)>0$
Pertidaksamaan Logaritma :
$ {}^{f(x)}log [g(x)] > {}^{f(x)}log [h(x)] \, $ memiliki solusi berdasarkan basisnya
untuk $ 0 < f(x) < 1 \, $ solusinya $ g(x) < h(x) \, $ (tanda dibalik)
untuk $ f(x) > 1 \, $ solusinya $ g(x) > h(x) \, $ (tanda tidak dibalik)
$\spadesuit \, $ Menentukan syarat logaritmanya
$ {}^{|1-x|} \log (x+5) > 2 \, $ memiliki syarat :
syarat basis : $ |1-x| > 0 \rightarrow x \in R , \, x \neq 1 $
$ |1-x| \neq 1 \rightarrow x \neq 0, \, x \neq 2 $
syarat numerus : $ (x+5) > 0 \rightarrow x > -5 $
Sehingga syarat totalnya : HP1 = $ \{ x > -5, \, x \neq 0 , \, x \neq 1, \, x \neq 2 \} $
$\spadesuit \, $ Menyelesaikan pertidaksamaan berdasarkan basisnya yang dibagi menjadi dua kasus
*). untuk $ 0 < |1-x| < 1 \rightarrow \{ 0 < x < 2 \} \, $ (tanda dibalik)
$\begin{align} {}^{|1-x|} \log (x+5) & > 2 \\ {}^{|1-x|} \log (x+5) & > {}^{|1-x|} \log |1-x|^2 \\ (x+5) & < |1-x|^2 \\ (x+5) & < (1-x)^2 \\ x + 5 & < x ^2 -2x + 1 \\ -x^2 + 3x + 4 & < 0 \\ (-x + 4)(x + 1 ) & < 0 \\ x = 4 \vee x & = -1 \end{align}$

pada garis bilangan yang diminta negatif ( < 0 ), solusinya $ \{ x < -1 \vee x > 4 \} $
dari $ \{ 0 < x < 2 \} \, $ dan $ \{ x < -1 \vee x > 4 \} \, $ maka pada kasus ini tidak ada nilai $ x \, $ yang memenuhi.
**). untuk $ |1-x| > 1 \rightarrow \{ x < 0 \vee x > 2 \} \, $ (tanda tidak dibalik)
$\begin{align} {}^{|1-x|} \log (x+5) & > 2 \\ {}^{|1-x|} \log (x+5) & > {}^{|1-x|} \log |1-x|^2 \\ (x+5) & > |1-x|^2 \\ (x+5) & > (1-x)^2 \\ x + 5 & > x ^2 -2x + 1 \\ -x^2 + 3x + 4 & > 0 \\ (-x + 4)(x + 1 ) & > 0 \\ x = 4 \vee x & = -1 \end{align}$

pada garis bilangan yang diminta positif ( > 0 ), solusinya $ \{ -1 < x < 4 \} $
dari $ \{ x < 0 \vee x > 2 \} \, $ dan $ \{ -1 < x < 4 \} \, $ maka pada kasus ini solusinya adalah $ HP2 = \{ -1 < x < 0 \vee 2 < x < 4 \} $
Sehingga solusi totalnya :
$ HP = HP1 \cap HP2 = \{ -1 < x < 0 \vee 2 < x < 4 \} $
Jadi, semua nilai $ x \, $ nya adalah $ \{ -1 < x < 0 \vee 2 < x < 4 \} . \heartsuit$