Nomor 11
Jika $ 0 \leq x \leq \pi \, $ , maka himpunan penyelesaian pertaksamaan $ \cos x - \sin 2x < 0 \, $ adalah ....
$\clubsuit \, $ Konsep Trigonometri : $ \sin 2 x = 2\sin x . \cos x $
$\clubsuit \, $ Menyelesaikan soal
$\begin{align} \cos x - \sin 2x & < 0 \\ \cos x - 2\sin x . \cos x & < 0 \\ \cos x (1-2\sin x ) & < 0 \\ \cos x = 0 & \vee \sin x = \frac{1}{2} \\ \cos x = 0 \rightarrow & \, x = \frac{\pi}{2} , \frac{3\pi}{2} \\ \sin x = \frac{1}{2} \rightarrow & \, x = \frac{\pi}{6} , \frac{5\pi}{6} \end{align}$
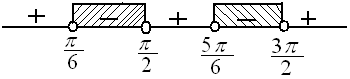
$HP = \{ \frac{\pi}{6} < x < \frac{\pi}{2} \cup \frac{5\pi}{6} < x < \frac{3\pi}{2} \} $
Jadi, solusi yang memenuhi $ 0 \leq x \leq \pi \, $ adalah
$ HP = \{ \frac{\pi}{6} < x < \frac{\pi}{2} \} \cup \{ \frac{5\pi}{6} < x \leq \pi \} . \heartsuit $
$\clubsuit \, $ Menyelesaikan soal
$\begin{align} \cos x - \sin 2x & < 0 \\ \cos x - 2\sin x . \cos x & < 0 \\ \cos x (1-2\sin x ) & < 0 \\ \cos x = 0 & \vee \sin x = \frac{1}{2} \\ \cos x = 0 \rightarrow & \, x = \frac{\pi}{2} , \frac{3\pi}{2} \\ \sin x = \frac{1}{2} \rightarrow & \, x = \frac{\pi}{6} , \frac{5\pi}{6} \end{align}$
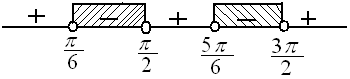
$HP = \{ \frac{\pi}{6} < x < \frac{\pi}{2} \cup \frac{5\pi}{6} < x < \frac{3\pi}{2} \} $
Jadi, solusi yang memenuhi $ 0 \leq x \leq \pi \, $ adalah
$ HP = \{ \frac{\pi}{6} < x < \frac{\pi}{2} \} \cup \{ \frac{5\pi}{6} < x \leq \pi \} . \heartsuit $
Nomor 12
Syarat agar akar-akar persamaan kuadrat $ (p-2)x^2 + 2px + p-1 = 0 \, $ negatif dan berlainan adalah ....
$\spadesuit \, $ PK : $ (p-2)x^2 + 2px + p-1 = 0 $
$ \rightarrow a = p-2, \, b = 2p , \, c = p-1 $
$\spadesuit \, $ Syarat akar-akar negatif dan berlainan
$ x_1+x_2 < 0 , \, x_1.x_2 > 0 , \, $ dan $ \, D > 0 $
$\spadesuit \, $ Menyelesaikan syarat-syaratnya
$\begin{align} \text{syarat I: } \, x_1+x_2 < 0 \rightarrow \frac{-b}{a} & < 0 \\ \frac{-2p}{p-2} & < 0 \\ p=0 & \vee p = 2 \end{align}$
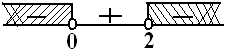
$ HP1 = \{ p < 0 \vee p > 2 \} $
$\begin{align} \text{syarat II: } \, x_1.x_2 > 0 \rightarrow \frac{c}{a} & > 0 \\ \frac{p-1}{p-2} & > 0 \\ p=1 & \vee p = 2 \end{align}$
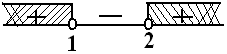
$ HP2 = \{ p < 1 \vee p > 2 \} $
$\begin{align} \text{syarat III: } \, D > 0 \rightarrow b^2 - 4ac & > 0 \\ (2p)^2 - 4(p-2)(p-1) & > 0 \\ 4p^2 - 4p^2 + 12p - 8 & > 0 \\ 12p & > 8 \\ p & > \frac{8}{12} = \frac{2}{3} \\ HP3 & = \{ p > \frac{2}{3} \} \end{align}$
Sehingga solusinya :
$\begin{align} HP & = HP1 \cap HP2 \cap HP3 = \{ p > 2 \} \end{align}$
Jadi, solusinya $ HP = \{ p > 2 \} . \heartsuit $
$ \rightarrow a = p-2, \, b = 2p , \, c = p-1 $
$\spadesuit \, $ Syarat akar-akar negatif dan berlainan
$ x_1+x_2 < 0 , \, x_1.x_2 > 0 , \, $ dan $ \, D > 0 $
$\spadesuit \, $ Menyelesaikan syarat-syaratnya
$\begin{align} \text{syarat I: } \, x_1+x_2 < 0 \rightarrow \frac{-b}{a} & < 0 \\ \frac{-2p}{p-2} & < 0 \\ p=0 & \vee p = 2 \end{align}$
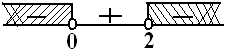
$ HP1 = \{ p < 0 \vee p > 2 \} $
$\begin{align} \text{syarat II: } \, x_1.x_2 > 0 \rightarrow \frac{c}{a} & > 0 \\ \frac{p-1}{p-2} & > 0 \\ p=1 & \vee p = 2 \end{align}$
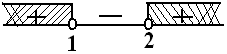
$ HP2 = \{ p < 1 \vee p > 2 \} $
$\begin{align} \text{syarat III: } \, D > 0 \rightarrow b^2 - 4ac & > 0 \\ (2p)^2 - 4(p-2)(p-1) & > 0 \\ 4p^2 - 4p^2 + 12p - 8 & > 0 \\ 12p & > 8 \\ p & > \frac{8}{12} = \frac{2}{3} \\ HP3 & = \{ p > \frac{2}{3} \} \end{align}$
Sehingga solusinya :
$\begin{align} HP & = HP1 \cap HP2 \cap HP3 = \{ p > 2 \} \end{align}$
Jadi, solusinya $ HP = \{ p > 2 \} . \heartsuit $
Nomor 13
Melalui titik ($1, \, -\frac{3}{4}$) dibuat garis singgung pada parabola $ y = \frac{1}{4}x^2 \, $ , absis kedua titik singgungnya adalah ....
$\spadesuit \, $ Misalkan persamaan garis singgungnya :
$ y = mx + b \, \, $ ....pers(i)
$\spadesuit \, $ Substitusi titik ($1, \, -\frac{3}{4}$) ke pers(i)
$\begin{align} (1, \, -\frac{3}{4}) \rightarrow y & = mx + b \\ -\frac{3}{4} & = m.1 + b \\ b & = -m -\frac{3}{4} \end{align}$
Sehingga garisnya menjadi :
$ y = mx + b \rightarrow y = mx -m -\frac{3}{4} \, \, $ ....pers(ii)
$\spadesuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$ y = \frac{1}{4} x^2 \rightarrow y^\prime = \frac{1}{2}x $
sehingga : $ m = f^\prime (x) \rightarrow m = \frac{1}{2}x $
$\spadesuit \, $ Substitusi $ m = \frac{1}{2}x $ ke pers(ii)
$ y = mx -m -\frac{3}{4} \rightarrow y = \frac{1}{2}x.x -\frac{1}{2}x -\frac{3}{4} $
$ y = \frac{1}{2}x^2 -\frac{1}{2}x -\frac{3}{4} \, \, $ ....pers(iii)
$\spadesuit \, $ Karena bersinggungan, maka nilai parabola = garis
$\begin{align} y_1 & = y_2 \\ \frac{1}{4} x^2 & = \frac{1}{2}x^2 -\frac{1}{2}x -\frac{3}{4} \, \, \text{(kali 4)} \\ x^2 & = 2x^2 -2x -3 \\ x^2 - 2x - 3 & = 0 \\ (x+1)(x-3) & = 0 \\ x=-1 & \vee x = 3 \end{align}$
Jadi, absis titik singgungnya adalah $ x = -1 \, $ dan $ x = 3 . \heartsuit $
$ y = mx + b \, \, $ ....pers(i)
$\spadesuit \, $ Substitusi titik ($1, \, -\frac{3}{4}$) ke pers(i)
$\begin{align} (1, \, -\frac{3}{4}) \rightarrow y & = mx + b \\ -\frac{3}{4} & = m.1 + b \\ b & = -m -\frac{3}{4} \end{align}$
Sehingga garisnya menjadi :
$ y = mx + b \rightarrow y = mx -m -\frac{3}{4} \, \, $ ....pers(ii)
$\spadesuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$ y = \frac{1}{4} x^2 \rightarrow y^\prime = \frac{1}{2}x $
sehingga : $ m = f^\prime (x) \rightarrow m = \frac{1}{2}x $
$\spadesuit \, $ Substitusi $ m = \frac{1}{2}x $ ke pers(ii)
$ y = mx -m -\frac{3}{4} \rightarrow y = \frac{1}{2}x.x -\frac{1}{2}x -\frac{3}{4} $
$ y = \frac{1}{2}x^2 -\frac{1}{2}x -\frac{3}{4} \, \, $ ....pers(iii)
$\spadesuit \, $ Karena bersinggungan, maka nilai parabola = garis
$\begin{align} y_1 & = y_2 \\ \frac{1}{4} x^2 & = \frac{1}{2}x^2 -\frac{1}{2}x -\frac{3}{4} \, \, \text{(kali 4)} \\ x^2 & = 2x^2 -2x -3 \\ x^2 - 2x - 3 & = 0 \\ (x+1)(x-3) & = 0 \\ x=-1 & \vee x = 3 \end{align}$
Jadi, absis titik singgungnya adalah $ x = -1 \, $ dan $ x = 3 . \heartsuit $
Cara II : Menentukan nilai $ m $ (gradiennya)
$\spadesuit \, $ Misalkan persamaan garis singgungnya :
$ y = mx + b \, \, $ ....pers(i)
$\spadesuit \, $ Substitusi titik ($1, \, -\frac{3}{4}$) ke pers(i)
$\begin{align} (1, \, -\frac{3}{4}) \rightarrow y & = mx + b \\ -\frac{3}{4} & = m.1 + b \\ b & = -m -\frac{3}{4} \end{align}$
Sehingga garisnya menjadi :
$ y = mx + b \rightarrow y = mx -m -\frac{3}{4} \, \, $ ....pers(ii)
$\spadesuit \, $ Syarat bersinggungan : $ D = 0 $
$\begin{align} y_1 & = y_2 \\ \frac{1}{4} x^2 & = mx -m -\frac{3}{4} \, \, \text{(kali 4)} \\ x^2 & = 4mx - 4m - 3 \\ x^2 - 4mx +4m + 3 & = 0 \\ D & = 0 \, \, \text{(syarat garis singgung)} \\ b^2 - 4ac & = 0 \\ (-4m)^2 - 4.1.(4m+3) & = 0 \\ 16m^2 -16m -12 & = 0 \\ 4m^2 - 4m - 4 & = 0 \\ (2m+1)(2m-3) & = 0 \\ m = \frac{-1}{2} & \vee m = \frac{3}{2} \end{align}$
$\spadesuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$ y = \frac{1}{4} x^2 \rightarrow y^\prime = \frac{1}{2}x $
sehingga : $ m = f^\prime (x) \rightarrow m = \frac{1}{2}x $
untuk $ m = \frac{-1}{2} \rightarrow \frac{-1}{2} = \frac{1}{2}x \rightarrow x = -1 $
untuk $ m = \frac{3}{2} \rightarrow \frac{3}{2} = \frac{1}{2}x \rightarrow x = 3 $
Jadi, absis titik singgungnya adalah $ x = -1 \, $ dan $ x = 3 . \heartsuit $
$\spadesuit \, $ Misalkan persamaan garis singgungnya :
$ y = mx + b \, \, $ ....pers(i)
$\spadesuit \, $ Substitusi titik ($1, \, -\frac{3}{4}$) ke pers(i)
$\begin{align} (1, \, -\frac{3}{4}) \rightarrow y & = mx + b \\ -\frac{3}{4} & = m.1 + b \\ b & = -m -\frac{3}{4} \end{align}$
Sehingga garisnya menjadi :
$ y = mx + b \rightarrow y = mx -m -\frac{3}{4} \, \, $ ....pers(ii)
$\spadesuit \, $ Syarat bersinggungan : $ D = 0 $
$\begin{align} y_1 & = y_2 \\ \frac{1}{4} x^2 & = mx -m -\frac{3}{4} \, \, \text{(kali 4)} \\ x^2 & = 4mx - 4m - 3 \\ x^2 - 4mx +4m + 3 & = 0 \\ D & = 0 \, \, \text{(syarat garis singgung)} \\ b^2 - 4ac & = 0 \\ (-4m)^2 - 4.1.(4m+3) & = 0 \\ 16m^2 -16m -12 & = 0 \\ 4m^2 - 4m - 4 & = 0 \\ (2m+1)(2m-3) & = 0 \\ m = \frac{-1}{2} & \vee m = \frac{3}{2} \end{align}$
$\spadesuit \, $ Gradien garis singgung : $ m = f^\prime (x) $
$ y = \frac{1}{4} x^2 \rightarrow y^\prime = \frac{1}{2}x $
sehingga : $ m = f^\prime (x) \rightarrow m = \frac{1}{2}x $
untuk $ m = \frac{-1}{2} \rightarrow \frac{-1}{2} = \frac{1}{2}x \rightarrow x = -1 $
untuk $ m = \frac{3}{2} \rightarrow \frac{3}{2} = \frac{1}{2}x \rightarrow x = 3 $
Jadi, absis titik singgungnya adalah $ x = -1 \, $ dan $ x = 3 . \heartsuit $
Nomor 14
Diketahui $ p(x) = ax^5 + bx -1 \, $ dengan $ a $ dan $ b $ adalah konstan. Jika $ p(x) $ dibagi $ (x-2006) $ bersisa 3, maka bila
$ p(x) $ dibagi dengan $ (x+2006) $ akan bersisa ....
$\spadesuit \, $ Teorema sisa : $ \frac{P(x)}{x+a} \rightarrow \, \text{sisa} \, = P(-a) $
$\spadesuit \, $ Pembagian $ p(x) = ax^5 + bx -1 \, $ dibagi ($x-2006$),
dengan sisa = 3
$ \frac{p(x)}{x-2006} \rightarrow \, \text{sisa} \, = p(2006) \rightarrow 3 = p(2006)$
Diperoleh :
$\begin{align} p(2006) = 3 \rightarrow a(2006)^5 + b.(2006) -1 & = 3 \\ a(2006)^5 + b(2006) & = 4 \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Pembagian $ p(x) = ax^5 + bx -1 \, $ dibagi ($x+2006$)
$ \frac{p(x)}{x+2006} \rightarrow \, \text{sisa} \, = p(-2006) $
Diperoleh :
$\begin{align} \text{sisa} \, & = p(-2006) \\ & = a(-2006)^5 + b(-2006) -1 \\ & = -a(2006)^5 - b(2006) -1 \\ & = -[a(2006)^5 + b(2006)] -1 \, \, \, \, \text{[dari pers(i)]} \\ & = -[4] -1 \\ & = -5 \end{align}$
Jadi, sisa pembagiannya adalah -5. $ \heartsuit $
$\spadesuit \, $ Pembagian $ p(x) = ax^5 + bx -1 \, $ dibagi ($x-2006$),
dengan sisa = 3
$ \frac{p(x)}{x-2006} \rightarrow \, \text{sisa} \, = p(2006) \rightarrow 3 = p(2006)$
Diperoleh :
$\begin{align} p(2006) = 3 \rightarrow a(2006)^5 + b.(2006) -1 & = 3 \\ a(2006)^5 + b(2006) & = 4 \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Pembagian $ p(x) = ax^5 + bx -1 \, $ dibagi ($x+2006$)
$ \frac{p(x)}{x+2006} \rightarrow \, \text{sisa} \, = p(-2006) $
Diperoleh :
$\begin{align} \text{sisa} \, & = p(-2006) \\ & = a(-2006)^5 + b(-2006) -1 \\ & = -a(2006)^5 - b(2006) -1 \\ & = -[a(2006)^5 + b(2006)] -1 \, \, \, \, \text{[dari pers(i)]} \\ & = -[4] -1 \\ & = -5 \end{align}$
Jadi, sisa pembagiannya adalah -5. $ \heartsuit $
Nomor 15
Jika $ \, \frac{8^x}{2^y} = 32 \, $ dan $ \, 4^x.2^y = 32^2 \, , $ maka $ \, x+y = .... $
$\clubsuit \, $ Sifat eksponen :
$ a^m.a^n = a^{m+n}, \, \frac{a^m}{a^n} = a^{m-n} \, $ dan $ (a^m)^n = a^{mn} $
$\clubsuit \, $ Menyederhanakan soal
Persamaan pertama :
$\begin{align} \frac{8^x}{2^y} = 32 \rightarrow \frac{(2^3)^x}{2^y} & = 2^5 \\ \frac{2^{3x}}{2^y} = 2^5 \rightarrow 2^{3x-y} & = 2^5 \\ 3x-y & = 5 \, \, \text{...pers(i)} \end{align}$
Persamaan kedua :
$\begin{align} 4^x.2^y = 32^2 \rightarrow (2^2)^x.2^y & = (2^5)^2 \\ \frac{2^{2x}}{2^y} = 2^{10} \rightarrow 2^{2x+y} & = 2^{10} \\ 2x+y & = 10 \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 3x-y = 5 & \\ 2x+y = 10 & + \\ \hline 5x = 15 & \\ x = 3 & \end{array}$
pers(ii): $ 2x+y = 10 \rightarrow 2.3 +y = 10 \rightarrow y = 4 $
Sehingga nilai $ x + y = 3 + 4 = 7 $
Jadi, nilai $ x + y = 7. \heartsuit $
$ a^m.a^n = a^{m+n}, \, \frac{a^m}{a^n} = a^{m-n} \, $ dan $ (a^m)^n = a^{mn} $
$\clubsuit \, $ Menyederhanakan soal
Persamaan pertama :
$\begin{align} \frac{8^x}{2^y} = 32 \rightarrow \frac{(2^3)^x}{2^y} & = 2^5 \\ \frac{2^{3x}}{2^y} = 2^5 \rightarrow 2^{3x-y} & = 2^5 \\ 3x-y & = 5 \, \, \text{...pers(i)} \end{align}$
Persamaan kedua :
$\begin{align} 4^x.2^y = 32^2 \rightarrow (2^2)^x.2^y & = (2^5)^2 \\ \frac{2^{2x}}{2^y} = 2^{10} \rightarrow 2^{2x+y} & = 2^{10} \\ 2x+y & = 10 \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 3x-y = 5 & \\ 2x+y = 10 & + \\ \hline 5x = 15 & \\ x = 3 & \end{array}$
pers(ii): $ 2x+y = 10 \rightarrow 2.3 +y = 10 \rightarrow y = 4 $
Sehingga nilai $ x + y = 3 + 4 = 7 $
Jadi, nilai $ x + y = 7. \heartsuit $