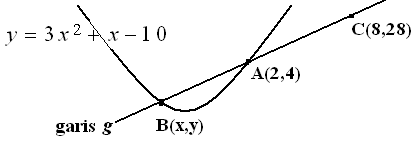
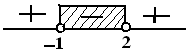
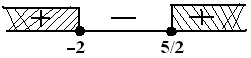Nomor 21
Jika $A=\left( \begin{matrix} 1 & 2 \\ 1 & 3 \end{matrix} \right) $ , $B=\left( \begin{matrix} 4 & 1 \\ 1 & 3 \end{matrix} \right) $
dan matriks C memenuhi AC = B, maka det C = ....
$\spadesuit \, $ Sifat determinan : $|PQ| = |P|.|Q| $
$A=\left( \begin{matrix} 1 & 2 \\ 1 & 3 \end{matrix} \right) \rightarrow |A| = 1.3-1.2 = 3-2=1 $
$B=\left( \begin{matrix} 4 & 1 \\ 1 & 3 \end{matrix} \right) \rightarrow |B| = 4.3-1.1 = 12-1 = 11 $
$\spadesuit \, $ Menentukan determinan C dengan sifat determinan
$\begin{align} AC & = B \\ |AC| & = |B| \\ |A|.|C| & = |B| \\ 1. |C| & = 11 \\ |C| & = \frac{11}{1} = 11 \end{align}$
Jadi, determinan C adalah 11. $ \heartsuit $
$A=\left( \begin{matrix} 1 & 2 \\ 1 & 3 \end{matrix} \right) \rightarrow |A| = 1.3-1.2 = 3-2=1 $
$B=\left( \begin{matrix} 4 & 1 \\ 1 & 3 \end{matrix} \right) \rightarrow |B| = 4.3-1.1 = 12-1 = 11 $
$\spadesuit \, $ Menentukan determinan C dengan sifat determinan
$\begin{align} AC & = B \\ |AC| & = |B| \\ |A|.|C| & = |B| \\ 1. |C| & = 11 \\ |C| & = \frac{11}{1} = 11 \end{align}$
Jadi, determinan C adalah 11. $ \heartsuit $
Nomor 22
Tabungan seseorang pada bulang ke $n $ selalu dua kali tabungan pada bulan ke ($n-1$) , $n \geq 2 $ . Jika tabungan awalnya
Rp. 1 juta dan setelah satu tahun menjadi Rp. $p $ juta, maka $p $ memenuhi ....
$\clubsuit \, $ Barisan geometri : $U_n=ar^{n-1} $
$\clubsuit \, $ Tabungan awal 1 juta , $a = 1 \, \, $ juta
$\clubsuit \, $ Tabungan bulan ke-$n $ dua kali tabungan bulan ke-($n-1 $) , artinya $ r = 2 $
$\clubsuit \, $ Setelah satu tahun, artinya bulan ke-13
$U_{13} = ar^{12} = 1. 2^{12} = 4096 \rightarrow p = 4096 \, \, $ juta
Jadi, yang memenuhi $ 4000 < p < 5000 . \heartsuit $
$\clubsuit \, $ Tabungan awal 1 juta , $a = 1 \, \, $ juta
$\clubsuit \, $ Tabungan bulan ke-$n $ dua kali tabungan bulan ke-($n-1 $) , artinya $ r = 2 $
$\clubsuit \, $ Setelah satu tahun, artinya bulan ke-13
$U_{13} = ar^{12} = 1. 2^{12} = 4096 \rightarrow p = 4096 \, \, $ juta
Jadi, yang memenuhi $ 4000 < p < 5000 . \heartsuit $
Nomor 23
Jika $y = \log x $ dan $x^2+ax+(3-a) = 0 $ , maka $y $ bernilai real untuk $a $ yang memenuhi ....
$\spadesuit \, $ Fungsi $y = \log x \, \, $ bernilai positif jika $x > 0 \, $ (positif)
Karena $x>0 \, \, $ dan merupakan akar-akar dari $x^2+ax+(3-a) = 0 $ maka harus $x_1>0 \, $ dan $x_2 > 0 \, $ (akar-akar positif)
$x_1+x_2 = \frac{-b}{a} = \frac{-a}{1} = -a \, \, $ dan $ x_1.x_2 = \frac{c}{a} = \frac{3-a}{1} = 3-a $
$\spadesuit \, $ Syarat akar-akar positif : $ x_1+x_2 > 0 , \, x_1.x_2 > 0 \, \, $ dan $ D \geq 0 $
$\spadesuit \, $ Menyelesaikan syaratnya
$\begin{align} * \, x_1+x_2 & > 0 \\ -a & > 0 \\ a & < 0 \, \, \, \text{(HP}_1) \end{align}$
$\begin{align} * \, x_1.x_2 & > 0 \\ 3-a & > 0 \\ a & < 3 \, \, \, \text{(HP}_2) \end{align}$
$\begin{align} \text{Syarat nilai } \, \, D & \geq 0 \\ b^2-4ac & \geq 0 \\ (-a)^2 - 4.1.(3-a) & \geq 0 \\ a^2+4a-12 &\geq 0 \\ (a-2)(a+6) & \geq 0 \\ a = 2 & \vee a = -6 \end{align}$

HP$_3 = \{ a \leq -6 \vee a \geq 2 \} $
Solusinya : $HP = HP_1\cap HP_2 \cap HP_3 = \{ a \leq -6 \} $
Jadi, nilai $a \, \, $ yang memenuhi adalah $ \{ a \leq -6 \}. \heartsuit $
Karena $x>0 \, \, $ dan merupakan akar-akar dari $x^2+ax+(3-a) = 0 $ maka harus $x_1>0 \, $ dan $x_2 > 0 \, $ (akar-akar positif)
$x_1+x_2 = \frac{-b}{a} = \frac{-a}{1} = -a \, \, $ dan $ x_1.x_2 = \frac{c}{a} = \frac{3-a}{1} = 3-a $
$\spadesuit \, $ Syarat akar-akar positif : $ x_1+x_2 > 0 , \, x_1.x_2 > 0 \, \, $ dan $ D \geq 0 $
$\spadesuit \, $ Menyelesaikan syaratnya
$\begin{align} * \, x_1+x_2 & > 0 \\ -a & > 0 \\ a & < 0 \, \, \, \text{(HP}_1) \end{align}$
$\begin{align} * \, x_1.x_2 & > 0 \\ 3-a & > 0 \\ a & < 3 \, \, \, \text{(HP}_2) \end{align}$
$\begin{align} \text{Syarat nilai } \, \, D & \geq 0 \\ b^2-4ac & \geq 0 \\ (-a)^2 - 4.1.(3-a) & \geq 0 \\ a^2+4a-12 &\geq 0 \\ (a-2)(a+6) & \geq 0 \\ a = 2 & \vee a = -6 \end{align}$

HP$_3 = \{ a \leq -6 \vee a \geq 2 \} $
Solusinya : $HP = HP_1\cap HP_2 \cap HP_3 = \{ a \leq -6 \} $
Jadi, nilai $a \, \, $ yang memenuhi adalah $ \{ a \leq -6 \}. \heartsuit $
Nomor 24
Bilangan ${}^y \log (x-1), \, {}^y \log (x+1), \, {}^y \log (3x-1) $ merupakan tiga suku deret aritmetika yang berurutan.
Jika jumlah tiga bilangan itu adalah 6, maka $x+y = ....$
$\clubsuit \,$ Syarat logaritma
${}^y \log (x-1) \rightarrow x-1 > 0 \rightarrow x > 1 $
${}^y \log (x+1) \rightarrow x+1 > 0 \rightarrow x > -1 $
${}^y \log (3x-1) \rightarrow 3x-1 > 0 \rightarrow x > \frac{1}{3} $
Syarat yang memenuhi ketiganya adalah $\{ x > 1 \} $
$\clubsuit \, $ Barisan aritmetika : ${}^y \log (x-1), \, {}^y \log (x+1), \, {}^y \log (3x-1) $
$\begin{align} {}^y \log (x+1) - {}^y \log (x-1) & = {}^y \log (3x-1) - {}^y \log (x+1) \\ {}^y \log \frac{x+1}{x-1} & = {}^y \log \frac{3x-1}{x+1} \\ \frac{x+1}{x-1} & = \frac{3x-1}{x+1} \\ (x+1)^2 & = (3x-1)(x-1) \\ 2x^2 - 6x & = 0 \\ 2x(x-3) & = 0 \\ x=3 \vee x = 0 & \, \, \text{(Tidak memenuhi karena harus } \, x > 1 ) \end{align}$
$\clubsuit \, $ Jumlah ketiganya sama dengan 6
$\begin{align} {}^y \log (x-1) + {}^y \log (x+1) + {}^y \log (3x-1) & = 6 \\ {}^y \log (x-1).(x+1).(3x-1) & = 6 \\ {}^y \log (3-1).(3+1).(3.3-1) & = 6 \\ {}^y \log 2.4.8 & = 6 \\ {}^y \log 64 & = 6 \\ y^6 & = 64 \\ y^6 & = 2^6 \rightarrow y=2 \end{align}$
Sehingga : $x+y = 3+2 = 5$
Jadi, nilai $ x+y=5. \heartsuit $
${}^y \log (x-1) \rightarrow x-1 > 0 \rightarrow x > 1 $
${}^y \log (x+1) \rightarrow x+1 > 0 \rightarrow x > -1 $
${}^y \log (3x-1) \rightarrow 3x-1 > 0 \rightarrow x > \frac{1}{3} $
Syarat yang memenuhi ketiganya adalah $\{ x > 1 \} $
$\clubsuit \, $ Barisan aritmetika : ${}^y \log (x-1), \, {}^y \log (x+1), \, {}^y \log (3x-1) $
$\begin{align} {}^y \log (x+1) - {}^y \log (x-1) & = {}^y \log (3x-1) - {}^y \log (x+1) \\ {}^y \log \frac{x+1}{x-1} & = {}^y \log \frac{3x-1}{x+1} \\ \frac{x+1}{x-1} & = \frac{3x-1}{x+1} \\ (x+1)^2 & = (3x-1)(x-1) \\ 2x^2 - 6x & = 0 \\ 2x(x-3) & = 0 \\ x=3 \vee x = 0 & \, \, \text{(Tidak memenuhi karena harus } \, x > 1 ) \end{align}$
$\clubsuit \, $ Jumlah ketiganya sama dengan 6
$\begin{align} {}^y \log (x-1) + {}^y \log (x+1) + {}^y \log (3x-1) & = 6 \\ {}^y \log (x-1).(x+1).(3x-1) & = 6 \\ {}^y \log (3-1).(3+1).(3.3-1) & = 6 \\ {}^y \log 2.4.8 & = 6 \\ {}^y \log 64 & = 6 \\ y^6 & = 64 \\ y^6 & = 2^6 \rightarrow y=2 \end{align}$
Sehingga : $x+y = 3+2 = 5$
Jadi, nilai $ x+y=5. \heartsuit $
Nomor 25
Berat rata-rata 10 siswa adalah 60 kg. Salah seorang diantaranya diganti oleh Andi sehingga berat rata-ratanya menjadi 60,5 kg.
Jika berat Andi 62 kg, maka berat siswa yang diganti adalah ....
$\spadesuit \, $ Misalkan total nilai 9 orang adalah $N \, $ dan nilai orang yang digantikan adalah $x$
$\spadesuit \, $ Rata-rata semula 60 kg
$\frac{N+x}{10} = 60 \rightarrow N+x = 600 \, \, \, $ ...pers(i)
$\spadesuit \, $ Rata-rata kedua 60,5 kg dengan berat Andi = 62 kg
$\frac{N+A}{10} = 60,5 \rightarrow N+62 = 605 \rightarrow N = 605 - 62 = 543 $
$\spadesuit \, $ Substitusi nilai $N=543 \, $ ke pers(i)
$N+x = 600 \rightarrow 543 + x = 600 \rightarrow x = 600-543 = 57 $
Jadi, berat siswa yang diganti adalah 57. $ \heartsuit $
$\spadesuit \, $ Rata-rata semula 60 kg
$\frac{N+x}{10} = 60 \rightarrow N+x = 600 \, \, \, $ ...pers(i)
$\spadesuit \, $ Rata-rata kedua 60,5 kg dengan berat Andi = 62 kg
$\frac{N+A}{10} = 60,5 \rightarrow N+62 = 605 \rightarrow N = 605 - 62 = 543 $
$\spadesuit \, $ Substitusi nilai $N=543 \, $ ke pers(i)
$N+x = 600 \rightarrow 543 + x = 600 \rightarrow x = 600-543 = 57 $
Jadi, berat siswa yang diganti adalah 57. $ \heartsuit $