Nomor 11
Garis singgung kurva $ f(x) = -x^2 + 2\sqrt{x} \, $ di titik (4,-12) memotong sumbu X dan sumbu Y masing-masing di titik
$(p,0) $ dan $(0,q)$. Nilai $ q - 5p = .... $
$ \clubsuit \, $ Konsep Garis singgung
Persamaan garis singgung (PGS) pada kurva $ y = f(x) \, $ di titik $(x_1,y_1) \, $ adalah $ y - y_1 = m(x-x_1) \, $ dengan $ m = f^\prime (x_1) $.
$ \clubsuit \, $ Menentukan gradien $(m) \, $ di titik $(x_1,y_1) = (4,-12) $
$\begin{align} f(x) & = -x^2 + 2\sqrt{x} \\ f^\prime (x) & = -2x + 2\frac{1}{2\sqrt{x}} \\ f^\prime (x) & = -2x + \frac{1}{\sqrt{x}} \\ m & = f^\prime (x_1) = f^\prime (4) \\ m & = -2.4 + \frac{1}{\sqrt{4}} \\ & = -8 + \frac{1}{2} \\ & = - \frac{15}{2} \end{align}$
$ \clubsuit \, $ Menentukan PGS
$\begin{align} y - y_1 & = m(x-x_1) \\ y - (-12) & = - \frac{15}{2} (x-4) \\ y + 12 & = - \frac{15}{2} (x-4) \end{align}$
$ \clubsuit \, $ Memotong sumbu X, substitusi $ y = 0 $
$\begin{align} y = 0 \rightarrow y + 12 & = - \frac{15}{2} (x-4) \\ 0 + 12 & = - \frac{15}{2} (x-4) \\ 24 & = -15x + 60 \\ 15x & = 36 \\ x & = \frac{36}{15} = \frac{12}{5} \end{align}$
titiknya : $ (p,0) = (\frac{12}{5} , 0) \, $ artinya $ p = \frac{12}{5} $.
$ \clubsuit \, $ Memotong sumbu Y, substitusi $ x = 0 $
$\begin{align} x = 0 \rightarrow y + 12 & = - \frac{15}{2} (x-4) \\ y + 12 & = - \frac{15}{2} (0-4) \\ y + 12 & = 30 \\ y & = 18 \\ \end{align}$
titiknya : $ (0,q) = (0,18) \, $ artinya $ q = 18 $.
Sehingga nilai : $ q - 5p = 18 - 5.(\frac{12}{5}) = 6 $
Jadi, nilai $ q - 5p = 6. \, \heartsuit $
Persamaan garis singgung (PGS) pada kurva $ y = f(x) \, $ di titik $(x_1,y_1) \, $ adalah $ y - y_1 = m(x-x_1) \, $ dengan $ m = f^\prime (x_1) $.
$ \clubsuit \, $ Menentukan gradien $(m) \, $ di titik $(x_1,y_1) = (4,-12) $
$\begin{align} f(x) & = -x^2 + 2\sqrt{x} \\ f^\prime (x) & = -2x + 2\frac{1}{2\sqrt{x}} \\ f^\prime (x) & = -2x + \frac{1}{\sqrt{x}} \\ m & = f^\prime (x_1) = f^\prime (4) \\ m & = -2.4 + \frac{1}{\sqrt{4}} \\ & = -8 + \frac{1}{2} \\ & = - \frac{15}{2} \end{align}$
$ \clubsuit \, $ Menentukan PGS
$\begin{align} y - y_1 & = m(x-x_1) \\ y - (-12) & = - \frac{15}{2} (x-4) \\ y + 12 & = - \frac{15}{2} (x-4) \end{align}$
$ \clubsuit \, $ Memotong sumbu X, substitusi $ y = 0 $
$\begin{align} y = 0 \rightarrow y + 12 & = - \frac{15}{2} (x-4) \\ 0 + 12 & = - \frac{15}{2} (x-4) \\ 24 & = -15x + 60 \\ 15x & = 36 \\ x & = \frac{36}{15} = \frac{12}{5} \end{align}$
titiknya : $ (p,0) = (\frac{12}{5} , 0) \, $ artinya $ p = \frac{12}{5} $.
$ \clubsuit \, $ Memotong sumbu Y, substitusi $ x = 0 $
$\begin{align} x = 0 \rightarrow y + 12 & = - \frac{15}{2} (x-4) \\ y + 12 & = - \frac{15}{2} (0-4) \\ y + 12 & = 30 \\ y & = 18 \\ \end{align}$
titiknya : $ (0,q) = (0,18) \, $ artinya $ q = 18 $.
Sehingga nilai : $ q - 5p = 18 - 5.(\frac{12}{5}) = 6 $
Jadi, nilai $ q - 5p = 6. \, \heartsuit $
Nomor 12
Jika diberikan
$ \left[ \begin{matrix} 2x-5 & 1 \\ 8 & 5^{-4+3y} \end{matrix} \right] =
\left[ \begin{matrix} 3 & 1 \\ 8 & 25 \end{matrix} \right] $
maka nilai dari $ 2x - 3y \, $ adalah ....
maka nilai dari $ 2x - 3y \, $ adalah ....
$\spadesuit \, $ Menyusun persamaan :
$ \left[ \begin{matrix} 2x-5 & 1 \\ 8 & 5^{-4+3y} \end{matrix} \right] = \left[ \begin{matrix} 3 & 1 \\ 8 & 25 \end{matrix} \right] $
Persamaan pertama :
$\begin{align} 2x-5 & = 3 \rightarrow 2x = 8 \rightarrow x = 4 \end{align}$
Persamaan kedua :
$\begin{align} 5^{-4+3y} & = 25 \\ 5^{-4+3y} & = 5^2 \\ -4+3y & = 2 \\ 3y & = 6 \\ y & = 2 \end{align}$
Sehingga nilai : $ 2x - 3y = 2.4 - 3.2 = 8 - 6 = 2 $.
Jadi, nilai $ 2x - 3y = 2 \, $ (tidak ada di pilihan) . $\heartsuit $
$ \left[ \begin{matrix} 2x-5 & 1 \\ 8 & 5^{-4+3y} \end{matrix} \right] = \left[ \begin{matrix} 3 & 1 \\ 8 & 25 \end{matrix} \right] $
Persamaan pertama :
$\begin{align} 2x-5 & = 3 \rightarrow 2x = 8 \rightarrow x = 4 \end{align}$
Persamaan kedua :
$\begin{align} 5^{-4+3y} & = 25 \\ 5^{-4+3y} & = 5^2 \\ -4+3y & = 2 \\ 3y & = 6 \\ y & = 2 \end{align}$
Sehingga nilai : $ 2x - 3y = 2.4 - 3.2 = 8 - 6 = 2 $.
Jadi, nilai $ 2x - 3y = 2 \, $ (tidak ada di pilihan) . $\heartsuit $
Nomor 13
Luas daerah A yang dibatasi oleh grafik $ y = x^2, \, y = x^2 - 20x + 100 \, $ dan $ y = 0 \, $ dapat dinyatakan sebagai ...
A). $ \int \limits_0^{10} (2x^2 - 20x + 100) dx $
B). $ \int \limits_0^{10} ( 20x - 100) dx $
C). $ \int \limits_0^{5} x^2 dx - \int \limits_5^{10} ( 20x - 100) dx $
D). $ \int \limits_0^{5} x^2 dx + \int \limits_0^{10} ( x^2 - 20x + 100) dx $
E). $ \int \limits_0^{5} x^2 dx + \int \limits_5^{10} ( x^2 - 20x + 100) dx $
A). $ \int \limits_0^{10} (2x^2 - 20x + 100) dx $
B). $ \int \limits_0^{10} ( 20x - 100) dx $
C). $ \int \limits_0^{5} x^2 dx - \int \limits_5^{10} ( 20x - 100) dx $
D). $ \int \limits_0^{5} x^2 dx + \int \limits_0^{10} ( x^2 - 20x + 100) dx $
E). $ \int \limits_0^{5} x^2 dx + \int \limits_5^{10} ( x^2 - 20x + 100) dx $
$\clubsuit \,$ Menggambar grafik fungsi kuadratnya
*). fungsi $ y = x^2 \, $ menyinggung sumbu X di 0 dan hadap atas karena $ a = 1 > 0 $.
*). fungsi $ y = x^2 - 20x + 100 \, $ menyinggung sumbu X di 10 dan hadap atas karena $ a = 1 > 0 $.
*). fungsi $ y = 0 \, $ berupa garis yaitu sumbu X itu sendiri.
$\clubsuit \,$ titik potong kedua kurva
$\begin{align} y_1 & = y_2 \\ x^2 & = x^2 - 20x + 100 \\ 20x & = 100 \\ x & = 5 \end{align} $
Ilustrasi gambarnya :
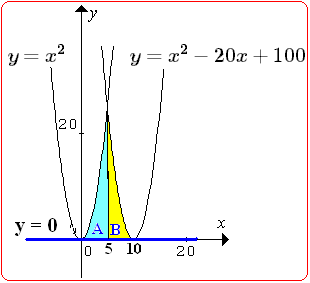
Dari gambar ini, daerah yang dibatasi oleh ketiga kurva dibagi menjadi dua yaitu daerah A dan daerah B.
$\clubsuit \,$ Menentukan luas daerah arsiran
$\begin{align} \text{Luas total } & = L_A + L_B \\ & = \int \limits_{0}^{5} x^2 dx + \int \limits_{5}^{10} x^2 - 20x + 100 dx \end{align} $
Jadi, luas daerahnya adalah $ \int \limits_{0}^{5} x^2 dx + \int \limits_{5}^{10} x^2 - 20x + 100 dx . \, \heartsuit $
*). fungsi $ y = x^2 \, $ menyinggung sumbu X di 0 dan hadap atas karena $ a = 1 > 0 $.
*). fungsi $ y = x^2 - 20x + 100 \, $ menyinggung sumbu X di 10 dan hadap atas karena $ a = 1 > 0 $.
*). fungsi $ y = 0 \, $ berupa garis yaitu sumbu X itu sendiri.
$\clubsuit \,$ titik potong kedua kurva
$\begin{align} y_1 & = y_2 \\ x^2 & = x^2 - 20x + 100 \\ 20x & = 100 \\ x & = 5 \end{align} $
Ilustrasi gambarnya :

Dari gambar ini, daerah yang dibatasi oleh ketiga kurva dibagi menjadi dua yaitu daerah A dan daerah B.
$\clubsuit \,$ Menentukan luas daerah arsiran
$\begin{align} \text{Luas total } & = L_A + L_B \\ & = \int \limits_{0}^{5} x^2 dx + \int \limits_{5}^{10} x^2 - 20x + 100 dx \end{align} $
Jadi, luas daerahnya adalah $ \int \limits_{0}^{5} x^2 dx + \int \limits_{5}^{10} x^2 - 20x + 100 dx . \, \heartsuit $
Nomor 14
Pertaksamaan $ \frac{x^2 + 2x - 15}{2x^2 + 11x + 5} \leq 0 \, $ berlaku untuk ....
$\spadesuit \, $ Menyelesaikan pertidaksamaan
$\begin{align} \frac{x^2 + 2x - 15}{2x^2 + 11x + 5} & \leq 0 \\ \frac{(x-3)(x+5)}{(2x+1)(x+5)} & \leq 0 \\ x = 3, \, x = -5 , \, x & = -\frac{1}{2} \end{align}$
Keterangan :
Akar-akar penyebut tidak boleh ikut $( x = -5, x = -\frac{1}{2} ) $ .

Karena yang diminta $ \leq 0 \, $ , maka daerah yang diarsir adalah daerah bertanda negatif. Sehingga solusinya $ HP = \{ -\frac{1}{2} < x \leq 3 \} $
Jadi, solusinya $ \, HP = \{ -\frac{1}{2} < x \leq 3 \} . \, \heartsuit $
$\begin{align} \frac{x^2 + 2x - 15}{2x^2 + 11x + 5} & \leq 0 \\ \frac{(x-3)(x+5)}{(2x+1)(x+5)} & \leq 0 \\ x = 3, \, x = -5 , \, x & = -\frac{1}{2} \end{align}$
Keterangan :
Akar-akar penyebut tidak boleh ikut $( x = -5, x = -\frac{1}{2} ) $ .

Karena yang diminta $ \leq 0 \, $ , maka daerah yang diarsir adalah daerah bertanda negatif. Sehingga solusinya $ HP = \{ -\frac{1}{2} < x \leq 3 \} $
Jadi, solusinya $ \, HP = \{ -\frac{1}{2} < x \leq 3 \} . \, \heartsuit $
Nomor 15
Dalam himpunan penyelesaian yang memenuhi seistem pertaksamaan $ x \geq 1, \, y \geq 3, \, x + y \leq 8 \, $
dan $ 2x + 3y \leq 20, \, $ nilai minimum dari fungsi $ f(x,y) = 3x + 2y \, $ adalah ....
$\clubsuit \,$ Menggambar Daerah Himpunan Penyelesaiannya (DHP)
*). Gambar garis kedua persamaan :
$ x + y = 8 \rightarrow (0,8) , \, (8,0) $
$ 2x + 3y = 20 \rightarrow (0,\frac{20}{3}) , \, (10,0) $
garis $ x = 1 \, $ adalah garis tegak.
garis $ y = 3 \, $ adalah garis mendatar.
*). Titik potong kedua garis, eliminasi kedua persamaan :
$ \begin{array}{c|c|cc} 2x + 3y = 20 & \times 1 & 2x + 3y = 20 & \\ x + y = 8 & \times 2 & 2x + 2y = 16 & - \\ \hline & & y = 4 & \end{array} $
pers(i) : $ x + y = 8 \rightarrow x + 4 = 8 \rightarrow x = 4 $.
titik potongnya : (4,4)
Gambar DHP nya :
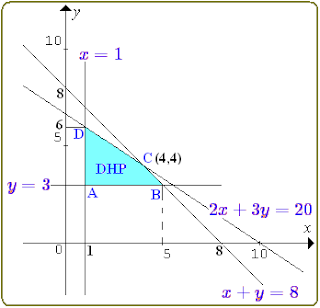
*). Susbstitusi $ x = 1 \, $ ke persamaan $ 2x + 3y = 20 \, $ :
$ 2x + 3y = 20 \rightarrow 2.1 + 3y = 20 \rightarrow 2 + 3y = 20 \rightarrow y = 6 $
Sehingga diperoleh titik D(1,6)
*). Susbstitusi $ y=3 \, $ ke persamaan $ x + y = 8 \, $ :
$ x + y = 8 \rightarrow x + 3 = 8 \rightarrow x = 5 $
Sehingga diperoleh titik B(5,3)
$\clubsuit \,$ Substitusi semua titik pojok ke fungsi tujuan : $ f(x,y) = 3x + 2y $
$\begin{align} A(1,3) \rightarrow f(1,3) & = 3.1 + 2.3 = 9 \\ B(5,3) \rightarrow f(5,3) & = 3.5 + 2.3 = 21 \\ C(4,4) \rightarrow f(4,4) & = 3.4 + 2.4 = 20 \\ D(1,6) \rightarrow f(1,6) & = 3.1 + 2.6 = 15 \end{align} $
Jadi, nilai minimumnya adalah 9. $ \heartsuit $
*). Gambar garis kedua persamaan :
$ x + y = 8 \rightarrow (0,8) , \, (8,0) $
$ 2x + 3y = 20 \rightarrow (0,\frac{20}{3}) , \, (10,0) $
garis $ x = 1 \, $ adalah garis tegak.
garis $ y = 3 \, $ adalah garis mendatar.
*). Titik potong kedua garis, eliminasi kedua persamaan :
$ \begin{array}{c|c|cc} 2x + 3y = 20 & \times 1 & 2x + 3y = 20 & \\ x + y = 8 & \times 2 & 2x + 2y = 16 & - \\ \hline & & y = 4 & \end{array} $
pers(i) : $ x + y = 8 \rightarrow x + 4 = 8 \rightarrow x = 4 $.
titik potongnya : (4,4)
Gambar DHP nya :

*). Susbstitusi $ x = 1 \, $ ke persamaan $ 2x + 3y = 20 \, $ :
$ 2x + 3y = 20 \rightarrow 2.1 + 3y = 20 \rightarrow 2 + 3y = 20 \rightarrow y = 6 $
Sehingga diperoleh titik D(1,6)
*). Susbstitusi $ y=3 \, $ ke persamaan $ x + y = 8 \, $ :
$ x + y = 8 \rightarrow x + 3 = 8 \rightarrow x = 5 $
Sehingga diperoleh titik B(5,3)
$\clubsuit \,$ Substitusi semua titik pojok ke fungsi tujuan : $ f(x,y) = 3x + 2y $
$\begin{align} A(1,3) \rightarrow f(1,3) & = 3.1 + 2.3 = 9 \\ B(5,3) \rightarrow f(5,3) & = 3.5 + 2.3 = 21 \\ C(4,4) \rightarrow f(4,4) & = 3.4 + 2.4 = 20 \\ D(1,6) \rightarrow f(1,6) & = 3.1 + 2.6 = 15 \end{align} $
Jadi, nilai minimumnya adalah 9. $ \heartsuit $