Nomor 21
Nilai $x \, $ yang memenuhi pertidaksamaan $\frac{x^2-4x+4}{x^2+x-12} \leq 0 \, $ adalah ....
$\spadesuit \, $ Menyelesaikan pertidaksamaan
$\begin{align} \frac{x^2-4x+4}{x^2+x-12} \leq 0 \\ \frac{(x-2)^2}{(x-3)(x+4)} \leq 0 \\ x=2, \, x= 3, \, x = -4 \end{align}$
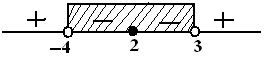
Jadi, solusinya adalah $ HP = \{ -4 < x < 3 \} . \heartsuit $
$\begin{align} \frac{x^2-4x+4}{x^2+x-12} \leq 0 \\ \frac{(x-2)^2}{(x-3)(x+4)} \leq 0 \\ x=2, \, x= 3, \, x = -4 \end{align}$

Jadi, solusinya adalah $ HP = \{ -4 < x < 3 \} . \heartsuit $
Nomor 22
Nilai maksimum dari $20x+8 \, $ untuk $x \, $ dan $y \, $ yang memenuhi $x+y \geq 20 , \, 0 \leq x \leq 20 \, $ dan $ 0 \leq y \leq 48 \, $
adalah ....
$\clubsuit \, $ Gambar
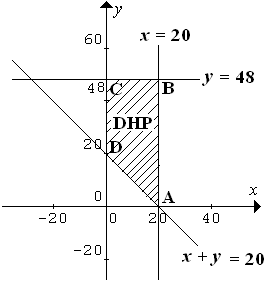
$\clubsuit \, $ Substitusi semua titik pojok ke fungsi tujuan : $z = 20x+8 $
$A(20,0) \rightarrow z=20.20 + 8 = 408 $
$B(20,48) \rightarrow z=20.20 + 8 = 408 $
$C(0,48) \rightarrow z=20.0 + 8 = 8 $
$D(0,20) \rightarrow z=20.0 + 8 = 8 $
Jadi, nilai maksimumnya adalah 408. $ \heartsuit $

$\clubsuit \, $ Substitusi semua titik pojok ke fungsi tujuan : $z = 20x+8 $
$A(20,0) \rightarrow z=20.20 + 8 = 408 $
$B(20,48) \rightarrow z=20.20 + 8 = 408 $
$C(0,48) \rightarrow z=20.0 + 8 = 8 $
$D(0,20) \rightarrow z=20.0 + 8 = 8 $
Jadi, nilai maksimumnya adalah 408. $ \heartsuit $
Nomor 23
Jika sudut $\theta \, $ di kuadran IV dan $\cos \theta = \frac{1}{a} \, $ , maka $\sin \theta = .... $
$\spadesuit \, \theta \, \, $ dikuadran IV artinya nilai $\cos \, $ positif, sehingga untuk $\cos \theta = \frac{1}{a} \, $
, maka nilai $ a > 0 \, $ (positif)

$\spadesuit \, $ Nilai $\sin \theta \, $ negatif karena di kuadran IV
$ \sin \theta = -\frac{\sqrt{a^2-1}}{a} $
Jadi, nilai $ \sin \theta = -\frac{\sqrt{a^2-1}}{a} . \heartsuit $

$\spadesuit \, $ Nilai $\sin \theta \, $ negatif karena di kuadran IV
$ \sin \theta = -\frac{\sqrt{a^2-1}}{a} $
Jadi, nilai $ \sin \theta = -\frac{\sqrt{a^2-1}}{a} . \heartsuit $
Nomor 24
Bilangan bulat terkecil $n \, $ yang memenuhi $n \cos \frac{1}{6} \pi > 30 \, $ adalah ....
$\clubsuit \,$ Menentukan nilai $n$
$\begin{align} n \cos \frac{1}{6} \pi & > 30 \\ n \cos 30^\circ & > 30 \\ n . \frac{1}{2} \sqrt{3} & > 30 \\ n & > \frac{30}{\sqrt{3}} . 2 \\ n & > 20\sqrt{3} \\ n & > 34,64 \end{align}$
Jadi, nilai $n \, $ bulat terkecil adalah 35. $ \heartsuit $
$\begin{align} n \cos \frac{1}{6} \pi & > 30 \\ n \cos 30^\circ & > 30 \\ n . \frac{1}{2} \sqrt{3} & > 30 \\ n & > \frac{30}{\sqrt{3}} . 2 \\ n & > 20\sqrt{3} \\ n & > 34,64 \end{align}$
Jadi, nilai $n \, $ bulat terkecil adalah 35. $ \heartsuit $
Nomor 25
$\displaystyle \lim_{x \to 0} \frac{-x+ \tan x }{x} = .... $
$\spadesuit \, $ Menentukan nilai limitnya
$\begin{align} \displaystyle \lim_{x \to 0} \frac{-x+ \tan x }{x} & = \displaystyle \lim_{x \to 0} \frac{-x }{x} + \frac{ \tan x }{x} \\ & = \displaystyle \lim_{x \to 0} -1 + \frac{ \tan x }{x} \\ & = -1 + \frac{1}{1} = -1 + 1 = 0 \end{align}$
Jadi, nilai limitnya adalah 0. $ \heartsuit $
$\begin{align} \displaystyle \lim_{x \to 0} \frac{-x+ \tan x }{x} & = \displaystyle \lim_{x \to 0} \frac{-x }{x} + \frac{ \tan x }{x} \\ & = \displaystyle \lim_{x \to 0} -1 + \frac{ \tan x }{x} \\ & = -1 + \frac{1}{1} = -1 + 1 = 0 \end{align}$
Jadi, nilai limitnya adalah 0. $ \heartsuit $



