Nomor 11
Fungsi $ f(x) = \sqrt{\sin ^2 x + \frac{x}{2} + \pi}, \, -\pi < x < 2\pi \, $ turun pada interval ....
$\clubsuit \, $ Konsep dasar
*). fungsi $ f(x) \, $ turun, syaratnya : $ f^\prime (x) < 0 $
*). turunan : $ y = \sqrt{x} \rightarrow y^\prime = \frac{f^\prime (x) }{2 \sqrt{x} } $
*). Persamaan trigonometri : $ \sin f(x) = \sin \theta $
Solusinya : $ f(x) = \theta + k2\pi \, $ dan $ f(x) = (180^\circ - \theta ) + k2\pi $
dengan $ k \, $ bilangan bulat dan $ \pi = 180^\circ $
$\clubsuit \, $ Menenentukan turunan fungsinya
$\begin{align} f(x) & = \sqrt{\sin ^2 x + \frac{x}{2} + \pi} \\ f^\prime (x) & = \frac{\text{turunan dari } \, (\sin ^2 x + \frac{x}{2} + \pi ) }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \\ & = \frac{ 2 \sin x \cos x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \\ & = \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \end{align}$
Untuk interval $ -\pi < x < 2\pi , \, $ maka nilai $ \sin ^2 x + \frac{x}{2} + \pi \, $ selalu positif.
$\clubsuit \, $ Syarat fungsi turun
$\begin{align} f^\prime (x) & < 0 \\ \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} & < 0 \end{align}$
Karena nilai $ \sin ^2 x + \frac{x}{2} + \pi \, $ selalu positif pada interval $ -\pi < x < 2\pi , \, $ maka agar $ \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} < 0 \, $ haruslah $ \sin 2x + \frac{1}{2} < 0 \, $ (negatif).
$\clubsuit \, $ Menentukan akar-akar dari $ \sin 2x + \frac{1}{2} < 0 $
$\begin{align} \sin 2x + \frac{1}{2} & = 0 \\ \sin 2x & = - \frac{1}{2} \\ \sin 2x & = \sin 210^\circ \\ f(x) & = 2x , \, \theta = 210^\circ \end{align}$
*). Solusinya : $ f(x) = \theta + k2\pi $
$ 2x = 210^\circ + k2\pi \rightarrow x = 105^\circ + k \pi $
$ k = -1 \rightarrow x = 105^\circ + -1 . \pi = -75^\circ = \frac{-5\pi}{12} $
$ k = 0 \rightarrow x = 105^\circ + 0 . \pi = 105^\circ = \frac{7\pi}{12} $
$ k = 1 \rightarrow x = 105^\circ + 1 . \pi = 285^\circ = \frac{19\pi}{12} $
*). Solusinya : $ f(x) = (180^\circ - \theta ) + k2\pi $
$ 2x = ( 180^\circ - 210^\circ ) + k2\pi \rightarrow x = -15^\circ + k \pi $
$ k = 0 \rightarrow x = -15^\circ + 0. \pi = -15^\circ = \frac{-\pi}{12} $
$ k = 1 \rightarrow x = -15^\circ + 1. \pi = 165^\circ = \frac{11\pi}{12} $
$ k = 2 \rightarrow x = -15^\circ + 2. \pi = 345^\circ = \frac{23\pi}{12} $
*). Garis bilangannya :
Pertidaksamaannya : $ \sin 2x + \frac{1}{2} < 0 \, $
Yang diasrsir daerah negatif karena yang diminta kurang dari ($ < $ ).

Berdasarkan pilihannya, maka solusinya adalah $ 105^\circ < x < 165^\circ \, $ atau dapat ditulis $ \frac{7\pi}{12} < x < \frac{11\pi}{12} $ .
Jadi, fungsi $ f(x) $ turun pada interval $ \frac{7\pi}{12} < x < \frac{11\pi}{12} . \, \heartsuit $
*). fungsi $ f(x) \, $ turun, syaratnya : $ f^\prime (x) < 0 $
*). turunan : $ y = \sqrt{x} \rightarrow y^\prime = \frac{f^\prime (x) }{2 \sqrt{x} } $
*). Persamaan trigonometri : $ \sin f(x) = \sin \theta $
Solusinya : $ f(x) = \theta + k2\pi \, $ dan $ f(x) = (180^\circ - \theta ) + k2\pi $
dengan $ k \, $ bilangan bulat dan $ \pi = 180^\circ $
$\clubsuit \, $ Menenentukan turunan fungsinya
$\begin{align} f(x) & = \sqrt{\sin ^2 x + \frac{x}{2} + \pi} \\ f^\prime (x) & = \frac{\text{turunan dari } \, (\sin ^2 x + \frac{x}{2} + \pi ) }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \\ & = \frac{ 2 \sin x \cos x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \\ & = \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} \end{align}$
Untuk interval $ -\pi < x < 2\pi , \, $ maka nilai $ \sin ^2 x + \frac{x}{2} + \pi \, $ selalu positif.
$\clubsuit \, $ Syarat fungsi turun
$\begin{align} f^\prime (x) & < 0 \\ \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} & < 0 \end{align}$
Karena nilai $ \sin ^2 x + \frac{x}{2} + \pi \, $ selalu positif pada interval $ -\pi < x < 2\pi , \, $ maka agar $ \frac{ \sin 2x + \frac{1}{2} }{2\sqrt{\sin ^2 x + \frac{x}{2} + \pi}} < 0 \, $ haruslah $ \sin 2x + \frac{1}{2} < 0 \, $ (negatif).
$\clubsuit \, $ Menentukan akar-akar dari $ \sin 2x + \frac{1}{2} < 0 $
$\begin{align} \sin 2x + \frac{1}{2} & = 0 \\ \sin 2x & = - \frac{1}{2} \\ \sin 2x & = \sin 210^\circ \\ f(x) & = 2x , \, \theta = 210^\circ \end{align}$
*). Solusinya : $ f(x) = \theta + k2\pi $
$ 2x = 210^\circ + k2\pi \rightarrow x = 105^\circ + k \pi $
$ k = -1 \rightarrow x = 105^\circ + -1 . \pi = -75^\circ = \frac{-5\pi}{12} $
$ k = 0 \rightarrow x = 105^\circ + 0 . \pi = 105^\circ = \frac{7\pi}{12} $
$ k = 1 \rightarrow x = 105^\circ + 1 . \pi = 285^\circ = \frac{19\pi}{12} $
*). Solusinya : $ f(x) = (180^\circ - \theta ) + k2\pi $
$ 2x = ( 180^\circ - 210^\circ ) + k2\pi \rightarrow x = -15^\circ + k \pi $
$ k = 0 \rightarrow x = -15^\circ + 0. \pi = -15^\circ = \frac{-\pi}{12} $
$ k = 1 \rightarrow x = -15^\circ + 1. \pi = 165^\circ = \frac{11\pi}{12} $
$ k = 2 \rightarrow x = -15^\circ + 2. \pi = 345^\circ = \frac{23\pi}{12} $
*). Garis bilangannya :
Pertidaksamaannya : $ \sin 2x + \frac{1}{2} < 0 \, $
Yang diasrsir daerah negatif karena yang diminta kurang dari ($ < $ ).

Berdasarkan pilihannya, maka solusinya adalah $ 105^\circ < x < 165^\circ \, $ atau dapat ditulis $ \frac{7\pi}{12} < x < \frac{11\pi}{12} $ .
Jadi, fungsi $ f(x) $ turun pada interval $ \frac{7\pi}{12} < x < \frac{11\pi}{12} . \, \heartsuit $
Nomor 12
Pada interval $ -2 \leq x \leq 2 , \, $ luas daerah di bawah kurva $ y = 4 - x^2 \, $ dan di atas garis $ y = k \, $ sama dengan luas
daearah di atas kurva $ y = 4 - x^2 \, $ dan di bawah garis $ y = k. \, $ Nilai $ k = .... $
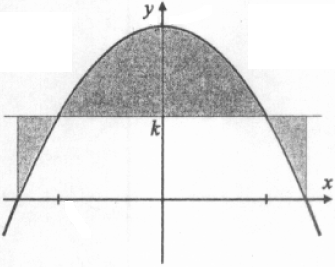

$\spadesuit \, $ Gambarnya

Misalkan perpotongan $ y = k \, $ dan $ y = 4 - x^2 \, $ di $ x = -a \, $ dan $ x = a $ .
$\spadesuit \, $ Menentukan Luas daerah di atas (LI) garis $ y = k $ dan di bawah (LII)
$\begin{align} LI(A) & = \int \limits_{-a}^a \text{(grafik atas)} - \text{(grafik bawah)} dx \\ & = \int \limits_{-a}^a (4-x^2) - (k) dx \\ & = \int \limits_{-a}^a (4-k) - x^2 dx \\ & = [(4-k)x - \frac{1}{3}x^3] _{-a}^{a} \\ & = [(4-k)a - \frac{1}{3}a^3] - [(4-k)(-a) - \frac{1}{3}(-a)^3] \\ & = 2 [(4-k)a - \frac{1}{3}a^3] \\ LII(2B) & = 2 \int \limits_{a}^2 \text{(grafik atas)} - \text{(grafik bawah)} dx \\ & = 2 \int \limits_{a}^2 (k) - (4-x^2) dx \\ & = 2 \int \limits_{a}^2 (k-4) +x^2 dx \\ & = 2 [ (k-4)x + \frac{1}{3}x^3]_a^2 \\ & = 2 ([ (k-4).2 + \frac{1}{3}2^3]- [ (k-4).a + \frac{1}{3}a^3]) \\ & = 2 [ (k-4).2 + \frac{1}{3}2^3]+ 2[ (4-k).a - \frac{1}{3}a^3] \\ & = 2 [ (k-4).2 + \frac{8}{3}]+ 2[ (4-k).a - \frac{1}{3}a^3] \end{align}$
$\spadesuit \, $ Menentukan Nilai $ k $
$\begin{align} LI(A) & = LII(2B) \\ 2 [(4-k)a - \frac{1}{3}a^3] & = 2 [ (k-4).2 + \frac{8}{3}]+ 2[ (4-k).a - \frac{1}{3}a^3] \\ 0 & = 2 [ (k-4).2 + \frac{8}{3}] \\ [ (k-4).2 + \frac{8}{3}] & = 0 \\ 2k - 8 + + \frac{8}{3} & = 0 \\ 2k & = \frac{16}{3} \\ k & = \frac{8}{3} \end{align}$
Jadi, nilai $ k = \frac{8}{3} . \, \heartsuit $

Misalkan perpotongan $ y = k \, $ dan $ y = 4 - x^2 \, $ di $ x = -a \, $ dan $ x = a $ .
$\spadesuit \, $ Menentukan Luas daerah di atas (LI) garis $ y = k $ dan di bawah (LII)
$\begin{align} LI(A) & = \int \limits_{-a}^a \text{(grafik atas)} - \text{(grafik bawah)} dx \\ & = \int \limits_{-a}^a (4-x^2) - (k) dx \\ & = \int \limits_{-a}^a (4-k) - x^2 dx \\ & = [(4-k)x - \frac{1}{3}x^3] _{-a}^{a} \\ & = [(4-k)a - \frac{1}{3}a^3] - [(4-k)(-a) - \frac{1}{3}(-a)^3] \\ & = 2 [(4-k)a - \frac{1}{3}a^3] \\ LII(2B) & = 2 \int \limits_{a}^2 \text{(grafik atas)} - \text{(grafik bawah)} dx \\ & = 2 \int \limits_{a}^2 (k) - (4-x^2) dx \\ & = 2 \int \limits_{a}^2 (k-4) +x^2 dx \\ & = 2 [ (k-4)x + \frac{1}{3}x^3]_a^2 \\ & = 2 ([ (k-4).2 + \frac{1}{3}2^3]- [ (k-4).a + \frac{1}{3}a^3]) \\ & = 2 [ (k-4).2 + \frac{1}{3}2^3]+ 2[ (4-k).a - \frac{1}{3}a^3] \\ & = 2 [ (k-4).2 + \frac{8}{3}]+ 2[ (4-k).a - \frac{1}{3}a^3] \end{align}$
$\spadesuit \, $ Menentukan Nilai $ k $
$\begin{align} LI(A) & = LII(2B) \\ 2 [(4-k)a - \frac{1}{3}a^3] & = 2 [ (k-4).2 + \frac{8}{3}]+ 2[ (4-k).a - \frac{1}{3}a^3] \\ 0 & = 2 [ (k-4).2 + \frac{8}{3}] \\ [ (k-4).2 + \frac{8}{3}] & = 0 \\ 2k - 8 + + \frac{8}{3} & = 0 \\ 2k & = \frac{16}{3} \\ k & = \frac{8}{3} \end{align}$
Jadi, nilai $ k = \frac{8}{3} . \, \heartsuit $
Nomor 13
Banyak kurva $ Ax^2 + \left( \frac{By}{2} \right)^2 = 0 \, $ dengan $ A \, $ dan $ B \, $ dua bilangan berbeda yang dipilih dari
$ \{-1,0,1,2,4\} \, $ adalah ....
$\spadesuit \, $ Untuk menyelesaikan soalnya, kita harus langsung mencoba nilai A dan B yang berbeda yang dipilih dari
{-1, 0, 1, 2, 4} , dan kita substitusi ke persamaan $ Ax^2 + \left( \frac{By}{2} \right)^2 = 0, \, $
seperti di bawah ini.
$\begin{align} Ax^2 + \left( \frac{By}{2} \right)^2 & = 0 \\ A = 0 \rightarrow \left( \frac{By}{2} \right)^2 & = 0 \rightarrow y^2 = 0 \, \, \, \, \text{(1 kurva)} \\ B = 0 \rightarrow Ax^2 & = 0 \rightarrow x^2 = 0 \, \, \, \, \text{(1 kurva)} \\ A = -1 \rightarrow -x^2 + \left( \frac{1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ -x^2 + \left( \frac{2}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ -x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 1 \rightarrow x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ x^2 + \left( \frac{2}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 2 \rightarrow 2x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ 2x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 4 \rightarrow 4x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \end{align}$
Jadi, total ada 11 kurva yang berbeda.
$\begin{align} Ax^2 + \left( \frac{By}{2} \right)^2 & = 0 \\ A = 0 \rightarrow \left( \frac{By}{2} \right)^2 & = 0 \rightarrow y^2 = 0 \, \, \, \, \text{(1 kurva)} \\ B = 0 \rightarrow Ax^2 & = 0 \rightarrow x^2 = 0 \, \, \, \, \text{(1 kurva)} \\ A = -1 \rightarrow -x^2 + \left( \frac{1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ -x^2 + \left( \frac{2}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ -x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 1 \rightarrow x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ x^2 + \left( \frac{2}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 2 \rightarrow 2x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ 2x^2 + \left( \frac{4}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \\ A = 4 \rightarrow 4x^2 + \left( \frac{-1}{2} y \right)^2 & = 0 \, \, \, \, \text{(1 kurva)} \end{align}$
Jadi, total ada 11 kurva yang berbeda.
Nomor 14
Tiga kelas masing-masing terdiri atas 30 siswa. Satu kelas diantaranya terdiri atas laki-laki saja. Satu siswa dipilih dari tiap-tiap kelas.
Peluang terpilih ketiganya laki-laki adalah 7/36. Peluang terpilih dua laki-laki dan satu perempuan adalah ....
$\spadesuit \, $ Konsep peluang komplemen : $ P(A^c) = 1 - P(A) $
$\spadesuit \, $ Satu kelas terdiri dari laki-laki dan perempuan, artinya berlaku peluang komplemen yaitu peluang perempuan kebalikan dari peluang laki-laki atau sebaliknya, sehingga bisa ditulis $ P(P) = 1 - P(L) $ .
$\spadesuit \, $ Ada tiga kelas, misalnya kelas I ada $P_1 \, $ dan $ L_1 \, $ , kelas II ada $P_2 \, $ dan $ L_2 \, $ dan kelas III hanya ada $ L_3 \, $ saja. $ P_1 \, $ artinya perempuan pada kelas I yang terpilih, begitu juga simbol $ L_1, \, P_2, \, L_2, \, L_3 $ . Karena kelas III hanya ada laki-laki saja, maka peluangnya 1 atau ditulis $ P(L_3) = 1 $.
$\spadesuit \, $ Menentukan peluang masing-masing dengan setiap kelas dipilih satu siswa.
peluang terpilihnya laki-laki semua adalah $ \frac{7}{36} $
$\begin{align} P(L_1).P(L_2).P(L_3) & = \frac{7}{36} \\ P(L_1).P(L_2).1 & = \frac{7}{6 . 6} . \frac{5}{5} \\ P(L_1).P(L_2) & = \frac{7}{30} . \frac{5}{6} \end{align}$
artinya $ P(L_1) = \frac{7}{30} , \, $ dan $ P(L_2) = \frac{5}{6} $
$\spadesuit \, $ Menentukan peluang masing-masing dengan peluang komplemen
$ P(L_1) = \frac{7}{30} \rightarrow P(P_1) = 1 - P(L_1) = 1 - \frac{7}{30} = \frac{23}{30} $
$ P(L_2) = \frac{5}{6} \rightarrow P(P_2) = 1 - P(L_2) = 1 - \frac{5}{6} = \frac{1}{6} $
$ P(L_3) = 1 $
$\spadesuit \, $ Peluang dua laki-laki (2L) dan satu perempuan (1P)
$\begin{align} & P(P_1).P(L_2).P(L_3) + P(P_2).P(L_1).P(L_3) \\ & = \frac{23}{30}. \frac{5}{6}. 1 + \frac{1}{6}. \frac{7}{30}. 1 \\ & = \frac{115}{180} + \frac{7}{180} \\ & = \frac{122}{180} = \frac{61}{90} \end{align}$
Jadi, peluang terpilihnya 2L dan 1P adalah $ \frac{61}{90}. \, \heartsuit $
$\spadesuit \, $ Satu kelas terdiri dari laki-laki dan perempuan, artinya berlaku peluang komplemen yaitu peluang perempuan kebalikan dari peluang laki-laki atau sebaliknya, sehingga bisa ditulis $ P(P) = 1 - P(L) $ .
$\spadesuit \, $ Ada tiga kelas, misalnya kelas I ada $P_1 \, $ dan $ L_1 \, $ , kelas II ada $P_2 \, $ dan $ L_2 \, $ dan kelas III hanya ada $ L_3 \, $ saja. $ P_1 \, $ artinya perempuan pada kelas I yang terpilih, begitu juga simbol $ L_1, \, P_2, \, L_2, \, L_3 $ . Karena kelas III hanya ada laki-laki saja, maka peluangnya 1 atau ditulis $ P(L_3) = 1 $.
$\spadesuit \, $ Menentukan peluang masing-masing dengan setiap kelas dipilih satu siswa.
peluang terpilihnya laki-laki semua adalah $ \frac{7}{36} $
$\begin{align} P(L_1).P(L_2).P(L_3) & = \frac{7}{36} \\ P(L_1).P(L_2).1 & = \frac{7}{6 . 6} . \frac{5}{5} \\ P(L_1).P(L_2) & = \frac{7}{30} . \frac{5}{6} \end{align}$
artinya $ P(L_1) = \frac{7}{30} , \, $ dan $ P(L_2) = \frac{5}{6} $
$\spadesuit \, $ Menentukan peluang masing-masing dengan peluang komplemen
$ P(L_1) = \frac{7}{30} \rightarrow P(P_1) = 1 - P(L_1) = 1 - \frac{7}{30} = \frac{23}{30} $
$ P(L_2) = \frac{5}{6} \rightarrow P(P_2) = 1 - P(L_2) = 1 - \frac{5}{6} = \frac{1}{6} $
$ P(L_3) = 1 $
$\spadesuit \, $ Peluang dua laki-laki (2L) dan satu perempuan (1P)
$\begin{align} & P(P_1).P(L_2).P(L_3) + P(P_2).P(L_1).P(L_3) \\ & = \frac{23}{30}. \frac{5}{6}. 1 + \frac{1}{6}. \frac{7}{30}. 1 \\ & = \frac{115}{180} + \frac{7}{180} \\ & = \frac{122}{180} = \frac{61}{90} \end{align}$
Jadi, peluang terpilihnya 2L dan 1P adalah $ \frac{61}{90}. \, \heartsuit $
Nomor 15
Diketahui deret geometri takhingga mempunyai jumlah sama dengan nilai maksimum fungsi $ f(x) = -\frac{2}{3}x^3 + 2x + \frac{2}{3} \, $
untuk $ -1 \leq x \leq 2. \, $ Selisih suku kedua dan suku pertama deret geometri tersebut adalah $ -2f^\prime (0). \, $
Rasio deret geometri tersebut adalah ....
$\clubsuit \, $ Konsep dasar
*). Barisan geometri : $ u_n = ar^{n-1} $
*). Jumlah tak hingga : $ s_\infty = \frac{a}{1-r} $
*). Syarat stasioner (nilai maksimum/minimum) : $ f^\prime (x) = 0 $
$\clubsuit \, $ Menentukan turunan fungsi $ f(x) $
$\begin{align} f(x) & = -\frac{2}{3}x^3 + 2x + \frac{2}{3} \\ f^\prime (x) & = -2x^2 + 2 \\ f^\prime (0) & = -2.0^2 + 2 = 2 \end{align}$
$\clubsuit \, $ Menentukan nilai maksimum fungsi $ f(x) $
$\begin{align} \text{syarat : } f^\prime (x) & = 0 \\ -2x^2 + 2 & = 0 \\ x^2 & = 1 \\ x & = \pm \sqrt{1} = \pm 1 \end{align}$
nilai $ x \, $ pada interval $ -1 \leq x \leq 2 $
*). Uji semua nilai $ x \, $ yang diperoleh dari syarat stasioner dan intervalnya ke fungsi $ f(x) = -\frac{2}{3}x^3 + 2x + \frac{2}{3} $
$\begin{align} x = -1 \rightarrow f(-1) & = -\frac{2}{3}(-1)^3 + 2.(-1) + \frac{2}{3} = -\frac{2}{3} \\ x = 1 \rightarrow f(1) & = -\frac{2}{3}(1)^3 + 2.(1) + \frac{2}{3} = 2 \\ x = 2 \rightarrow f(2) & = -\frac{2}{3}(2)^3 + 2.(2) + \frac{2}{3} = -\frac{2}{3} \end{align}$
Artinya, nilai maksimum fungsi $ f(x) \, $ adalah 2 pada saat $ x = 1 $
$\clubsuit \, $ Menyusun persamaan
*). Jumlah tak hingga = nilai maksimum
$\begin{align} s_\infty & = 2 \\ \frac{a}{1-r} & = 2 \\ a & = 2(1-r) \, \, \, \, \, \text{...pers(i)} \end{align}$
*). Selisih $ u_2 \, $ dan $ u_1 \, $ = $ -2 f^\prime (0) $
$\begin{align} u_2 - u_1 & = -2 f^\prime (0) \\ ar - a & = -2 . 2 \\ a(r-1) & = -4 \, \, \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$\begin{align} a(r-1) & = -4 \\ 2(1-r)(r-1) & = -4 \, \, \, \, \, \text{(bagi -2)} \\ (r-1)(r-1) & = 2 \\ r^2 - 2r + 1 & = 2 \\ r^2 - 2r - 1 & = 0 \\ a = 1, \, b = -2, \, c & = -1 \\ r & = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a} \, \, \, \, \, \text{(Rumus ABC)} \\ r & = \frac{-(-2) \pm \sqrt{(-2)^2 - 4.1.(-1)}}{2.1} \\ r & = \frac{2 \pm \sqrt{8}}{2} \\ r & = \frac{2 \pm 2\sqrt{2}}{2} \\ r & = 1 \pm \sqrt{2} \end{align}$
Jadi, nilai rasionya $ r = 1 - \sqrt{2}. \, \heartsuit $
*). Barisan geometri : $ u_n = ar^{n-1} $
*). Jumlah tak hingga : $ s_\infty = \frac{a}{1-r} $
*). Syarat stasioner (nilai maksimum/minimum) : $ f^\prime (x) = 0 $
$\clubsuit \, $ Menentukan turunan fungsi $ f(x) $
$\begin{align} f(x) & = -\frac{2}{3}x^3 + 2x + \frac{2}{3} \\ f^\prime (x) & = -2x^2 + 2 \\ f^\prime (0) & = -2.0^2 + 2 = 2 \end{align}$
$\clubsuit \, $ Menentukan nilai maksimum fungsi $ f(x) $
$\begin{align} \text{syarat : } f^\prime (x) & = 0 \\ -2x^2 + 2 & = 0 \\ x^2 & = 1 \\ x & = \pm \sqrt{1} = \pm 1 \end{align}$
nilai $ x \, $ pada interval $ -1 \leq x \leq 2 $
*). Uji semua nilai $ x \, $ yang diperoleh dari syarat stasioner dan intervalnya ke fungsi $ f(x) = -\frac{2}{3}x^3 + 2x + \frac{2}{3} $
$\begin{align} x = -1 \rightarrow f(-1) & = -\frac{2}{3}(-1)^3 + 2.(-1) + \frac{2}{3} = -\frac{2}{3} \\ x = 1 \rightarrow f(1) & = -\frac{2}{3}(1)^3 + 2.(1) + \frac{2}{3} = 2 \\ x = 2 \rightarrow f(2) & = -\frac{2}{3}(2)^3 + 2.(2) + \frac{2}{3} = -\frac{2}{3} \end{align}$
Artinya, nilai maksimum fungsi $ f(x) \, $ adalah 2 pada saat $ x = 1 $
$\clubsuit \, $ Menyusun persamaan
*). Jumlah tak hingga = nilai maksimum
$\begin{align} s_\infty & = 2 \\ \frac{a}{1-r} & = 2 \\ a & = 2(1-r) \, \, \, \, \, \text{...pers(i)} \end{align}$
*). Selisih $ u_2 \, $ dan $ u_1 \, $ = $ -2 f^\prime (0) $
$\begin{align} u_2 - u_1 & = -2 f^\prime (0) \\ ar - a & = -2 . 2 \\ a(r-1) & = -4 \, \, \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \, $ Substitusi pers(i) ke pers(ii)
$\begin{align} a(r-1) & = -4 \\ 2(1-r)(r-1) & = -4 \, \, \, \, \, \text{(bagi -2)} \\ (r-1)(r-1) & = 2 \\ r^2 - 2r + 1 & = 2 \\ r^2 - 2r - 1 & = 0 \\ a = 1, \, b = -2, \, c & = -1 \\ r & = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a} \, \, \, \, \, \text{(Rumus ABC)} \\ r & = \frac{-(-2) \pm \sqrt{(-2)^2 - 4.1.(-1)}}{2.1} \\ r & = \frac{2 \pm \sqrt{8}}{2} \\ r & = \frac{2 \pm 2\sqrt{2}}{2} \\ r & = 1 \pm \sqrt{2} \end{align}$
Jadi, nilai rasionya $ r = 1 - \sqrt{2}. \, \heartsuit $