Nomor 11
Nilai $ \cos \frac{2\pi}{7} + \cos \frac{4\pi}{7} + \cos \frac{6\pi}{7} = .... $
$\clubsuit \, $ Konsep trigonometri : $ 2\cos x \sin y = \sin (x+y) - \sin ( x- y) $
$\clubsuit \, $ Menyelesaikan soal dengan permisalan : $ x = \frac{\pi}{7} $
Modifikasi soal dengan mengalikannya dengan $ \frac{2\sin x}{2\sin x} \, $ agar mengarah ke rumus dasar di atas.
$\begin{align} & \cos \frac{2\pi}{7} + \cos \frac{4\pi}{7} + \cos \frac{6\pi}{7} \\ & = \cos 2x + \cos 4x + \cos 6x \\ & = ( \cos 2x + \cos 4x + \cos 6x ) . \frac{2\sin x}{2\sin x} \\ & = \frac{ 2\cos 2x \sin x + 2\cos 4x .\sin x + 2\cos 6x . \sin x }{2\sin x} \\ & = \frac{ (\sin 3x - \sin x) + (\sin 5x - \sin 3x ) + (\sin 7x - \sin 5x) }{2\sin x} \\ & = \frac{ \sin 7x - \sin x }{2\sin x} \, \, \, \, \text{ (substitusi } x = \frac{\pi}{7} \, ) \\ & = \frac{ \sin 7. \frac{\pi}{7} - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ \sin \pi - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ 0 - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} \\ & = \frac{ - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ - 1 }{2} \end{align}$
Jadi, nilai $ \cos \frac{2\pi}{7} + \cos \frac{4\pi}{7} + \cos \frac{6\pi}{7} = - \frac{1}{2} . \heartsuit $
$\clubsuit \, $ Menyelesaikan soal dengan permisalan : $ x = \frac{\pi}{7} $
Modifikasi soal dengan mengalikannya dengan $ \frac{2\sin x}{2\sin x} \, $ agar mengarah ke rumus dasar di atas.
$\begin{align} & \cos \frac{2\pi}{7} + \cos \frac{4\pi}{7} + \cos \frac{6\pi}{7} \\ & = \cos 2x + \cos 4x + \cos 6x \\ & = ( \cos 2x + \cos 4x + \cos 6x ) . \frac{2\sin x}{2\sin x} \\ & = \frac{ 2\cos 2x \sin x + 2\cos 4x .\sin x + 2\cos 6x . \sin x }{2\sin x} \\ & = \frac{ (\sin 3x - \sin x) + (\sin 5x - \sin 3x ) + (\sin 7x - \sin 5x) }{2\sin x} \\ & = \frac{ \sin 7x - \sin x }{2\sin x} \, \, \, \, \text{ (substitusi } x = \frac{\pi}{7} \, ) \\ & = \frac{ \sin 7. \frac{\pi}{7} - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ \sin \pi - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ 0 - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} \\ & = \frac{ - \sin \frac{\pi}{7} }{2\sin \frac{\pi}{7}} = \frac{ - 1 }{2} \end{align}$
Jadi, nilai $ \cos \frac{2\pi}{7} + \cos \frac{4\pi}{7} + \cos \frac{6\pi}{7} = - \frac{1}{2} . \heartsuit $
Nomor 12
Jika $\displaystyle \lim_{x \to a} \left( f(x)+\frac{1}{g(x)} \right)=4$ dan $\displaystyle \lim_{x \to a} \left( f(x)- \frac{1}{g(x)} \right)=-3$,
maka $\displaystyle \lim_{x \to a} \left(f(x)g(x) \right)=...$
$\spadesuit \, $ Substitusi semua $x$ dengan $a$ pada masing-masing limit:
$\displaystyle \lim_{x \to a} \left( f(x)+\frac{1}{g(x)} \right)=4 \Rightarrow \left( f(a)+\frac{1}{g(a)} \right)=4$ ...pers(i)
$\displaystyle \lim_{x \to a} \left( f(x)- \frac{1}{g(x)} \right)=-3 \Rightarrow \left( f(a)- \frac{1}{g(a)} \right)=-3$ ...pers(ii)
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii), diperoleh : $f(a)=\frac{1}{2}, \, g(a)=\frac{2}{7}.$
$\spadesuit \, $ Substitusi nilai $f(a)$ dan $g(a)$
$\begin{align} \displaystyle \lim_{x \to a} \left( f(x)g(x) \right)&= \left( f(a)g(a) \right) \\ &= \frac{1}{2} \times \frac{2}{7} \\ &=\frac{2}{14} \end{align}$
Jadi, nilai $\displaystyle \lim_{x \to a} \left( f(x)g(x) \right)=\frac{2}{14}. \heartsuit$
$\displaystyle \lim_{x \to a} \left( f(x)+\frac{1}{g(x)} \right)=4 \Rightarrow \left( f(a)+\frac{1}{g(a)} \right)=4$ ...pers(i)
$\displaystyle \lim_{x \to a} \left( f(x)- \frac{1}{g(x)} \right)=-3 \Rightarrow \left( f(a)- \frac{1}{g(a)} \right)=-3$ ...pers(ii)
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii), diperoleh : $f(a)=\frac{1}{2}, \, g(a)=\frac{2}{7}.$
$\spadesuit \, $ Substitusi nilai $f(a)$ dan $g(a)$
$\begin{align} \displaystyle \lim_{x \to a} \left( f(x)g(x) \right)&= \left( f(a)g(a) \right) \\ &= \frac{1}{2} \times \frac{2}{7} \\ &=\frac{2}{14} \end{align}$
Jadi, nilai $\displaystyle \lim_{x \to a} \left( f(x)g(x) \right)=\frac{2}{14}. \heartsuit$
Nomor 13
Jika $ A = \left[ \begin{matrix} 1 & 0 \\ 2 & 1 \end{matrix} \right] , \, $ maka $ (I + A )^5 = .... $
$\spadesuit \, $ Konsep perpangkatan bentuk matriks tertentu
$ A = \left[ \begin{matrix} 1 & 0 \\ b & 1 \end{matrix} \right] \rightarrow A^n = \left[ \begin{matrix} 1 & 0 \\ b & 1 \end{matrix} \right]^n = \left[ \begin{matrix} 1 & 0 \\ b \times n & 1 \end{matrix} \right] $
matriks identitas : $ I = \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] $
$\spadesuit \, $ Menentukan hasil $ (I + A )^5 $
$\begin{align} (I + A )^5 & = \left( \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] + \left[ \begin{matrix} 1 & 0 \\ 2 & 1 \end{matrix} \right] \right)^5 \\ & = \left( \left[ \begin{matrix} 2 & 0 \\ 2 & 2 \end{matrix} \right] \right)^5 \\ & = \left( 2 \left[ \begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix} \right] \right)^5 \\ & = 2^5 \left( \begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix} \right)^5 \\ & = 32 \left( \begin{matrix} 1 & 0 \\ 1\times 5 & 1 \end{matrix} \right) \\ & = 32 \left( \begin{matrix} 1 & 0 \\ 5 & 1 \end{matrix} \right) \\ (I + A )^5 & = \left( \begin{matrix} 32 & 0 \\ 160 & 32 \end{matrix} \right) \end{align}$
Jadi, nilai $ (I + A )^5 = \left( \begin{matrix} 32 & 0 \\ 160 & 32 \end{matrix} \right) . \heartsuit $
$ A = \left[ \begin{matrix} 1 & 0 \\ b & 1 \end{matrix} \right] \rightarrow A^n = \left[ \begin{matrix} 1 & 0 \\ b & 1 \end{matrix} \right]^n = \left[ \begin{matrix} 1 & 0 \\ b \times n & 1 \end{matrix} \right] $
matriks identitas : $ I = \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] $
$\spadesuit \, $ Menentukan hasil $ (I + A )^5 $
$\begin{align} (I + A )^5 & = \left( \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] + \left[ \begin{matrix} 1 & 0 \\ 2 & 1 \end{matrix} \right] \right)^5 \\ & = \left( \left[ \begin{matrix} 2 & 0 \\ 2 & 2 \end{matrix} \right] \right)^5 \\ & = \left( 2 \left[ \begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix} \right] \right)^5 \\ & = 2^5 \left( \begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix} \right)^5 \\ & = 32 \left( \begin{matrix} 1 & 0 \\ 1\times 5 & 1 \end{matrix} \right) \\ & = 32 \left( \begin{matrix} 1 & 0 \\ 5 & 1 \end{matrix} \right) \\ (I + A )^5 & = \left( \begin{matrix} 32 & 0 \\ 160 & 32 \end{matrix} \right) \end{align}$
Jadi, nilai $ (I + A )^5 = \left( \begin{matrix} 32 & 0 \\ 160 & 32 \end{matrix} \right) . \heartsuit $
Nomor 14
Misalkan $A(t)$ menyatakan luas daerah di bawah kurva $y=bx^2 , 0\leq x \leq t$. Jika titik $P(x_0,0)$ sehingga $A(x_0):A(1)=1:8$, maka perbandingan
luas trapesium $ABPQ:DCPQ=...$


$\spadesuit \, $ Menentukan $A(t)$:
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
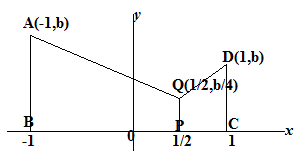
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
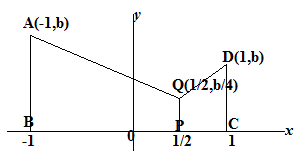
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
Nomor 15
Diberikan polinomial $ Q(x) \, $ dan $ f(x) = ax^3 + (a-b)x^2+2bx + a . \, $ Jika $ Q(x)f(x) \, $ dan $ Q(x) \, $ berturut-turut
memberikan sisa -26 dan 1 apabila masing-masing dibagi $ x -2 \, $ ,dan $ f(x) \, $ habis dibagi $ x -1 , \, $ maka $ f(x) \, $
dibagi $ x^2 + x \, $ memberikan sisa ....
$\spadesuit \, $ Teorema sisa : $\frac{f(x)}{x-a} \Rightarrow \text{sisa} = f(a)$
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
$ Q(x) : (x-2), \, $ sisa = 1 , artinya $ Q(2) = 1 \, $ ....pers(i)
$ Q(x)f(x) : (x-2), \, $ sisa = -26 , artinya $ Q(2)f(2) = -26 \, $ ....pers(ii)
$ f(x) : (x-1), \, $ sisa = 0 (karena habis dibagi) , artinya $ f(1) = 0 \, $ ....pers(iii)
Substitusi Pers(i) ke pers(ii) diperoleh $ f(2) = -26 \, $ ....pers(iv)
$\spadesuit \, $ Menentukan fungsi $ f(x) \, $ dengan $ f(1) = 0 \, $ dan $ f(2) = -26 $
$\begin{align} x=2 \rightarrow f(x) & = ax^3 + (a-b)x^2+2bx + a \\ f(2) & = a. 2^3 + (a-b).2^2+2b.2 + a \\ -26 & = 8a + 4a -4b + 4b + a \\ - 26 & = 13a \\ a & = -2 \\ x=1 \rightarrow f(x) & = ax^3 + (a-b)x^2+2bx + a \\ f(1) & = a. 1^3 + (a-b).1^2+2b.1 + a \\ 0 & = a + a -b + 2b + a \\ b & = -3a \\ b & = -3(-2) = 6 \end{align}$
Sehingga fungsinya :
$ f(x) = ax^3 + (a-b)x^2+2bx + a $
$ f(x) = -2x^3 + (-2-6)x^2 + 2.(6)x + (-2) $
$ f(x) = -2x^3 - 8x^2 + 12x - 2 $
$ f(0) = -2.0^3 - 8.0^2 + 12.0 - 2 \rightarrow f(0) = -2 $
$ f(-1) = -2.(-1)^3 - 8.(-1)^2 + 12.(-1) - 2 \rightarrow f(-1) = -20 $
$\spadesuit \, $ Menentukan sisa pembagian dengan substitusi nilai $ x $
$ f(x) \, $ dibagi $ x^2 + x = x(x+1) \, $ , misal sisanya $ S(x) = mx + n $
$\begin{align} x = 0 \rightarrow \text{ sisa } & = f(0) \\ m.0 + n & = -2 \\ n & = -2 \\ x = -1 \rightarrow \text{ sisa } & = f(-1) \\ m.(-1) + n & = -20 \\ -m + (-2) & = -20 \\ m & = 18 \end{align}$
Sehingga sisanya : $ S(x) = mx + n = 18x -2 $
Jadi, sisanya adalah $ 18x - 2 . \heartsuit$
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
$ Q(x) : (x-2), \, $ sisa = 1 , artinya $ Q(2) = 1 \, $ ....pers(i)
$ Q(x)f(x) : (x-2), \, $ sisa = -26 , artinya $ Q(2)f(2) = -26 \, $ ....pers(ii)
$ f(x) : (x-1), \, $ sisa = 0 (karena habis dibagi) , artinya $ f(1) = 0 \, $ ....pers(iii)
Substitusi Pers(i) ke pers(ii) diperoleh $ f(2) = -26 \, $ ....pers(iv)
$\spadesuit \, $ Menentukan fungsi $ f(x) \, $ dengan $ f(1) = 0 \, $ dan $ f(2) = -26 $
$\begin{align} x=2 \rightarrow f(x) & = ax^3 + (a-b)x^2+2bx + a \\ f(2) & = a. 2^3 + (a-b).2^2+2b.2 + a \\ -26 & = 8a + 4a -4b + 4b + a \\ - 26 & = 13a \\ a & = -2 \\ x=1 \rightarrow f(x) & = ax^3 + (a-b)x^2+2bx + a \\ f(1) & = a. 1^3 + (a-b).1^2+2b.1 + a \\ 0 & = a + a -b + 2b + a \\ b & = -3a \\ b & = -3(-2) = 6 \end{align}$
Sehingga fungsinya :
$ f(x) = ax^3 + (a-b)x^2+2bx + a $
$ f(x) = -2x^3 + (-2-6)x^2 + 2.(6)x + (-2) $
$ f(x) = -2x^3 - 8x^2 + 12x - 2 $
$ f(0) = -2.0^3 - 8.0^2 + 12.0 - 2 \rightarrow f(0) = -2 $
$ f(-1) = -2.(-1)^3 - 8.(-1)^2 + 12.(-1) - 2 \rightarrow f(-1) = -20 $
$\spadesuit \, $ Menentukan sisa pembagian dengan substitusi nilai $ x $
$ f(x) \, $ dibagi $ x^2 + x = x(x+1) \, $ , misal sisanya $ S(x) = mx + n $
$\begin{align} x = 0 \rightarrow \text{ sisa } & = f(0) \\ m.0 + n & = -2 \\ n & = -2 \\ x = -1 \rightarrow \text{ sisa } & = f(-1) \\ m.(-1) + n & = -20 \\ -m + (-2) & = -20 \\ m & = 18 \end{align}$
Sehingga sisanya : $ S(x) = mx + n = 18x -2 $
Jadi, sisanya adalah $ 18x - 2 . \heartsuit$