Nomor 6
Diketahui $ 4x^2 - 2mx + 2m - 3 = 0 \, $ supaya kedua akar - akarnya real berbeda dan positif haruslah .....
$\spadesuit \, $ PK : $ 4x^2 - 2mx + 2m - 3 = 0 $
$ \rightarrow a=4, b= -2m, c = 2m-3 $
$\spadesuit \, $ Syarat akar real beda positif
$ x_1+x_2 > 0, \, x_1.x_2 > 0 , \, D > 0 $
$\spadesuit \, $ Menyelesaikan syarat-syaratnya
*) $ x_1+x_2 > 0 \rightarrow \frac{-b}{a} > 0 \rightarrow \frac{-(-2m)}{4} > 0 \rightarrow m > 0 \, $ ....(HP1)
*) $ x_1.x_2 > 0 \rightarrow \frac{c}{a} > 0 \rightarrow \frac{2m-3}{4} > 0 \rightarrow m > \frac{3}{2} \, $ ....(HP2)
*) syarat $ D > 0 $
$\begin{align} D & > 0 \\ b^2-4ac & > 0 \\ (-2m)^2-4.4.(2m-3) & > 0 \\ 4m^2 - 32m + 48 & > 0 \, \, \text{(bagi 4)} \\ m^2 - 8m + 12 & > 0 \\ (m-2)(m-6) & > 0 \\ m = 2 \vee m & = 6 \end{align}$

HP3 = $ \{ m < 2 \vee m > 6 \} $
Sehingga HP = $ HP1 \cap HP2 \cap HP3 = \{ \frac{3}{2} < m < 2 \vee m > 6 \} $
Jadi, solusinya $ HP = \{ \frac{3}{2} < m < 2 \vee m > 6 \} . \heartsuit $
$ \rightarrow a=4, b= -2m, c = 2m-3 $
$\spadesuit \, $ Syarat akar real beda positif
$ x_1+x_2 > 0, \, x_1.x_2 > 0 , \, D > 0 $
$\spadesuit \, $ Menyelesaikan syarat-syaratnya
*) $ x_1+x_2 > 0 \rightarrow \frac{-b}{a} > 0 \rightarrow \frac{-(-2m)}{4} > 0 \rightarrow m > 0 \, $ ....(HP1)
*) $ x_1.x_2 > 0 \rightarrow \frac{c}{a} > 0 \rightarrow \frac{2m-3}{4} > 0 \rightarrow m > \frac{3}{2} \, $ ....(HP2)
*) syarat $ D > 0 $
$\begin{align} D & > 0 \\ b^2-4ac & > 0 \\ (-2m)^2-4.4.(2m-3) & > 0 \\ 4m^2 - 32m + 48 & > 0 \, \, \text{(bagi 4)} \\ m^2 - 8m + 12 & > 0 \\ (m-2)(m-6) & > 0 \\ m = 2 \vee m & = 6 \end{align}$

HP3 = $ \{ m < 2 \vee m > 6 \} $
Sehingga HP = $ HP1 \cap HP2 \cap HP3 = \{ \frac{3}{2} < m < 2 \vee m > 6 \} $
Jadi, solusinya $ HP = \{ \frac{3}{2} < m < 2 \vee m > 6 \} . \heartsuit $
Nomor 7
Himpunan penyelesaian pertaksamaan :
$ 2 \log (x-2) \leq \log (2x-1) \, $ adalah .....
$\clubsuit \, $ Konsep dasar
${}^a \log b = c , \, $ syaratnya : $ a > 0, a\neq 1, \, b > 0 $
$ {}^a \log b^n = n. {}^a \log b $
$ {}^a \log f(x) \leq {}^a \log g(x) \rightarrow f(x) \leq g(x) , \, $ syaratnya $ a > 1 $
$\clubsuit \, $ Menyelesaikan syarat logaritma
$ 2 \log (x-2) \leq \log (2x-1) \, $
Syarat :
$x-2 > 0 \rightarrow x > 2 $
$2x-1 > 0 \rightarrow x > \frac{1}{2} $
yang memenuhi kedua syarat adalah : HP1 = $ \{ x > 2 \} $
$\clubsuit \, $ Menyelesaikan pertidaksamaan
$\begin{align} 2 \log (x-2) & \leq \log (2x-1) \\ \log (x-2)^2 & \leq \log (2x-1) \, \, \text{(coret log nya)} \\ (x-2)^2 & \leq (2x-1) \\ (x-2)^2 & \leq (2x-1) \\ x^2 -4x + 4 & \leq (2x-1) \\ x^2 -4x + 4 - 2x + 1 & \leq 0 \\ x^2 -6x + 5 & \leq 0 \\ (x-1)(x-5) & \leq 0 \\ x=1 \vee x & = 5 \end{align}$

HP2 = $ \{ 1 \leq m \leq 5 \} $
Sehingga $ HP = HP1 \cap HP2 = \{ 2 < m \leq 5 \} $
Jadi, solusinya $ HP = \{ 2 < m \leq 5 \} . \heartsuit$
${}^a \log b = c , \, $ syaratnya : $ a > 0, a\neq 1, \, b > 0 $
$ {}^a \log b^n = n. {}^a \log b $
$ {}^a \log f(x) \leq {}^a \log g(x) \rightarrow f(x) \leq g(x) , \, $ syaratnya $ a > 1 $
$\clubsuit \, $ Menyelesaikan syarat logaritma
$ 2 \log (x-2) \leq \log (2x-1) \, $
Syarat :
$x-2 > 0 \rightarrow x > 2 $
$2x-1 > 0 \rightarrow x > \frac{1}{2} $
yang memenuhi kedua syarat adalah : HP1 = $ \{ x > 2 \} $
$\clubsuit \, $ Menyelesaikan pertidaksamaan
$\begin{align} 2 \log (x-2) & \leq \log (2x-1) \\ \log (x-2)^2 & \leq \log (2x-1) \, \, \text{(coret log nya)} \\ (x-2)^2 & \leq (2x-1) \\ (x-2)^2 & \leq (2x-1) \\ x^2 -4x + 4 & \leq (2x-1) \\ x^2 -4x + 4 - 2x + 1 & \leq 0 \\ x^2 -6x + 5 & \leq 0 \\ (x-1)(x-5) & \leq 0 \\ x=1 \vee x & = 5 \end{align}$

HP2 = $ \{ 1 \leq m \leq 5 \} $
Sehingga $ HP = HP1 \cap HP2 = \{ 2 < m \leq 5 \} $
Jadi, solusinya $ HP = \{ 2 < m \leq 5 \} . \heartsuit$
Nomor 8
$\displaystyle \lim_{x \to 0} \frac{7x^2 + \sin (2x^2) }{\tan ^2 3x} = ...... $
$\spadesuit \, $ Konsep limit
$ \displaystyle \lim_{x \to 0 } \frac{ax}{\tan bx} = \frac{a}{b} \, $ dan $ \, \, \displaystyle \lim_{x \to 0 } \frac{\sin ax}{\tan bx} = \frac{a}{b} $
$\spadesuit \, $ Menyelesaikan limitnya
$\begin{align} \displaystyle \lim_{x \to 0} \frac{7x^2 + \sin (2x^2) }{\tan ^2 3x} & = \displaystyle \lim_{x \to 0} \frac{7x^2 }{\tan ^2 3x} + \frac{ \sin (2x^2) }{\tan ^2 3x} \\ & = \frac{7}{3^2} + \frac{2}{3^2} \\ & = \frac{7}{9} + \frac{2}{9} = \frac{9}{9} = 1 \end{align}$
Jadi, nilai limitnya adalah 1. $ \heartsuit$
$ \displaystyle \lim_{x \to 0 } \frac{ax}{\tan bx} = \frac{a}{b} \, $ dan $ \, \, \displaystyle \lim_{x \to 0 } \frac{\sin ax}{\tan bx} = \frac{a}{b} $
$\spadesuit \, $ Menyelesaikan limitnya
$\begin{align} \displaystyle \lim_{x \to 0} \frac{7x^2 + \sin (2x^2) }{\tan ^2 3x} & = \displaystyle \lim_{x \to 0} \frac{7x^2 }{\tan ^2 3x} + \frac{ \sin (2x^2) }{\tan ^2 3x} \\ & = \frac{7}{3^2} + \frac{2}{3^2} \\ & = \frac{7}{9} + \frac{2}{9} = \frac{9}{9} = 1 \end{align}$
Jadi, nilai limitnya adalah 1. $ \heartsuit$
Nomor 9
Himpunan penyelesaian pertaksamaan $ x^2 - |x| \leq 6 \, $ adalah .....
$\clubsuit \, $ Konsep Harga mutlak
$ |x| = \left\{ \begin{array}{cc} x & , \text{ untuk } \, x \geq 0 \\ & \text{(atau)} \\ -x & , \text{ untuk } \, x < 0 \\ \end{array} \right. $
$\clubsuit \, $ penyelesaian dibagi menjadi dua kasus
*) untuk $ x \geq 0 , \, $ maka $ \, |x| = x $
$\begin{align} x^2 - |x| & \leq 6 \, \, \text{ (ganti } \, |x| = x ) \\ x^2 - x & \leq 6 \\ x^2 - x - 6 & \leq 0 \\ (x+2)(x-3) & \leq 0 \\ x=-2 \vee x & = 3 \end{align}$
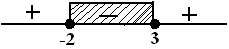
dari syarat $ x \geq 0 \, $, maka solusinya : HP1 = $ \{ 0 \leq x \leq 3 \} $
*) untuk $ x < 0 , \, $ maka $ \, |x| = -x $
$\begin{align} x^2 - |x| & \leq 6 \, \, \text{ (ganti } \, |x| = -x ) \\ x^2 - (-x) & \leq 6 \\ x^2 + x - 6 & \leq 0 \\ (x-2)(x+3) & \leq 0 \\ x=2 \vee x & = -3 \end{align}$

dari syarat $ x < 0 \, $, maka solusinya : HP2 = $ \{ -3 \leq x < 0 \} $
sehingga solusinya : HP = $ HP1 \cup HP2 = \{ -3 \leq x \leq 3 \} $
Jadi, solusinya $ HP = \{ -3 \leq x \leq 3 \} . \heartsuit $
$ |x| = \left\{ \begin{array}{cc} x & , \text{ untuk } \, x \geq 0 \\ & \text{(atau)} \\ -x & , \text{ untuk } \, x < 0 \\ \end{array} \right. $
$\clubsuit \, $ penyelesaian dibagi menjadi dua kasus
*) untuk $ x \geq 0 , \, $ maka $ \, |x| = x $
$\begin{align} x^2 - |x| & \leq 6 \, \, \text{ (ganti } \, |x| = x ) \\ x^2 - x & \leq 6 \\ x^2 - x - 6 & \leq 0 \\ (x+2)(x-3) & \leq 0 \\ x=-2 \vee x & = 3 \end{align}$

dari syarat $ x \geq 0 \, $, maka solusinya : HP1 = $ \{ 0 \leq x \leq 3 \} $
*) untuk $ x < 0 , \, $ maka $ \, |x| = -x $
$\begin{align} x^2 - |x| & \leq 6 \, \, \text{ (ganti } \, |x| = -x ) \\ x^2 - (-x) & \leq 6 \\ x^2 + x - 6 & \leq 0 \\ (x-2)(x+3) & \leq 0 \\ x=2 \vee x & = -3 \end{align}$

dari syarat $ x < 0 \, $, maka solusinya : HP2 = $ \{ -3 \leq x < 0 \} $
sehingga solusinya : HP = $ HP1 \cup HP2 = \{ -3 \leq x \leq 3 \} $
Jadi, solusinya $ HP = \{ -3 \leq x \leq 3 \} . \heartsuit $
Nomor 10
Titik P(a,b) dicerminkan terhadap sumbu X, bayangannya dicerminkan pula terhadap sumbu Y, maka bayangan terakhir titik P
merupakan ......
A. Pencerminan titik P terhadap garis $ y = x $
B. Pencerminan titik P terhadap garis $ y = -x $
C. Pencerminan titik P terhadap garis sumbu Y
D. Perputaran titik P dengan pusat titik O(0,0) sebesar $ \pi $ radian berlawanan perputaran jarum jam
E. Perputaran titik P dengan pusat titik O(0,0) sebesar $ \frac{\pi}{2} $ radian berlawanan perputaran jarum jam
A. Pencerminan titik P terhadap garis $ y = x $
B. Pencerminan titik P terhadap garis $ y = -x $
C. Pencerminan titik P terhadap garis sumbu Y
D. Perputaran titik P dengan pusat titik O(0,0) sebesar $ \pi $ radian berlawanan perputaran jarum jam
E. Perputaran titik P dengan pusat titik O(0,0) sebesar $ \frac{\pi}{2} $ radian berlawanan perputaran jarum jam
$\spadesuit \, $ Menentukan matriks gabungan
$ T_1 = $ (pencerminan sumbu X) $ = \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
$ T_2 = $ (pencerminan sumbu Y) $ = \left( \begin{matrix} -1 & 0 \\ 0 & 1 \end{matrix} \right) $
Matriks gabungannya (MT) :
$ MT = T_2.T_1 = \left( \begin{matrix} -1 & 0 \\ 0 & 1 \end{matrix} \right)\left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) $
$\spadesuit \, $ Matriks transformasi $ \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \, $ sama dengan matriks perputaran sebesar $ \pi \, $ berlawanan jarum jam
$\begin{align} MT & = \left( \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{matrix} \right) \\ & = \left( \begin{matrix} \cos \pi & -\sin \pi \\ \sin \pi & \cos \pi \end{matrix} \right) \\ & = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \end{align}$
Jadi, solusinya opsi D. $ \heartsuit $
$ T_1 = $ (pencerminan sumbu X) $ = \left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) $
$ T_2 = $ (pencerminan sumbu Y) $ = \left( \begin{matrix} -1 & 0 \\ 0 & 1 \end{matrix} \right) $
Matriks gabungannya (MT) :
$ MT = T_2.T_1 = \left( \begin{matrix} -1 & 0 \\ 0 & 1 \end{matrix} \right)\left( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right) = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) $
$\spadesuit \, $ Matriks transformasi $ \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \, $ sama dengan matriks perputaran sebesar $ \pi \, $ berlawanan jarum jam
$\begin{align} MT & = \left( \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{matrix} \right) \\ & = \left( \begin{matrix} \cos \pi & -\sin \pi \\ \sin \pi & \cos \pi \end{matrix} \right) \\ & = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \end{align}$
Jadi, solusinya opsi D. $ \heartsuit $



