Pembahasan Soal SPMK UB Matematika IPA Kode 81 tahun 2008 nomor 11 sampai 15


Nomor 11
Petunjuk C digunakan untuk menjawab soal nomor 11 dan 15.
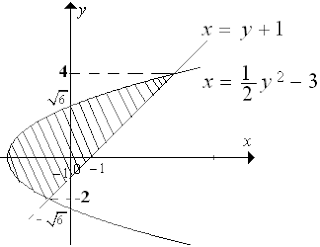
Jika $ \alpha \, $ memenuhi persamaan $ \sin x = \sqrt{2\cos x } \, $ maka
(1). $ \cos \alpha = -1 + \sqrt{2} $
(2). $ \sin \alpha = \sqrt{2 + 2\sqrt{2}} $
(3). $ \tan \alpha = \frac{\sqrt{2\sqrt{2}-2}}{-1+\sqrt{2}} $
(4). $ \cos \alpha = 1 - \sqrt{2} $
$\clubsuit \,$ Konsep dasar
*). identitas trigonometri
$ \sin ^2 x + \cos ^2 x = 1 \rightarrow \sin ^2 x = 1 - \cos ^2 x $
*). dari bentuk $ \sin x = \sqrt{2\cos x } \, $ , maka nilai $ \sin x \, $ dan $ \cos x \, $ positif.
$\clubsuit \,$ Menentukan nilai $ \cos x $
$\begin{align} \sin x & = \sqrt{2\cos x } \, \, \, \, \text{(kuadratkan)} \\ \sin ^2 x & = 2 \cos x \, \, \, \, \text{(gunakan identitas)} \\ 1 - \cos ^2 x & = 2 \cos x \\ \cos ^2 x + 2 \cos x - 1 & = 0 \\ \text{Misalkan } \, p & = \cos x > 0 \\ p^2 + 2 p - 1 & = 0 \, \, \, \, \text{(gunakan rumus ABC)} \\ a = 1, \, b = 2 , \, & \, c = -1 \\ p & = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \\ p & = \frac{-2 \pm \sqrt{2^2-4.1.(-1)}}{2.1} \\ p & = \frac{-2 \pm \sqrt{8}}{2} \\ p & = \frac{-2 \pm 2\sqrt{2}}{2} \\ p & = -1 \pm \sqrt{2} \end{align}$
Karena nilai $ \cos x \, $ positif, maka yang memenuhi adalah $ \cos \alpha = \cos x = -1 + \sqrt{2} $
$\clubsuit \,$ Buat segitiga dari $ \cos \alpha = \frac{-1 + \sqrt{2}}{1} = \frac{sa}{mi} $
spmk_ub_3_2008
Dari segitiga di atas diperoleh :
$\begin{align} \sin \alpha & = \frac{de}{mi} = \frac{\sqrt{2\sqrt{2}-2}}{1} = \sqrt{2\sqrt{2}-2} \\ \tan \alpha & = \frac{de}{sa} = \frac{\sqrt{2\sqrt{2}-2}}{-1 + \sqrt{2}} \end{align}$
Sehingga yang benar adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, jawabannya B. $ \heartsuit $
Nomor 12
Petunjuk C digunakan untuk menjawab soal nomor 11 dan 15.
Jika gambar di bawah ini adalah grafik $ y = \frac{df(x)}{dx} \, $ , maka dapat disimpulkan bahawa $ f(x) $
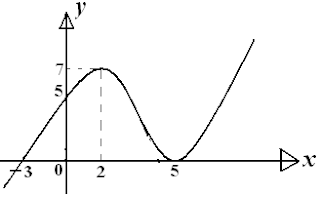
spmk_ub_1_2008
(1). mempunyai nilai minimum lokal pada $ x = -3 $
(2). turun pada interval $ x < -3 $
(3). mempunyai titik belok pada $ x = 5 $
(4). mempunyai nilai maksimum lokal pada $ x = 2 $
$\spadesuit \, $ Konsep dasar turunan
$ f^\prime (x) > 0 \rightarrow \, $ fungsi $ f(x) \, $ naik
$ f^\prime (x) < 0 \rightarrow \, $ fungsi $ f(x) \, $ turun
$\spadesuit \, $ Dari gambar pada soal, akar-akarnya (titik potong sumbu X) adalah -3 dan 5, artinya $ f^\prime (x) = 0 \, $ akar-akarnya -3 dan 5. Untuk memudahkan menganalisa fungsi aslinya $ f(x) \, $ , kita gambar dulu garis bilangan turunannya $ f^\prime (x) $ .
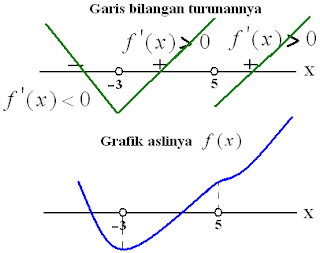
spmk_ub_4_2008
Keterangan grafik fungsi $ f(x) $ di atas :
*). mempunyai nilai minimum lokal pada $ x = -3 $
*). turun pada interval $ x < -3 $
*). mempunyai titik belok pada $ x = 5 $
sehingga pernyataan yang benar adalah (1), (2), dan (3).
Jadi, pernyataan yang benar adalah (1), (2), dan (3). $ \heartsuit $
Nomor 13
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Diketahui $ {}^2 \log a > 1 \, $ dan $ {}^2 \log b > 1, \, $ sedangkan $ a \neq b . \, $ Hubungan antara $ a \, $ dan $ b \, $ yang berlaku adalah .....
(1). $ \frac{a}{b} > 1 $
(2). $ \frac{b}{a} > 1 $
(3). $ a-b > 1 $
(4). $ a.b> 4 $
$\clubsuit \,$ Konsep pertidaksamaan logaritma
$ {}^c \log f(x) > {}^c \log g(x) \rightarrow f(x) > g(x) $
dengan syarat : $ c > 1 \, $ (basisnya > 1)
$\clubsuit \,$ Menentukan nilai $ a \, $ dan $ b $
$\begin{align} {}^2 \log a > 1 \rightarrow {}^2 \log a & > {}^2 \log 2 \\ a & > 2 \, \, \, \, \text{...(i)} \\ {}^2 \log b > 1 \rightarrow {}^2 \log b & > {}^2 \log 2 \\ b & > 2 \, \, \, \, \text{...(ii)} \end{align}$
Dari (i) dan (ii) diperoleh :
$ a.b > 2.2 \rightarrow a.b > 4 $
sehingga yang benar adalah pernyataan (4), berdasarkan petunjuk C jawabannya D.
Jadi, jawabannya D. $ \heartsuit $
Nomor 14
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Jika $ \overline{p} \vee \overline{q} \, $ adalah pernyataan benar, maka
(1). $ \overline{p} \wedge q \, $ benar
(2). $ \overline{q} \Rightarrow p \, $ benar
(3). $ \overline{p} \Leftrightarrow \overline{q} \, $ benar
(4). $ \overline{p} \wedge \overline{q} \, $ salah
$\spadesuit \, $ Tabel kebenaran logika matematika
spmk_ub_5_2008
Keterangan : B = Benar dan S = Salah
$\spadesuit \, $ Untuk menyelesaiakan soal ini, kita langsung menggunakan tabel kebenarannya
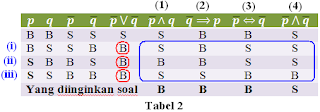
spmk_ub_6_2008
$ \overline{p} \vee \overline{q} \, $ adalah pernyataan benar, sehingga yang digunakan hanya baris yang nilai $ \overline{p} \vee \overline{q} \, $ juga benar (lihat kolom $ \overline{p} \vee \overline{q} \, $ yang kolomnya dilingkari merah) yaitu baris (i), (ii), dan (iii) yang diberi warna biru.
$\spadesuit \, $ Berdasarkan petunjuk C, yang diinginkan soal : BBBS
Kita cocokkan ketiga baris yang memenuhi, dan kalau ada yang sama maka diinggap benar. Cuma perhatikan 4 kolom yang diberi kotak biru saja, kemudian samakan dengan yang diinginkan soal yaitu : BBBS .
Baris (i) , Hasilnya SBSS , yang sama pernyataan (2) dan (4), bedasarkan petunjuk C jawabannya C
Baris (ii) , Hasilnya BBSS , yang sama pernyataan (1), (2) dan (4), bedasarkan petunjuk C tidak ada jawabannya
Baris (iii) , Hasilnya SSBB , yang sama pernyataan (3) saja, bedasarkan petunjuk C tidak ada jawabannya
Sehingga yang benar dan cocok dengan petunjuk C adalah barisan (i) yang jawabannya C.
Jadi, pernyataan yang sama adalah (2), dan (4), jawabannya C. $ \heartsuit $
Nomor 15
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Interval yang memenuhi pertidaksamaan $ x - 1 \leq \frac{2}{x} \, $ adalah ....
(1). $ x \leq -1 $
(2). $ -1 \leq x < 0 $
(3). $ 0 < x \leq 2 $
(4). $ -1 \leq x \leq 2 , \, \, x \neq 0 $
$\clubsuit \,$ Menyelesaikan pertidaksamaannya
$\begin{align} x - 1 & \leq \frac{2}{x} \\ (x - 1) - \frac{2}{x} & \leq 0 \\ \frac{x(x - 1)-2}{x} & \leq 0 \\ \frac{x^2 - x-2}{x} & \leq 0 \\ \frac{(x+1)(x-2)}{x} & \leq 0 \\ x = -1 , \, x= 2, \, x & = 0 \end{align}$
spmk_ub_7_2008
Solusinya : $ HP = \{ x \leq -1 \vee 0 < x \leq 2 \} $
Sehingga pernyataan yang benar sesuai dengan solusi di atas adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, yang benar pernyataan (1) dan (3), jawabannya B. $ \heartsuit $
Nomor Soal Lainnya : 1-5 6-10 11-15

Diposting oleh Tidak ada komentar:

Pembahasan Soal SPMK UB Matematika IPA Kode 81 tahun 2008 nomor 6 sampai 10


Nomor 6
Luas daerah yang dibatasi oleh garis $ y = x-1 \, $ dan parabola $ y^2 = 2x + 6 \, $ adalah .... satuan.
$\spadesuit \, $ gambar
$ y = x-1 \rightarrow x = y+1 $
$ y^2 = 2x + 6 \rightarrow x = \frac{1}{2}y^2 - 3 $
spmk_ub_2_2008
Titik potong kedua kurva :
$\begin{align} x_1 & = x_2 \\ \frac{1}{2}y^2 - 3 & = y + 1 \, \, \, \, \text{(kalii 2)} \\ y^2 -6 & = 2y + 2 \\ y^2 - 2y -8 & = 0 \\ (y-4)(y+2) & = 0 \\ y=4 \vee y & = -2 \end{align}$
$\spadesuit \, $ Menentukan luas daerah arsiran
$\begin{align} L & = \int \limits_{-2}^4 \text{ (kurva kanan)} - \text{ (kurva kiri)} dy \\ L & = \int \limits_{-2}^4 (y+1) - (\frac{1}{2}y^2 - 3) dy \\ L & = \int \limits_{-2}^4 ( -\frac{1}{2}y^2 + y + 4 ) \, dy \\ L & = ( -\frac{1}{6}y^3 + \frac{1}{2}y^2 + 4y )|_{-2}^4 \\ L & = ( -\frac{1}{6}.4^3 + \frac{1}{2}.4^2 + 4.4 ) - \\ & ( -\frac{1}{6}.(-2)^3 + \frac{1}{2}.(-2)^2 + 4.(-2) ) \\ L & = ( -\frac{32}{3} + 8 + 16 ) - ( \frac{4}{3} + 2 + -8 ) \\ L & = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $

Cara II :
$\spadesuit \, $ Luas daerah tertutup yang dibatasi oleh dua kurva (garis dengan parabola atau parabola dengan parabola) adalah $ L = \frac{D\sqrt{D}}{6a^2} \, $ dengan $ D = b^2-4ac $
$\spadesuit \, $ Substitusi garis ke parabola
$\begin{align} y & = x - 1 \rightarrow x = y+1 \\ y^2 & = 2x + 6 \rightarrow x = \frac{1}{2} y^2 - 3 \\ \frac{1}{2} y^2 - 3 & = y+1 \\ \frac{1}{2} y^2 -y -4 & = 0 \rightarrow a = \frac{1}{2}, \, b = -1, \, c = -4 \\ D & = b^2 - 4ac \\ D & = (-1)^2 - 4.(\frac{1}{2}).(-4) = 1 + 8 = 9 \\ L & = \frac{D\sqrt{D}}{6a^2} = \frac{9\sqrt{9}}{6.(\frac{1}{2})^2} = 18 \end{align}$
Jadi, luas daerahnya adalah 18. $ \heartsuit $
Nomor 7
$ \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} = ..... $
Cara I : Menggunakan turunan
$\clubsuit \,$ Penerapan turunan pada limit
$ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \, $ solusinya $ \displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to k } \frac{f^\prime (x)}{g^\prime (x)} \, $ diturunkan sampai hasilnya tidak $ \frac{0}{0} $
Turunan akar : $ y = \sqrt{f(x)} \rightarrow y^\prime = \frac{f^\prime (x)}{2\sqrt{f(x)}} $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\frac{1}{2\sqrt{x}} - 1}{1-2x} \\ & = \frac{\frac{1}{2\sqrt{1}} - 1}{1-2.1} \\ & = \frac{\frac{1}{2} - 1}{1-2} = \frac{-\frac{1}{2}}{-1} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $

Cara II : Merasionalkan bentuk akar
$\clubsuit \,$ Konsep kali sekawan
$ (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) = (\sqrt{p})^2-(\sqrt{q})^2 = p-q $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} . \frac{\sqrt{x} + x}{\sqrt{x} + x} \\ & = \displaystyle \lim_{x \to 1 } \frac{(x-x^2)}{(x-x^2)(\sqrt{x} + x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{1}{(\sqrt{x} + x)} \\ & = \frac{1}{(\sqrt{1} + 1)} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $

Cara III : Pemfaktoran
$\clubsuit \,$ Konsep pemfaktoran : $ p-q = (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) $
$\clubsuit \,$ Menentukan hasil limitnya
$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-\sqrt{x})(1+\sqrt{x})} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}}{x(1+\sqrt{x})} \\ & = \frac{\sqrt{1}}{1.(1+\sqrt{1})} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah $ \frac{1}{2} . \heartsuit $
Nomor 8
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jika nilai terkecil dan terbesar dari fungsi $ f(x) = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \, $ adalah $ a \, $ dan $ b \, $ ,
maka nilai $ a + b = 6 $
                         SEBAB
$ a = -5 \, $ dan $ b = 11 . $
$\spadesuit \, $ Konsep dasar trigonometri
*) $ \cos A \cos B = \frac{1}{2} [\cos (A+B) + \cos (A-B) ] $
*) Nilai maksimum/minimum dari : $ f(x) = P\cos g(x) + c \, $
$ f_\text{maks} = |P| + c \, $ dan $ f_\text{min} = -|P| + c $
$\spadesuit \, $ Menyederhanakan soalnya
Misal : $ A = \left( x - \frac{\pi}{4} \right) \, $ dan $ B = \left( x + \frac{\pi}{4} \right) $
$ A + B = \left( x - \frac{\pi}{4} \right) + \left( x + \frac{\pi}{4} \right) = 2x $
$ A - B = \left( x - \frac{\pi}{4} \right) - \left( x + \frac{\pi}{4} \right) = \frac{-\pi}{2} $
Substitusi nilai $ A \, $ dan $ B \, $ pada fungsinya :
$\begin{align} f(x) & = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \\ f(x) & = 8 \cos A \cos B + 3 \\ f(x) & = 8 .\frac{1}{2} . [\cos (A+B) + \cos (A-B) ] + 3 \\ f(x) & = 4 [\cos (2x) + \cos (\frac{-\pi}{2}) ] + 3 \\ f(x) & = 4 [\cos (2x) + 0 ] + 3 \\ f(x) & = 4 \cos (2x) + 3 \end{align}$
$\spadesuit \, $ Menentukan nilai maksimum dan minimum fungsi
$\begin{align} f(x) & = 4 \cos (2x) + 3 \rightarrow P = 4 , \, c = 3 \\ a & = f_\text{maks} = |P| + c = |4| + 3 = 4+3 = 7 \\ b & = f_\text{min} = -|P| + c = -|4| + 3 = -4+3 = -1 \end{align}$
Sehingga nilai : $ a +b = 7 + (-1) = 6 $
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : $ a + b = 6 \, $ (benar)
Pernyataan kedua : $ a = -5 , \, b = 11 \, $ (salah , karena seharusnya $ a = 7, \, b=-1$)
Karena pernyataan pertama benar dan pernyataan kedua salah, berdasarkan petunjuk B jawabannya adalah C.
Jadi, jawabannya C. $ \heartsuit $
Nomor 9
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jumlah $ n \, $ suku pertama suatu deret aritmetika dinyatakan dengan $ s_n = 2n^2 - n \, $ . Suku ke-12 deret tersebut adalah 45.
                         SEBAB
Deret tersebut mempunyai suku pertama $ a = 1 \, $ dan beda $ b = 4 . $
$\clubsuit \,$ Konsep Dasar Barisan aritmetika
$ u_n = a+(n-1)b, \, \, u_n = s_n - s_{n-1} , \, $ dan $ b = u_n - u_{n-1} $
$\clubsuit \,$ Menentukan nilai $ a \, $ dan $ b $
$\begin{align} s_n & = 2n^2 - n \\ a & = u_1 = s_1 = 2.1^2 - 1 = 1 \\ u_2 & = s_2 - s_1 \\ u_2 & = (2.2^2 - 2) - 1 = 6 - 1 = 5 \\ b & = u_2 - u_1 = 5 - 1 = 4 \end{align}$
sehingga nilai $ a = 1 \, $ dan $ b = 4 $
$\clubsuit \,$ Menentukan suku ke-12
$\begin{align} u_n & = a+(n-1)b \\ u_{12} & = 1+(12-1).4 \\ u_{12} & = 1+44 \\ u_{12} & = 45 \end{align}$
sehingga nilai $ u_{12} = 45 $
$\clubsuit \,$ Berdasarkan petunjuk B
Pernyataan pertama : $ u_{12} = 45 \, $ (benar)
Pernyataan kedua : $ a = 1 \, $ dan $ b = 4 \, $ (benar)
Karena kedua pernyataan benar dan saling berhubungan, maka berdasarkan petunjuk B jawabannya A.
Jadi, jawabannya A. $ \heartsuit $
Nomor 10
Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Apabila $ a = 0 \, $ dan $ b \, $ sembarang, maka matriks $ \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \, $ tidak mempunyai invers .
                            SEBAB
Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol.
$\spadesuit \, $ Konsep Matriks
*) Determinan
$ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow Det(A) = ad-bc $
*) Suatu matriks tidak mempunyai invers jika nilai determinannya sama dengan nol.
$\spadesuit \, $ Menentukan determinan matriksnya
$\begin{align} A & = \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \\ Det(A) & = a.a - (a-b)(a+b) \\ Det(A) & = a^2 - (a^2-b^2) \\ Det(A) & = b^2 \end{align}$
Karena nilai $ b \, $ sembarang, maka nilai $ Det(A) \, $ tidak selalu sama dengan nol, artinya Det(A) nilainya bisa nol atau tidak nol, sehingga matriks tersebut bisa mempunyai invers atau juga bisa tidak punya invers.
$\spadesuit \, $ Berdasarkan petunjuk B
Pernyataan pertama : Matriks tidak punya invers (salah)
Pernyataan kedua : Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol. (Benar)
Karena pernyataan pertama salah dan pernyataan kedua benar, berdasarkan petunjuk B jawabannya D.
Jadi, jawabannya D. $ \heartsuit $
Nomor Soal Lainnya : 1-5 6-10 11-15

Diposting oleh Tidak ada komentar:

Pembahasan Soal SPMK UB Matematika IPA Kode 81 tahun 2008


Nomor 1
Siswa kelas A mempunyai nilai rata-rata 65. 25 siswa kelas B mempunyai nilai rata-rata 70. Jika nilai dari 35 siswa kelas C digabung dengan siswa kelas A dan siswa kelas B maka nilai rata-rata dari 100 siswa adalah 68. Nilai rata-rata 35 siswa kelas C adalah ....
$\spadesuit \, $ Konsep rata-rata gabungan
$ \overline{X}_\text{gb} = \frac{n_A.\overline{X}_\text{A}+n_B.\overline{X}_\text{B}+n_C.\overline{X}_\text{C}}{n_A+n_B+n_C} $
Keterangan :
$ \overline{X}_\text{gb} \, $ = rata-rata gabungan semua kelompok
$ \overline{X}_\text{A} \, $ = rata-rata kelompok A (siswa kelas A)
$ n_A \, $ = banyak anggota kelompok A (banyak siswa kelas A)
yang lainnya sejenis dengan keterangan di atas.
$\spadesuit \, $ Pada soal diketahui :
$ n_B = 25, \, \overline{X}_\text{B} = 70, \, n_C = 35 , \, \overline{X}_\text{C} = p , $
$ \overline{X}_\text{A}=65, \, \overline{X}_\text{gb} = 68 $
$ n_A+n_B+n_C = 100 \rightarrow n_A+25+35=100 \rightarrow n_A=40 $
$\spadesuit \, $ Menentukan rata-rata kelas C ( $ \overline{X}_\text{C} $ )
$\begin{align} \overline{X}_\text{gb} & = \frac{n_A.\overline{X}_\text{A}+n_B.\overline{X}_\text{B}+n_C.\overline{X}_\text{C}}{n_A+n_B+n_C} \\ 68 & = \frac{40.65+25.70+35.p}{100} \\ 6800 & = 2600+1750+35p \\ 6800 & = 4350+35p \\ 35p & = 6800-4350 = 2450 \\ p & = \frac{2450}{35} = 70 \end{align}$
Jadi, rata-rata kelas C adalah 70. $ \heartsuit $
Nomor 2
Diketahui $ f(x) = 2x+1 \, $ dan $ (g \circ f)(x)=4x-5 \, $ , maka $ g(x-1) = .... $
$\clubsuit \,$ Menentukan fungsi $ g(x) $
$\begin{align} (g \circ f)(x) & =4x-5 \\ g ( f(x) ) & =4x-5 \\ g ( 2x+1 ) & =4x-5 \\ \text{misalkan : } & p = 2x+1 \rightarrow x = \frac{p-1}{2} \\ g ( 2x+1 ) & =4x-5 \\ g ( p) & =4\left( \frac{p-1}{2} \right) -5 \\ g ( p) & =2p-2-5 \\ g ( p) & =2p-7 \end{align}$
sehingga fungsinya : $ g(x) = 2x-7 $
$\clubsuit \,$ Menentukan fungsi $ g(x-1) $
$\begin{align} g(x) & = 2x-7 \\ g(x-1) & = 2(x-1)-7 \\ g(x-1) & = 2x-2-7 \\ g(x-1) & = 2x-9 \end{align}$
Jadi, diperoleh $ g(x-1) = 2x-9 . \heartsuit $

Cara II :
$\clubsuit \,$ Menentukan fungsi $ g(x-1) $
$\begin{align} (g \circ f)(x) & =4x-5 \\ g ( f(x) ) & =4x-5 \\ g ( 2x+1 ) & =4x-5 \\ \text{ substi. } x= \frac{1}{2}p-1 \rightarrow g ( 2x+1 ) & =4x-5 \\ g ( 2(\frac{1}{2}p-1)+1 ) & =4(\frac{1}{2}p-1)-5 \\ g ( p-2+1 ) & =2p-4-5 \\ g ( p-1 ) & =2p-9 \end{align}$
sehingga fungsinya : $ g(x-1) = 2x-9 $
Jadi, diperoleh $ g(x-1) = 2x-9 . \heartsuit $
Nomor 3
Nilai maksimum dari fungsi $ {}^4 \log (x+5) + {}^4 \log (3-x) \, $ adalah .....
$\spadesuit \, $ Konsep dasar
Logaritma : $ {}^a \log b + {}^a \log c = {}^a \log (bc) $
FK : $ g(x) = ax^2 + bx + c \rightarrow g_\text{maks} = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} $
$\spadesuit \, $ Menyederhanakan soal
$\begin{align} y & = {}^4 \log (x+5) + {}^4 \log (3-x) \\ y & = {}^4 \log [(x+5).(3-x) ] \\ y & = {}^4 \log (-x^2-2x+15) \end{align}$
$\spadesuit \, $ Agar nilai $ y = {}^4 \log (-x^2-2x+15) \, $ maksimum, maka nilai $ (-x^2-2x+15) \, $ juga harus maksimum. Misal $ g(x) = -x^2-2x+15 \rightarrow a = -1, \, b = -2, \, c = 15 $
$\begin{align} g_\text{maks} & = \frac{b^2-4ac}{-4a} \\ g_\text{maks} & = \frac{(-2)^2-4.(-1).15}{-4.(-1)} = \frac{4+60}{4}= \frac{64}{4} =16 \end{align}$
$\spadesuit \, $ Menentukan nilai maksimum soalnya
$\begin{align} y & = {}^4 \log (-x^2-2x+15) \\ y_\text{maks} & = {}^4 \log g_\text{maks} \\ y_\text{maks} & = {}^4 \log 16 \\ y_\text{maks} & = 2 \end{align}$
Jadi, nilai maksimumnya adalah 2. $ \heartsuit $
Nomor 4
Dengan kenaikan harga BBM 30% sedangkan semua yang lain dianggap harganya tetap, pengeluaran bensin adalah 13% dari pendapatan. Pengeluaran bensin sebelum kenaikan adalah ..... dari pendapatan
$\clubsuit \,$ Permisalan
$ p \, $ = pendapatan total.
$ a \, $ = persentase pengeluaran bensin awal dari pendapatan
$ y \, $ = besarnya pengeluaran bensin awal = $ a.p = ap $
$ y_b \, $ = besarnya pengeluaran bensin setelah adanya kenaikkan
$\clubsuit \,$ BBM naik 30%
$\begin{align} y_b & = y + 30\% y \\ y_b & = 100\% y + 30\% y \\ y_b & = 130\% y \\ y_b & = 130\% ap \, \, \, \, \text{....(i)} \end{align}$
$\clubsuit \,$ Pengeluaran bensin setelah adanya kenaikkan 13% dari pendapatan
$ y_b = 13\% p \, \, \, \, \text{....(ii)} $
$\clubsuit \,$ Menentukan nilai $ a \, $ dari bentuk (i) dan (ii)
$\begin{align} \text{pers(i)} & = \text{pers(ii)} \\ 130\% ap & = 13\% p \\ a & = \frac{13\% p}{130\% p} \\ a & = \frac{1}{10} \\ a & = \frac{1}{10} . 100\% = 10\% \end{align}$
diperoleh nilai $ a = 10 \% \, $ , artinya persentase pengeluaran bensin awal dari pendapatan adalah 10% .
Jadi, pengeluaran bensil awal 10% dari pendapatan . $ \heartsuit $
Nomor 5
Garis singgung kurva $ f(x)=x+2\sqrt{x} \, $ di titik (4,8) memotong sumbu X dan sumbu Y masing-masing di titik $ (a,0) \, $ dan $ (0,b) \, $ . Nilai $ a + b = ..... $
$\spadesuit \, $ Konsep persamaan garis singgung (PGS)
PGS di titik $(x_1,y_1) \, $ adalah $ y-y_1 = m(x-x_1) \, $ ,
dengan $ m =f^\prime (x_1) $
$\spadesuit \, $ Menentukan turunan dan gradien di titik $ (x_1,y_1) = (4,8) $
$\begin{align} f(x) & = x+2\sqrt{x} = x + 2 x^\frac{1}{2} \\ f^\prime (x) & = 1 + \frac{1}{2}. 2 . x^{-\frac{1}{2}} \\ f^\prime (x) & = 1 + \frac{1}{\sqrt{x}} \\ m & = f^\prime (x_1) = f^\prime (4) \\ m & = 1 + \frac{1}{\sqrt{4}} = 1 + \frac{1}{2} = \frac{3}{2} \end{align}$
$\spadesuit \, $ Menentukan PGS di $ (x_1,y_1) = (4,8) \, $ dan $ m = \frac{3}{2} $
$\begin{align} y-y_1 & = m(x-x_1) \\ y-8 & = \frac{3}{2}(x-4) \\ y-8 & = \frac{3}{2}x-6 \\ y & = \frac{3}{2}x +2 \end{align}$
diperoleh PGS nya : $ y = \frac{3}{2}x +2 $
$\spadesuit \, $ Menentukan titik potong (tipot) sumbu-sumbu
*) tipot sumbu X : substitusi $ y = 0 $
$ y = \frac{3}{2}x +2 \rightarrow 0 = \frac{3}{2}x +2 \rightarrow x = -\frac{4}{3} $
sehingga titik $ (a,0) = (-\frac{4}{3},0) \, $ , artinya $ a = -\frac{4}{3} $
*) tipot sumbu Y : substitusi $ x = 0 $
$ y = \frac{3}{2}x +2 \rightarrow y = \frac{3}{2}.0 +2 \rightarrow y = 2 $
sehingga titik $ (0,b) = (0,2) \, $ , artinya $ b = 2 $
Nilai $ a + b = -\frac{4}{3} + 2 = \frac{3}{2} $
Jadi, nilai $ a + b = \frac{3}{2} . \heartsuit $
Nomor Soal Lainnya : 1-5 6-10 11-15

Diposting oleh Tidak ada komentar:
Label:

Petunjuk Pengerjaan soal SPMK UB


PETUNJUK UMUM

1. Sebelum mengerjakan soal, telitilah terlebih dahulu jumlah dan nomor halaman yang terdapat pada naskah ujian. Naskah ujian ini terdiri dari 11 halaman.
2. Tulis nama, tanggallahir, dan nomorpeserta Anda, serta kodesoal, dan tanggalujian pada lembar jawaban di tempat yang disediakan, sesuai petunjuk yang diberikan oleh petugas.
3. Bacalah dengan cermat setiap petunjuk yang menjelaskan cara menjawab soal.
4. Tulislah jawaban Anda pada lembar jawaban ujian (LJU) yang disediakan sesuai dengan cara dan petunjuk yang telah diberikan oleh petugas.
5. Untuk keperluan coret-mencoret , Anda dapat menggunakan tempat yang kososng pada naskah ujian ini. Jangan sekali-kali menggunakan LJU untuk keperluan itu.
6. Selama ujian, Anda tidak diperkenankan bertanya atau meminta penjelasan mengenai soal-soal ujian kepada siapapun, termasuk pengawas ujian.
7. Jawaban betul mendapat Skor 4, jawaban salah mendapat Skor -1, dan tidak dijawab mendapat Skor 0.
8. Setelah ujian selesai, Anda diharap tetap duduk tenang, sampai pengawas datang ke tempat Anda untuk mengumpulkan LJU.
9. Jagalah LJU agar tidakkotor, basah, teripat, atau sobek.
10. Kode naskah ujian ini adalah:


PETUNJUK KHUSUS

PETUNJUK A
Pilih satu jawaban yang paling tepat.

PETUNJUK B
Soal terdiri atas tiga bagian, yaitu: PERNYATAAN PERTAMA, kata “SEBAB”, dan PERNYATAAN KEDUA yang disusun berurutan.
Pilihlah:
A. jika pernyataan pertama benar, pernyataan kedua benar, ada hubungan sebab-akibat
B. jika pernyataan pertama benar, pernyataan kedua benar, tidak ada hubungan sebab-akibat
C. jika pernyataan pertama benar, pernyataan kedua salah
D. jika pernyataan pertama salah, pernyataan kedua benar
E. jika pernyataan pertama salah, pernyataan kedua salah

PETUNJUK C
Pilihlah:
A. jika 1, 2 , dan 3 yang benar
B. jika 1 dan 3 yang benar
C. jika 2 dan 4 yang benar
D. jika hanya 4 yang benar
E. jika semua jawaban benar

Untuk Petunjuk B, biasanya jarang dipakai oleh soal-soal seleksi masuk PTN khusus soal matematika. Akan tetapi SPMK UB pada tahun 2008 dan tahun 2009  (klik untuk melihat soalnya : nomor 10 dan nomor 11) pernah menggunakan Petunjuk B ini. Coba lihat juga contoh soal yang menggunakan petunjuk C : soal SPMK UB tahun 2013 nomor 14 dan 15.

Demikian untuk penulisan tentang Petunjuk Pengerjaan Soal SPMK UB , Semoga bermanfaat. Terima kasih.



Diposting oleh Tidak ada komentar:
Label:

Materi Matematika SMA kelas XI Peminatan Kurikulum 2013 (K-13)


Hallow Sobat, bagaimana keadaannya??? Mudah-mudahan baik-baik saja!!!!

            Berikut kami share Materi Matematika SMA kelas XI  Peminatan Kurikulum 2013 (K-13) yang harus dipelajari di tingkat kelas XI. Seperti biasa namanya materi peminatan  pasti materinya lebih mendalam dan akan sulit terutama untuk soal-soal latihannya. Tapi sya yakin, dengan ketekunan dan kesabaran serta lebih ulet lagi, pasti sobat akan bisa untuk materi pemintan ini. Silahkan baca materi wajibnya dengan klik Materi Matematika SMA kelasXI  Wajib Kurikulum 2013 (K-13)  . Berikut materi dan penjabarannya yang terdiri dari 9 materi atau bab  :


No.
Materi atau babnya
Deskripsi Materi
1.
polinomial
Mendeskripsikan konsep dan menganalisis sifat operasi aljabar pada polinomial dan menerapkannya dalam menyelesaikan masalah matematika.
Mendeskripsikan aturan perkalian dan pembagian polinomial dan menerapkan teorema sisa dan dan pemfaktoran polinomial dalam menyelesaikan masalah matematika
Memecahan masalah nyata menggunakan konsep teorema sisa dan faktorisasi dalam polinomial.
Memecahkan masalah nyata dengan model persamaan kubik dengan menerapkan aturan dan sifat pada polinomial.
2.
Irisan Kerucut
Menganalisis konsep sifat- sifat irisan kerucut (parabola, hiperbola, dan ellips) dan menerapkannya dalam pembuktian dan menyelesaikan masalah matematika
Mendeskripsikan hubungan garis direktis, titik fokus dan titik-titik pada kurva parabola, hiperbola, dan ellips dan menerapkannya dalam pemecahan masalah.
Menganalisis data terkait unsur-unsur parabola, hiperbola dan ellips untuk menggambar kurva dan mengidentifikasi sifat-sifatnya
Mengolah data dan menganalisis model matematika dengan melakukan manipulasi aljabar untuk menyelesaikan masalah nyata yang berkaitan dengan persamaan parabola atau hiperbola atau ellips.
Menyajikan objek-objek nyata sebagai gambaran model parabola, hiperbola, dan ellips dan merancang masalah serta menyelesaikannya dengan menerapkan konsep dan sifat-sifat irisan kerucut yang telah dibuktikan kebenaranya.
3
Irisan Dua Lingkaran
Mendeskripsikan konsep lingkaran dan menganalisis sifat-sifat irisan dua lingkaran dan menerapkannya dalam memecahkan masalah.
Merencanakan dan melaksanakan strategi yang efektif dalam memecahkan masalah nyata dengan model lingkaran yang saling beririsan, menginterpretasi masalah dalam gambar dan menyelesaikannya.
4.
Sampel  dan  Fungsi distribusi
Menganalisis penarikan sampel acak dari suatu populasi sekumpulan objek atau kejadian sehari-hari.
Mendeskripsikan konsep variabel acak, dan menganalisis untuk merumuskan fungsi distribusi binomial melalui percobaan acak.
Menyajikan dan menggunakan rumus fungsi distribusi binomial dalam menaksir suatu kejadian yang akan muncul berkaitan dengan percobaan acak
5.
Penarikan kesimpulan
Mengevaluasi penarikan kesimpulan melalui uji hipotesis dengan kriteria tertentu.
Menyajikan proses dan hasil penarikan kesimpulan dari uji hipotesis dengan argumentasi dan prosedur penarikan kesimpulan yang valid.
6.
Limit  Fungsi
Mendeskripsikan dan menganalisis konsep dan sifat-sifat limit fungsi trigonometri dan nilai limit fungsi aljabar menuju ketakhinggaan dan meng-gunakan  dalam pemecah-an berbagai masalah.
Menyajikan dan mengilustrasikan konsep limit dalam konteks nyata.
7.
Turunan  fungsi trigonometri
Mendeskripsikan konsep turunan fungsi trigonometri untuk menurunkan sifat-sifatnya serta menggunakannya dalam memecahkan masalah.
Merencanakan dan melaksanakan strategi yang efektif dan menyajikan model matematika dalam memecahkan masalah nyata tentang fungsi trigonometri.
8.
Turunan  fungsi trigonometri
(aplikasinya)
Menganalisis konsep dan sifat turunan fungsi trigonometri dan menerapkannya untuk menentukan titik stasioner (titik maximum, titik minimum dan titik belok).
Menyajikan, dan memecahkan masalah nyata yang berkaitan dengan turunan fungsi trigonometri.
9.
Aplikasi Turunan  Fungsi
Menganalisis bentuk model matematika berupa persamaan fungsi, serta menerapkan konsep dan sifat turunan fungsi dan garis singgung kurva dalam menaksir nilai fungsi dan nilai akar-akar persamaan aljabar
Menyajikan data dari situasi nyata, memilih variabel dan mengomunikasikannya dalam bentuk model matematika berupa persamaan fungsi, serta menerapkan konsep dan sifat turunan fungsi dan garis singgung kurva dalam menaksir nilai fungsi dan nilai akar-akar persamaan aljabar


Berikut link untuk materi kurikulum 2013 kelas X SMA :
MateriMatematika SMA kelas X Wajib Kurikulum 2013 (K-13)
MateriMatematika SMA kelas X Peminatan Kurikulum 2013 (K-13)

Jika total materi kelas XI SMA dari wajib dan peminatan, maka ada 12 + 9 = 21 materi atau bab yang harus dikuasai untuk kelas XI SMA, saya kira ini bukan jumlah yang sedikit. Tetap semangat sobat belajarnya.

Semoga bermanfaat. Terima kasih.

Diposting oleh Tidak ada komentar:
Label:
Langganan: Postingan (Atom)