Nomor 11
Enam orang tamu undangan akan dijemput dengan mobil yang masing-masing berkapasitas 4 orang. Banyak cara penempatan orang pada mobil adalah ...
$\spadesuit \, $ Dibagi menjadi beberapa kasus :
Kasus 1 : 4 orang MI dan 2 orang M2, cara = $C_4^6.C_2^2 = 15$
Kasus 2 : 3 orang MI dan 3 orang M2, cara = $C_3^6.C_3^3 = 20$
Kasus 3 : 2 orang MI dan 4 orang M2, cara = $C_2^6.C_4^4 = 15$
Total cara = 15 + 20 + 15 = 50 cara. Akan tetapi jawaban tidak ada.
Pejelasan :
Kasus 1 : $C_4^6.C_2^2 \, $ artinya memilih 4 orang dari 6 orang untuk ditempatkan pada mobil I ($C_4^6$) dan memilih 2 dari sisa yaitu 2 orang untuk ditempatkan pada mobil II ($C_2^2$). Sejenis penjelasannya dengan kasus yang lainnya. Sedangkan kombinasi digunakan karena urutan penempatan orang pada setiap mobil tidak berpengaruh (tidak memperhatikan urutan).
$\spadesuit \, $ Kemungkinan kasus yang diminta soal (soal kurang lengkap) adalah salah satu mobil harus penuh. Di soal ini juga tidak disebutkan ada berapa mobil yang digunakan. Berdasarkan kasus ini, ada dua kemungkinan yaitu :
Kasus 1 : 4 orang MI dan 2 orang M2, cara = $C_4^6.C_2^2 = 15$
Kasus 2 : 2 orang MI dan 4 orang M2, cara = $C_2^6.C_4^4 = 15$
Total cara = 15 + 15 = 30 cara
Jadi, cara penempatan orang pada mobil adalah 30 cara. $ \heartsuit $
Kasus 1 : 4 orang MI dan 2 orang M2, cara = $C_4^6.C_2^2 = 15$
Kasus 2 : 3 orang MI dan 3 orang M2, cara = $C_3^6.C_3^3 = 20$
Kasus 3 : 2 orang MI dan 4 orang M2, cara = $C_2^6.C_4^4 = 15$
Total cara = 15 + 20 + 15 = 50 cara. Akan tetapi jawaban tidak ada.
Pejelasan :
Kasus 1 : $C_4^6.C_2^2 \, $ artinya memilih 4 orang dari 6 orang untuk ditempatkan pada mobil I ($C_4^6$) dan memilih 2 dari sisa yaitu 2 orang untuk ditempatkan pada mobil II ($C_2^2$). Sejenis penjelasannya dengan kasus yang lainnya. Sedangkan kombinasi digunakan karena urutan penempatan orang pada setiap mobil tidak berpengaruh (tidak memperhatikan urutan).
$\spadesuit \, $ Kemungkinan kasus yang diminta soal (soal kurang lengkap) adalah salah satu mobil harus penuh. Di soal ini juga tidak disebutkan ada berapa mobil yang digunakan. Berdasarkan kasus ini, ada dua kemungkinan yaitu :
Kasus 1 : 4 orang MI dan 2 orang M2, cara = $C_4^6.C_2^2 = 15$
Kasus 2 : 2 orang MI dan 4 orang M2, cara = $C_2^6.C_4^4 = 15$
Total cara = 15 + 15 = 30 cara
Jadi, cara penempatan orang pada mobil adalah 30 cara. $ \heartsuit $
Nomor 12
Pada suatu malam yang gelap, seorang berdiri sejauh 5 meter dari sebuah lampu jalan yang tingginya 6 meter. Jika panjang bayangan orang tersebut
di daerah datar adalah $\frac{5}{3} $ meter, maka tinggi orang tersebut adalah ...
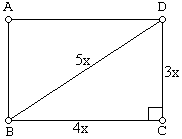
$\clubsuit \, $ Gambar :

$\clubsuit \, $ Konsep kesebangunan pada segitiga :
$\Delta$ADE sebangun dengan $\Delta$ABC
$\frac{DE}{BC}=\frac{AD}{AB} \rightarrow \frac{x}{6} = \frac{\frac{5}{3}}{\frac{20}{3}} \rightarrow x = \frac{3}{2} \, \text{m} = 150 \, \text{cm} $ .
Jadi, tinggi orang adalah 150 cm. $ \heartsuit $

$\clubsuit \, $ Konsep kesebangunan pada segitiga :
$\Delta$ADE sebangun dengan $\Delta$ABC
$\frac{DE}{BC}=\frac{AD}{AB} \rightarrow \frac{x}{6} = \frac{\frac{5}{3}}{\frac{20}{3}} \rightarrow x = \frac{3}{2} \, \text{m} = 150 \, \text{cm} $ .
Jadi, tinggi orang adalah 150 cm. $ \heartsuit $
Nomor 13
Banyaknya cara untuk menempatkan 3 anak laki-laki dan 2 anak prempuan duduk berjajar tanpa membedakan tiap anak adalah ...
$\spadesuit \, $ Karena tidak dibedakan, maka 3 anak laki-laki dianggap sama(identik/kembar), begitu juga 2 anak perempuan.
Sehingga kasus ini adalah termasuk permutasi berulang dengan menyusun ulang huruf LLLPP .
Total cara = $\frac{5!}{3!.2!} = 10 $ cara.
Jadi, banyaknya cara penempatan ada 10 cara. $ \heartsuit $
Total cara = $\frac{5!}{3!.2!} = 10 $ cara.
Jadi, banyaknya cara penempatan ada 10 cara. $ \heartsuit $
Nomor 14
Fungsi $f$ dan $g$ disebut saling simetris jika grafik $f$ dapat diperoleh dengan mencerminkan grafik $g$ terhadap sumbu X. Semua pasangan
fungsi berikut saling simetris, KECUALI ...
$\clubsuit \, f \, $ diperoleh dari mencerminkan $g$ terhadap sumbu X, ini artinya $f$ adalah bayangan dari $g$.
$\clubsuit \, $ Pencerminan terhadap sumbu X :
$(x,y) \leftrightarrow (x^\prime, y^\prime) = (x, -y) $
$y=g(x) \leftrightarrow y^\prime = -y = - g(x) \, $ atau $\, f(x) = -g(x)$
Artinya $f(x)$ diperoleh dari perkalian -1 dengan $g(x)$ .
$\clubsuit \, $ Opsi A yang tidak memenuhi karena $f(x)$ seharusnya
$f(x) = - g(x) = - (x^2+1) \rightarrow f(x) = -x^2 - 1$ .
Jadi, fungsi yang tidak simetris ada di opsi A . $\heartsuit $
$\clubsuit \, $ Pencerminan terhadap sumbu X :
$(x,y) \leftrightarrow (x^\prime, y^\prime) = (x, -y) $
$y=g(x) \leftrightarrow y^\prime = -y = - g(x) \, $ atau $\, f(x) = -g(x)$
Artinya $f(x)$ diperoleh dari perkalian -1 dengan $g(x)$ .
$\clubsuit \, $ Opsi A yang tidak memenuhi karena $f(x)$ seharusnya
$f(x) = - g(x) = - (x^2+1) \rightarrow f(x) = -x^2 - 1$ .
Jadi, fungsi yang tidak simetris ada di opsi A . $\heartsuit $
Nomor 15
Berdasarkan penelitian diketahui bahwa populasi hewan A berkurang menjadi setengahnya tiap 10 tahun. Pada tahun 2000 populasinya tinggal 1 juta.
Banyak populasi hewan A pada tahun 1960 sekitar ...
$\spadesuit \, $ Barisan geometri : $U_n = a.r^{n-1}$
$\spadesuit \, $ Menentukan nilai unsur-unsurnya :
* $a=U_1 \, $ menyatakan suku pertama pada tahun 1960.
* Setiap 10 tahun berkurang setengahnya, artinya rasio : $r = \frac{1}{2}$
* tahun 2000 dari tahun 1960 ada 5 suku (perubahan setiap 10 tahun) yaitu 1960, 1970, 1980, 1990, 2000.
* Tahun 2000 populasinya 1 juta, artinya $U_5 = 1$
$\spadesuit \, $ Menentukan nilai $a$ :
$\begin{align} U_5 & = ar^{5-1} \\ 1 & = a \times \left( \frac{1}{2} \right)^4 \\ 1 & = a \times \left( \frac{1}{16} \right) \\ a & = 16 \end{align}$
Jadi, populasi tahun 1960 sebesar 16 juta. $\heartsuit $
$\spadesuit \, $ Menentukan nilai unsur-unsurnya :
* $a=U_1 \, $ menyatakan suku pertama pada tahun 1960.
* Setiap 10 tahun berkurang setengahnya, artinya rasio : $r = \frac{1}{2}$
* tahun 2000 dari tahun 1960 ada 5 suku (perubahan setiap 10 tahun) yaitu 1960, 1970, 1980, 1990, 2000.
* Tahun 2000 populasinya 1 juta, artinya $U_5 = 1$
$\spadesuit \, $ Menentukan nilai $a$ :
$\begin{align} U_5 & = ar^{5-1} \\ 1 & = a \times \left( \frac{1}{2} \right)^4 \\ 1 & = a \times \left( \frac{1}{16} \right) \\ a & = 16 \end{align}$
Jadi, populasi tahun 1960 sebesar 16 juta. $\heartsuit $