Nomor 11
Diketahui $ P \, $ dan $ Q \, $ suatu polinomial sehingga $ P(x) = Q(x)(a^2x^3+(a-1)x+2a). \, $ Jika $ P(x) \, $ dan $ Q(x) \, $
masing-masing memberikan sisa 9 dan 1 apabila masing-masing dibagi $ x-1 , \, $ maka $ P(x)Q(x)(a^2x^3+(a-1)x+2a) \, $
dibagi $ x - 1 \, $ bersisa ....
$\clubsuit \, $ Teorema sisa : $\frac{f(x)}{x-a} \Rightarrow \text{sisa} = f(a)$
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
$ P(x) : (x-1), \, $ sisa = 9 , artinya $ P(1) = 9 \, $ ....pers(i)
$ Q(x) : (x-1), \, $ sisa = 1 , artinya $ Q(1) = 1 \, $ ....pers(ii)
$\clubsuit \, $ Substitusi $ x = 1 \, $ ke $ P(x) = Q(x)(a^2x^3+(a-1)x+2a) $
$\begin{align} x = 1 \rightarrow P(x) & = Q(x)(a^2x^3+(a-1)x+2a) \\ P(1) & = Q(1)(a^2.1^3+(a-1).1+2a) \\ 9 & = 1.(a^2+(a-1)+2a) \\ (a^2+(a-1)+2a) & = 9 \end{align}$
$\clubsuit \, $ Sisa pembagian $ P(x)Q(x)(a^2x^3+(a-1)x+2a) \, $ dengan $ x - 1 $
$ P(x)Q(x)(a^2x^3+(a-1)x+2a) : x - 1 $
sisanya = $ P(1)Q(1)(a^2.1^3+(a-1).1+2a) $
$\begin{align} \text{Sisa } \, & = P(1)Q(1)(a^2.1^3+(a-1).1+2a) \\ & = 9.1.(a^2+(a-1)+2a) \\ & = 9.1.9 \\ \text{Sisa } \, & = 81 \end{align}$
Jadi, sisa pembagiannya adalah 81. $ \heartsuit $
artinya : substitusi $x=a\, $ ke $f(x)$ dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
$ P(x) : (x-1), \, $ sisa = 9 , artinya $ P(1) = 9 \, $ ....pers(i)
$ Q(x) : (x-1), \, $ sisa = 1 , artinya $ Q(1) = 1 \, $ ....pers(ii)
$\clubsuit \, $ Substitusi $ x = 1 \, $ ke $ P(x) = Q(x)(a^2x^3+(a-1)x+2a) $
$\begin{align} x = 1 \rightarrow P(x) & = Q(x)(a^2x^3+(a-1)x+2a) \\ P(1) & = Q(1)(a^2.1^3+(a-1).1+2a) \\ 9 & = 1.(a^2+(a-1)+2a) \\ (a^2+(a-1)+2a) & = 9 \end{align}$
$\clubsuit \, $ Sisa pembagian $ P(x)Q(x)(a^2x^3+(a-1)x+2a) \, $ dengan $ x - 1 $
$ P(x)Q(x)(a^2x^3+(a-1)x+2a) : x - 1 $
sisanya = $ P(1)Q(1)(a^2.1^3+(a-1).1+2a) $
$\begin{align} \text{Sisa } \, & = P(1)Q(1)(a^2.1^3+(a-1).1+2a) \\ & = 9.1.(a^2+(a-1)+2a) \\ & = 9.1.9 \\ \text{Sisa } \, & = 81 \end{align}$
Jadi, sisa pembagiannya adalah 81. $ \heartsuit $
Nomor 12
Jika $3\sin x+4\cos y=5$, maka nilai minimum $3\cos x+4\sin y$ adalah ...
$\spadesuit \, $ Kuadratkan persamaan $3sinx+4cosy=5$:
$\begin{align} (3sinx+4cosy)^2&=5^2 \\ 9sin^2x+16cos^2y+24sinxcosy&=25 \, \, (sin^2z+cos^2z=1 )\\ 9(1-cos^2x)+16(1-sin^2y)+24sinxcosy&=25 \\ 9-9cos^2x+16-16sin^2y+24sinxcosy&=25 \\ 9cos^2x+16sin^2y&=24sinxcosy \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Misalkan $f=3cosx+4siny$, dikuadratkan:
$\begin{align} f^2&=(3cosx+4siny )^2 \\ f^2&=9cos^2x+16sin^2y+24cosxsiny \, \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers (i) ke pers(ii) :
$\begin{align} f^2&=9cos^2x+16sin^2y+24cosxsiny \\ &=24sinxcosy + 24cosxsiny \\ &=24(sinxcosy + cosxsiny) \\ f^2&=24sin(x+y) \end{align}$
$\spadesuit \, $ Nilai maksimum dari , $y=Asinf(x) \Rightarrow y_{max}=|A|$ :
$\begin{align} f^2&=24sin(x+y) \\ f^2&=|24| \\ f^2&=24 \\ f&=\pm \sqrt{24} = \pm 2\sqrt{6} \\ f_{min}&= - 2\sqrt{6} \end{align}$
Jadi, nilai minimum dari $3\cos x+4\sin y= - 2\sqrt{6}. \heartsuit $
$\begin{align} (3sinx+4cosy)^2&=5^2 \\ 9sin^2x+16cos^2y+24sinxcosy&=25 \, \, (sin^2z+cos^2z=1 )\\ 9(1-cos^2x)+16(1-sin^2y)+24sinxcosy&=25 \\ 9-9cos^2x+16-16sin^2y+24sinxcosy&=25 \\ 9cos^2x+16sin^2y&=24sinxcosy \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Misalkan $f=3cosx+4siny$, dikuadratkan:
$\begin{align} f^2&=(3cosx+4siny )^2 \\ f^2&=9cos^2x+16sin^2y+24cosxsiny \, \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers (i) ke pers(ii) :
$\begin{align} f^2&=9cos^2x+16sin^2y+24cosxsiny \\ &=24sinxcosy + 24cosxsiny \\ &=24(sinxcosy + cosxsiny) \\ f^2&=24sin(x+y) \end{align}$
$\spadesuit \, $ Nilai maksimum dari , $y=Asinf(x) \Rightarrow y_{max}=|A|$ :
$\begin{align} f^2&=24sin(x+y) \\ f^2&=|24| \\ f^2&=24 \\ f&=\pm \sqrt{24} = \pm 2\sqrt{6} \\ f_{min}&= - 2\sqrt{6} \end{align}$
Jadi, nilai minimum dari $3\cos x+4\sin y= - 2\sqrt{6}. \heartsuit $
Nomor 13
Diberitahukan kubus ABCD.EFGH dengan panjang rusuk $ 3p , \, $ titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD
sehingga BP = GQ = DR = $ p . \, $ Jika $ \beta \, $ adalah irisan bidang yang melalui P, Q, dan R, maka tangen sudut
antara bidang $ \beta \, $ dan bidang alas adalah ....
$\spadesuit \, $ Gambar

Bidang irisannya adalah bidang yang berwarna hijau. Sudut yang terbentuk antara bidang irisan dan bidang alas adalah sudut XYW. panjang $ XY = \frac{1}{2} AC = \frac{1}{2}3p\sqrt{2} = \frac{3p}{\sqrt{2}} $
$\spadesuit \, $ Menentukan nilai tangen sudut XYW
$\begin{align} \tan XYW & = \frac{XW}{XY} \\ & = \frac{3p}{\frac{3p}{\sqrt{2}}} = 3p . \frac{\sqrt{2}}{3p} \\ \tan XYW & = \sqrt{2} \end{align}$
Jadi, nilai tangennya adalah $ \sqrt{2} . \heartsuit $

Bidang irisannya adalah bidang yang berwarna hijau. Sudut yang terbentuk antara bidang irisan dan bidang alas adalah sudut XYW. panjang $ XY = \frac{1}{2} AC = \frac{1}{2}3p\sqrt{2} = \frac{3p}{\sqrt{2}} $
$\spadesuit \, $ Menentukan nilai tangen sudut XYW
$\begin{align} \tan XYW & = \frac{XW}{XY} \\ & = \frac{3p}{\frac{3p}{\sqrt{2}}} = 3p . \frac{\sqrt{2}}{3p} \\ \tan XYW & = \sqrt{2} \end{align}$
Jadi, nilai tangennya adalah $ \sqrt{2} . \heartsuit $
Nomor 14
Jika $A$ adalah matriks berukuran 2 x 2 dan
$\left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] = 5x^2-8x+1 $, maka matriks $A$
yang mungkin adalah ...
$\spadesuit \, $ Misalkan matriks $A=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \, $:
$\begin{align} \left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ \left[ \begin{matrix} x & 1 \end{matrix} \right] \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ \left[ \begin{matrix} ax+c & bx+d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ ax^2+(b+c)x+d&= 5x^2-8x+1 \end{align}$
$\spadesuit \, $ Diperoleh $a=5,d=1, \, $ dan $b+c=-8 $
Jadi, kemungkinan matriks $A$: $\, \, A=\left[ \begin{matrix} 5 & -3 \\ -5 & 1 \end{matrix} \right]\, \vee A=\left[ \begin{matrix} 5 & -8 \\ 0 & 1 \end{matrix} \right] \, \heartsuit $
Catatan : Mungkin ada kesalahan pada pengetikan pilihan (optionnya).
$\begin{align} \left[ \begin{matrix} x & 1 \end{matrix} \right] A \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ \left[ \begin{matrix} x & 1 \end{matrix} \right] \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ \left[ \begin{matrix} ax+c & bx+d \end{matrix} \right] \left[ \begin{matrix} x \\ 1 \end{matrix} \right] &= 5x^2-8x+1 \\ ax^2+(b+c)x+d&= 5x^2-8x+1 \end{align}$
$\spadesuit \, $ Diperoleh $a=5,d=1, \, $ dan $b+c=-8 $
Jadi, kemungkinan matriks $A$: $\, \, A=\left[ \begin{matrix} 5 & -3 \\ -5 & 1 \end{matrix} \right]\, \vee A=\left[ \begin{matrix} 5 & -8 \\ 0 & 1 \end{matrix} \right] \, \heartsuit $
Catatan : Mungkin ada kesalahan pada pengetikan pilihan (optionnya).
Nomor 15
Misalkan $A(t)$ menyatakan luas daerah di bawah kurva $y=bx^2 , 0\leq x \leq t$. Jika titik $P(x_0,0)$ sehingga $A(x_0):A(1)=1:8$, maka perbandingan
luas trapesium $ABPQ:DCPQ=...$


$\spadesuit \, $ Menentukan $A(t)$:
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
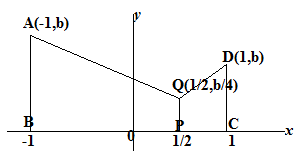
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $
$\begin{align*} A(t)&=\int_0^t bx^2 dx = \left[ \frac{b}{3}x^3 \right]_0^t = \frac{b}{3} (t^3-0^3) =\frac{b}{3} t^3 \\ t=x_0 \rightarrow A(x_0)&=\frac{b}{3} (x_0)^3 \\ t=1 \rightarrow A(1)&=\frac{b}{3} (1)^3 = \frac{b}{3} \end{align*}$
$\spadesuit \, $ Menentukan $x_0 \, $ dari $A(x_0):A(1)=1:8$
$\begin{align*} \frac{A(x_0)}{A(1)}&=\frac{1}{8} \Rightarrow \frac{\frac{b}{3} (x_0)^3}{\frac{b}{3}}=\frac{1}{8} \Rightarrow x_0^3=\frac{1}{8} \Rightarrow x_0= \frac{1}{2} \end{align*}$
$\spadesuit \, $ Menentukan titik A, Q, dan D dengan menggunakan $y=bx^2$
titik A : $x=-1 \Rightarrow y=b(-1)^2 = b. \,$ Jadi titik A(-1, b)
titik Q : $x=\frac{1}{2} \Rightarrow y=b\left( \frac{1}{2} \right)^2 = b.\,$ Jadi titik Q(1/2, b/4)
titik D : $x=1 \Rightarrow y=b(1)^2 = b.\,$ Jadi titik D(1, b)
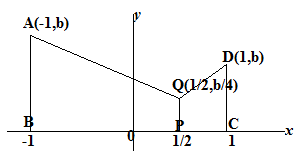
$\spadesuit \, $ Menentukan perbandingan luas $ABPQ:DCPQ$
$\frac{L.ABPQ}{L.DCPQ}=\frac{\frac{1}{2}(AB+PQ).BP}{\frac{1}{2}(CD+PQ).CP}=\frac{(b+\frac{b}{4}).\frac{3}{2}}{(b+\frac{b}{4}).\frac{1}{2}} = \frac{3}{1} $
Jadi, perbandingan luas $\frac{L.ABPQ}{L.DCPQ}=\frac{3}{1}. \, \heartsuit $


