Nomor 11
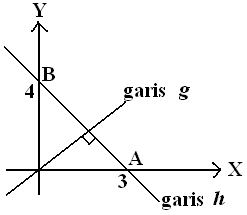
Garis $g \, $ melalui titik $(-2, -1) \, \, $ dan menyinggung kurva $ K : \, \, y = 2\sqrt{x}. \, \, $ Jika titik singgung
garis $g \, $ dan kurva $ K \, $ adalah $(a, \, b) \, $ , maka $a+b = .... $
$\spadesuit \, $ Gambar

Substitusi titik $(a,b) \, $ ke kurva
$y=2\sqrt{x} \rightarrow b = 2\sqrt{a} \rightarrow \sqrt{a} = \frac{b}{2} \rightarrow a = \frac{b^2}{4} \, \, \, $ ...pers(i)
(nilai $b \, $ positif karena $\sqrt{a} \, $ selalu positif)
$\spadesuit \, $ Gradien garis $g \, \, $ melalui titik A dan B
$m_g = \frac{y_2-y_1}{x_2-x_1} = \frac{b-(-1)}{a-(-2)} = \frac{b+1}{a+2} $
$\spadesuit \, $ Gradien garis singgung $g \, \, $ di titik B$(a,b) \, $ : $ m_g = f^\prime (a) $
$y = 2\sqrt{x} \rightarrow y^\prime = \frac{1}{\sqrt{x}} $
$ m_g = f^\prime (a) \rightarrow m_g = \frac{1}{\sqrt{a}} $
$\spadesuit \, $ Gradien sama, dan gunakan pers(i)
$\begin{align} \frac{1}{\sqrt{a}} & = \frac{b+1}{a+2} \\ \frac{1}{\frac{b}{2}} & = \frac{b+1}{\frac{b^2}{4}+2} \\ \frac{2}{b} & = \frac{b+1}{\frac{b^2}{4}+2} \\ b^2+2b-8 & = 0 \\ (b-2)(b+4) & = 0 \\ b=2 & \vee b = -4 \end{align}$
yang memenuhi $ b = 2 \, \, $ karena positif
$b = 2 \rightarrow a = \frac{b^2}{4} = \frac{2^2}{4} = 1 $
Jadi, nilai $ a + b = 1 + 2 = 3. \heartsuit $

Substitusi titik $(a,b) \, $ ke kurva
$y=2\sqrt{x} \rightarrow b = 2\sqrt{a} \rightarrow \sqrt{a} = \frac{b}{2} \rightarrow a = \frac{b^2}{4} \, \, \, $ ...pers(i)
(nilai $b \, $ positif karena $\sqrt{a} \, $ selalu positif)
$\spadesuit \, $ Gradien garis $g \, \, $ melalui titik A dan B
$m_g = \frac{y_2-y_1}{x_2-x_1} = \frac{b-(-1)}{a-(-2)} = \frac{b+1}{a+2} $
$\spadesuit \, $ Gradien garis singgung $g \, \, $ di titik B$(a,b) \, $ : $ m_g = f^\prime (a) $
$y = 2\sqrt{x} \rightarrow y^\prime = \frac{1}{\sqrt{x}} $
$ m_g = f^\prime (a) \rightarrow m_g = \frac{1}{\sqrt{a}} $
$\spadesuit \, $ Gradien sama, dan gunakan pers(i)
$\begin{align} \frac{1}{\sqrt{a}} & = \frac{b+1}{a+2} \\ \frac{1}{\frac{b}{2}} & = \frac{b+1}{\frac{b^2}{4}+2} \\ \frac{2}{b} & = \frac{b+1}{\frac{b^2}{4}+2} \\ b^2+2b-8 & = 0 \\ (b-2)(b+4) & = 0 \\ b=2 & \vee b = -4 \end{align}$
yang memenuhi $ b = 2 \, \, $ karena positif
$b = 2 \rightarrow a = \frac{b^2}{4} = \frac{2^2}{4} = 1 $
Jadi, nilai $ a + b = 1 + 2 = 3. \heartsuit $
Nomor 12
$\displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) }{\sqrt{\frac{x}{2}} - \sqrt{\frac{\pi}{4}}} = .... $
$\clubsuit \, $ Rumus dasar : $\displaystyle \lim_{x \to k } \frac{a\sin f(x)}{bf(x)} = \frac{a}{b} \, \, $ dengan $ \, f(k) = 0 $
$\clubsuit \, $ Merasionalkan penyebut
$\begin{align} \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) }{\sqrt{\frac{x}{2}} - \sqrt{\frac{\pi}{4}}} & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) }{\sqrt{\frac{x}{2}} - \sqrt{\frac{\pi}{4}}} . \frac{\sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}}}{\sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}}} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) . \left( \sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{x}{2} - \frac{\pi}{4}} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\left( \sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{1}{2}} . \frac{\sin \left( x - \frac{\pi}{2} \right)}{\left( x - \frac{\pi}{2} \right)} \\ & = \frac{\left( \sqrt{\frac{\frac{\pi}{2}}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{1}{2}} . \frac{1}{1} \\ & = 2 \left( 2 \sqrt{\frac{\pi}{4}} \right) = 2\sqrt{\pi} \end{align}$
Jadi, nilai limitnya adalah $ 2\sqrt{\pi} . \heartsuit $
$\clubsuit \, $ Merasionalkan penyebut
$\begin{align} \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) }{\sqrt{\frac{x}{2}} - \sqrt{\frac{\pi}{4}}} & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) }{\sqrt{\frac{x}{2}} - \sqrt{\frac{\pi}{4}}} . \frac{\sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}}}{\sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}}} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\sin \left( x - \frac{\pi}{2} \right) . \left( \sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{x}{2} - \frac{\pi}{4}} \\ & = \displaystyle \lim_{x \to \frac{\pi}{2} } \frac{\left( \sqrt{\frac{x}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{1}{2}} . \frac{\sin \left( x - \frac{\pi}{2} \right)}{\left( x - \frac{\pi}{2} \right)} \\ & = \frac{\left( \sqrt{\frac{\frac{\pi}{2}}{2}} + \sqrt{\frac{\pi}{4}} \right)}{\frac{1}{2}} . \frac{1}{1} \\ & = 2 \left( 2 \sqrt{\frac{\pi}{4}} \right) = 2\sqrt{\pi} \end{align}$
Jadi, nilai limitnya adalah $ 2\sqrt{\pi} . \heartsuit $
Nomor 13
Jika BC = CD, maka $\cos B = .... $
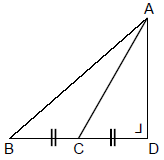

$\spadesuit \, $ Segitiga ACD
$\tan x = \frac{AD}{CD} \rightarrow AD = CD. \tan x $
$\spadesuit \, $ Segitiga ABC
$\tan B = \frac{AD}{BD} = \frac{CD. \tan x}{2.CD} = \frac{\tan x}{2} $

Jadi, nilai $ \cos B = \frac{2}{\sqrt{4+\tan ^2 x}} . \heartsuit $
$\tan x = \frac{AD}{CD} \rightarrow AD = CD. \tan x $
$\spadesuit \, $ Segitiga ABC
$\tan B = \frac{AD}{BD} = \frac{CD. \tan x}{2.CD} = \frac{\tan x}{2} $

Jadi, nilai $ \cos B = \frac{2}{\sqrt{4+\tan ^2 x}} . \heartsuit $
Nomor 14
Grafik fungsi $f(x) = x\sqrt{x-2} \, \, $ naik untuk nilai $x \, $ yang memenuhi .....
$\clubsuit \,$ Konsep turunan : $ f = U.V \rightarrow f^\prime = U^\prime . V + U . V^\prime $
$\clubsuit \,$ Menentukan turunan $f(x)$
$f(x) = x\sqrt{x-2} \rightarrow f^\prime (x) = \sqrt{x-2} + x. \frac{1}{2\sqrt{x-2}} $
$f^\prime (x) = \frac{3x-4}{2\sqrt{x-2}} $
$\clubsuit \,$ Syarat fungsi naik : $ f^\prime (x) > 0 $
$ f^\prime (x) > 0 \rightarrow \frac{3x-4}{2\sqrt{x-2}} > 0 $
$ x = \frac{4}{3} \vee x = 2 $
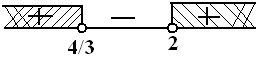
$HP_1 = \{ x < \frac{4}{3} \vee x > 2 \} $
$\clubsuit \,$ Syarat akar
$ \sqrt{x-2} \geq 0 \rightarrow x - 2 \geq 0 \rightarrow x \geq 2 \, \, \, $ ...(HP2)
sehingga, $ HP = HP_1 \cap HP_2 = \{ x > 2 \} $
Jadi, fungsi naik pada interval $ \{ x > 2 \} . \heartsuit $
$\clubsuit \,$ Menentukan turunan $f(x)$
$f(x) = x\sqrt{x-2} \rightarrow f^\prime (x) = \sqrt{x-2} + x. \frac{1}{2\sqrt{x-2}} $
$f^\prime (x) = \frac{3x-4}{2\sqrt{x-2}} $
$\clubsuit \,$ Syarat fungsi naik : $ f^\prime (x) > 0 $
$ f^\prime (x) > 0 \rightarrow \frac{3x-4}{2\sqrt{x-2}} > 0 $
$ x = \frac{4}{3} \vee x = 2 $
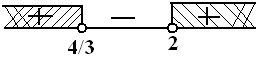
$HP_1 = \{ x < \frac{4}{3} \vee x > 2 \} $
$\clubsuit \,$ Syarat akar
$ \sqrt{x-2} \geq 0 \rightarrow x - 2 \geq 0 \rightarrow x \geq 2 \, \, \, $ ...(HP2)
sehingga, $ HP = HP_1 \cap HP_2 = \{ x > 2 \} $
Jadi, fungsi naik pada interval $ \{ x > 2 \} . \heartsuit $
Nomor 15
Nilai $x \, $ yang memenuhi persamaan : $\left( {}^4 \log x \right)^2 - {}^2 \log \sqrt{x} - \frac{3}{4} = 0 \, \, $
adalah ....
$\spadesuit \, $ Sifat logaritma : $ {{}^a}^n \log b^n = {}^a \log b $
Misalkan : $ p = {}^4 \log x $
$\spadesuit \, $ Menyederhanakan bentuk log
$\begin{align} \left( {}^4 \log x \right)^2 - {}^2 \log \sqrt{x} - \frac{3}{4} & = 0 \\ \left( {}^4 \log x \right)^2 - {{}^2}^2 \log (\sqrt{x})^2 - \frac{3}{4} & = 0 \\ \left( {}^4 \log x \right)^2 - {}^4 \log x - \frac{3}{4} & = 0 \\ p^2 - p - \frac{3}{4} & = 0 \, \, \text{(kali 4)} \\ 4p^2 - 4p - 3 & = 0 \\ (2p+1)(2p-3) & = 0 \\ p=-\frac{1}{2} \rightarrow & \, \, {}^4 \log x = -\frac{1}{2} \rightarrow x = (4)^{-\frac{1}{2}} = \frac{1}{2} \\ p=\frac{3}{2} \rightarrow & \, \, {}^4 \log x = \frac{3}{2} \rightarrow x = (4)^\frac{3}{2} = 8 \end{align}$
Jadi, nilai $x \, $ yang memenuhi adalah 8 dan $ \frac{1}{2} . \heartsuit $
Misalkan : $ p = {}^4 \log x $
$\spadesuit \, $ Menyederhanakan bentuk log
$\begin{align} \left( {}^4 \log x \right)^2 - {}^2 \log \sqrt{x} - \frac{3}{4} & = 0 \\ \left( {}^4 \log x \right)^2 - {{}^2}^2 \log (\sqrt{x})^2 - \frac{3}{4} & = 0 \\ \left( {}^4 \log x \right)^2 - {}^4 \log x - \frac{3}{4} & = 0 \\ p^2 - p - \frac{3}{4} & = 0 \, \, \text{(kali 4)} \\ 4p^2 - 4p - 3 & = 0 \\ (2p+1)(2p-3) & = 0 \\ p=-\frac{1}{2} \rightarrow & \, \, {}^4 \log x = -\frac{1}{2} \rightarrow x = (4)^{-\frac{1}{2}} = \frac{1}{2} \\ p=\frac{3}{2} \rightarrow & \, \, {}^4 \log x = \frac{3}{2} \rightarrow x = (4)^\frac{3}{2} = 8 \end{align}$
Jadi, nilai $x \, $ yang memenuhi adalah 8 dan $ \frac{1}{2} . \heartsuit $