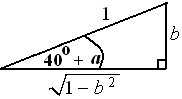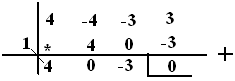Nomor 11
Suatu pin ATM terdiri dari tiga angka berbeda, tetapi angka pertama tidak boleh nol. Peluang bahwa kartu ATM tersebut mempunyai
nomor cantik 123, 234, 345, 567, 678, atau 789 adalah ....
$\spadesuit \, $ Pilihan angka dari 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 . Ada 10 pilihan angka untuk pembuatan pin ATM
Pin terdiri dari 3 angka yang berbeda ( angka yang sudah dipakai tidak boleh dipakai lagi) dan angka pertama tidak boleh nol, sehingga banyak cara penyusunannya :
Angka pertama : ada 9 pilihan angka (karena nol tidak boleh)
Angka kedua : ada 9 pilihan angka (karena satu angka sudah dipakai pada angka pertama)
Angka ketiga : ada 8 pilihan angka (karena dua angka sudah dipakai untuk angka pertama dan kedua)
sehingga total cara : $ n(S) = 9 . 9 . 8 $
$\spadesuit \, $ Angka cantiknya ada 6 yaitu : 123, 234, 345, 567, 678, atau 789
Sehingga $ n(A) = 6 \, $ (banyak harapannya)
$\spadesuit \, $ Menentukan peluangnya
$P(A)=\frac{n(A)}{n(S)}=\frac{6}{9.9.8}=\frac{3}{324}$
Jadi, peluang nomor cantiknya adalah $\frac{3}{324}. \heartsuit $
Pin terdiri dari 3 angka yang berbeda ( angka yang sudah dipakai tidak boleh dipakai lagi) dan angka pertama tidak boleh nol, sehingga banyak cara penyusunannya :
Angka pertama : ada 9 pilihan angka (karena nol tidak boleh)
Angka kedua : ada 9 pilihan angka (karena satu angka sudah dipakai pada angka pertama)
Angka ketiga : ada 8 pilihan angka (karena dua angka sudah dipakai untuk angka pertama dan kedua)
sehingga total cara : $ n(S) = 9 . 9 . 8 $
$\spadesuit \, $ Angka cantiknya ada 6 yaitu : 123, 234, 345, 567, 678, atau 789
Sehingga $ n(A) = 6 \, $ (banyak harapannya)
$\spadesuit \, $ Menentukan peluangnya
$P(A)=\frac{n(A)}{n(S)}=\frac{6}{9.9.8}=\frac{3}{324}$
Jadi, peluang nomor cantiknya adalah $\frac{3}{324}. \heartsuit $
Nomor 12
Jika $ f(x) = \frac{ax+1}{3x-1}, \, g(x) = x-2, \, $ dan $ (g^{-1} \circ f^{-1})(2) = \frac{7}{2}, \, $ maka $ a = .... $
$\clubsuit \, $ Konsep invers pada komposisi fungsi
sifat : $(f\circ g)^{-1} (x) = (g^{-1} \circ f^{-1} ) (x) $
Definisi : $ f^{-1} (x) = y \leftrightarrow x = f(y) $
$\clubsuit \, $ Menentukan nilai $ a $
$ g(x) = x-2 \rightarrow g(\frac{7}{2} ) = \frac{7}{2} - 2 \rightarrow g(\frac{7}{2} ) = \frac{3}{2} $
$\begin{align} (g^{-1} \circ f^{-1})(2) & = \frac{7}{2} \, \, \, \text{(dari sifat)} \\ (f\circ g)^{-1} (2) & = \frac{7}{2} \, \, \, \text{(dari definisi)} \\ 2 & = (f\circ g) \left( \frac{7}{2} \right) \\ 2 & = f\left( g \left( \frac{7}{2} \right) \right) \\ 2 & = f\left( \frac{3}{2} \right) \\ 2 & = \frac{a.\frac{3}{2} +1}{3.\frac{3}{2} -1} \\ 2 & = \frac{a.\frac{3}{2} +1}{3.\frac{3}{2} -1} . \frac{2}{2} \\ 2 & = \frac{3a +2}{9-2} \\ 2 & = \frac{3a +2}{7} \\ 3a + 2 & = 14 \\ 3a & = 12 \\ a & = 4 \end{align}$
Jadi, nilai $ a = 4. \heartsuit $
sifat : $(f\circ g)^{-1} (x) = (g^{-1} \circ f^{-1} ) (x) $
Definisi : $ f^{-1} (x) = y \leftrightarrow x = f(y) $
$\clubsuit \, $ Menentukan nilai $ a $
$ g(x) = x-2 \rightarrow g(\frac{7}{2} ) = \frac{7}{2} - 2 \rightarrow g(\frac{7}{2} ) = \frac{3}{2} $
$\begin{align} (g^{-1} \circ f^{-1})(2) & = \frac{7}{2} \, \, \, \text{(dari sifat)} \\ (f\circ g)^{-1} (2) & = \frac{7}{2} \, \, \, \text{(dari definisi)} \\ 2 & = (f\circ g) \left( \frac{7}{2} \right) \\ 2 & = f\left( g \left( \frac{7}{2} \right) \right) \\ 2 & = f\left( \frac{3}{2} \right) \\ 2 & = \frac{a.\frac{3}{2} +1}{3.\frac{3}{2} -1} \\ 2 & = \frac{a.\frac{3}{2} +1}{3.\frac{3}{2} -1} . \frac{2}{2} \\ 2 & = \frac{3a +2}{9-2} \\ 2 & = \frac{3a +2}{7} \\ 3a + 2 & = 14 \\ 3a & = 12 \\ a & = 4 \end{align}$
Jadi, nilai $ a = 4. \heartsuit $
Nomor 13
Syarat agar fungsi $ f(x) = -x^3 + \frac{1}{2}ax^2 - \frac{1}{2}x^2 - 3x + 8 \, $ selalu turun untuk semua nilai real $ x \, $ adalah ....
$\spadesuit \, $ Konsep dasar
Fungsi $ f(x) $ akan turun dengan syarat : $ f^\prime (x) < 0 $
Suatu fungsi kuadrat disebut definit negatif (nilainya akan selalu negatif untuk semua $ x \, $ ) jika memenuhi syarat : $ a < 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Menentukan turunan fungsi $ f(x) = -x^3 + \frac{1}{2}ax^2 - \frac{1}{2}x^2 - 3x + 8 $
$\begin{align} \text{turunannya : } \, f^\prime (x) & = -3x^2 + ax - x - 3 \\ f^\prime (x) & = -3x^2 + (a-1)x - 3 \end{align}$
$\begin{align} \text{Syarat turun : } \, \, \, \, f^\prime (x) & < 0 \\ -3x^2 + (a-1)x - 3 & < 0 \end{align}$
$\spadesuit \, $ Bentuk $ -3x^2 + (a-1)x - 3 < 0 \, $ artinya nilai $ -3x^2 + (a-1)x - 3 \, $ selalu negatif untuk semua $ x \, $ yang terpenuhi untuk syarat definit negatif : $ a < 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Menyelesaikan syarat definit negatif dari $ -3x^2 + (a-1)x - 3 $
syarat(i) : $ a < 0 \rightarrow -3 < 0 \, $ (benar)
$\begin{align} \text{syarat(ii) : } \, D < 0 \rightarrow b^2 - 4ac & < 0 \\ (a-1)^2 - 4.(-3).(-3) & < 0 \\ a^2 - 2a + 1 - 36 & < 0 \\ a^2 - 2a - 35 & < 0 \\ (a +5)(a-7) & < 0 \\ a = -5 \vee a & = 7 \end{align}$

Jadi, solusinya HP $ = \{ -5 < a < 7 \} . \heartsuit $
Fungsi $ f(x) $ akan turun dengan syarat : $ f^\prime (x) < 0 $
Suatu fungsi kuadrat disebut definit negatif (nilainya akan selalu negatif untuk semua $ x \, $ ) jika memenuhi syarat : $ a < 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Menentukan turunan fungsi $ f(x) = -x^3 + \frac{1}{2}ax^2 - \frac{1}{2}x^2 - 3x + 8 $
$\begin{align} \text{turunannya : } \, f^\prime (x) & = -3x^2 + ax - x - 3 \\ f^\prime (x) & = -3x^2 + (a-1)x - 3 \end{align}$
$\begin{align} \text{Syarat turun : } \, \, \, \, f^\prime (x) & < 0 \\ -3x^2 + (a-1)x - 3 & < 0 \end{align}$
$\spadesuit \, $ Bentuk $ -3x^2 + (a-1)x - 3 < 0 \, $ artinya nilai $ -3x^2 + (a-1)x - 3 \, $ selalu negatif untuk semua $ x \, $ yang terpenuhi untuk syarat definit negatif : $ a < 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Menyelesaikan syarat definit negatif dari $ -3x^2 + (a-1)x - 3 $
syarat(i) : $ a < 0 \rightarrow -3 < 0 \, $ (benar)
$\begin{align} \text{syarat(ii) : } \, D < 0 \rightarrow b^2 - 4ac & < 0 \\ (a-1)^2 - 4.(-3).(-3) & < 0 \\ a^2 - 2a + 1 - 36 & < 0 \\ a^2 - 2a - 35 & < 0 \\ (a +5)(a-7) & < 0 \\ a = -5 \vee a & = 7 \end{align}$

Jadi, solusinya HP $ = \{ -5 < a < 7 \} . \heartsuit $
Nomor 14
Himpunan penyelesaian dari $ \left( \frac{1}{8} \right)^{8+2x-x^2} \geq \left( \frac{1}{16} \right)^{x+2} \, $ adalah ....
$\clubsuit \, $ Konsep pertidaksamaan eksponen (perpangkatan)
$ a^{f(x)} \geq a^{g(x)} \, \text{solusinya} \, \left\{ \begin{array}{cc} f(x) \geq g(x) , & \text{untuk} \, a > 1 \\ f(x) \leq g(x), & \text{untuk} \, 0 < a < 1 \end{array} \right. $
Sifat eksponen : $ (a^m)^n = a^{m.n} $
$\clubsuit \, $ Menyamakan basis
$\begin{align} \left( \frac{1}{8} \right)^{8+2x-x^2} & \geq \left( \frac{1}{16} \right)^{x+2} \\ \left( \left( \frac{1}{2} \right)^3 \right)^{8+2x-x^2} & \geq \left( \left( \frac{1}{2} \right)^4 \right)^{x+2} \\ \left( \frac{1}{2} \right)^{24+6x-3x^2} & \geq \left( \frac{1}{2} \right)^{4x+8} \\ 24+6x-3x^2 & \leq 4x+8 \, \, \, \text{(dibalik karena basis kurang dari 1)} \\ -3x^2 + 2x + 16 & \leq 0 \, \, \, \text{(kali -1, tanda dibalik)} \\ 3x^2 - 2x - 16 & \geq 0 \\ (3x-8)(x+2) & \geq 0 \\ x = \frac{8}{3} \vee x & = -2 \end{align} $
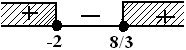
Jadi, $HP = \{ x \leq -2 \vee x \geq \frac{8}{3} \} . \heartsuit $
$ a^{f(x)} \geq a^{g(x)} \, \text{solusinya} \, \left\{ \begin{array}{cc} f(x) \geq g(x) , & \text{untuk} \, a > 1 \\ f(x) \leq g(x), & \text{untuk} \, 0 < a < 1 \end{array} \right. $
Sifat eksponen : $ (a^m)^n = a^{m.n} $
$\clubsuit \, $ Menyamakan basis
$\begin{align} \left( \frac{1}{8} \right)^{8+2x-x^2} & \geq \left( \frac{1}{16} \right)^{x+2} \\ \left( \left( \frac{1}{2} \right)^3 \right)^{8+2x-x^2} & \geq \left( \left( \frac{1}{2} \right)^4 \right)^{x+2} \\ \left( \frac{1}{2} \right)^{24+6x-3x^2} & \geq \left( \frac{1}{2} \right)^{4x+8} \\ 24+6x-3x^2 & \leq 4x+8 \, \, \, \text{(dibalik karena basis kurang dari 1)} \\ -3x^2 + 2x + 16 & \leq 0 \, \, \, \text{(kali -1, tanda dibalik)} \\ 3x^2 - 2x - 16 & \geq 0 \\ (3x-8)(x+2) & \geq 0 \\ x = \frac{8}{3} \vee x & = -2 \end{align} $
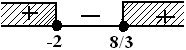
Jadi, $HP = \{ x \leq -2 \vee x \geq \frac{8}{3} \} . \heartsuit $
Nomor 15
Jika $ \log (\log x ) = \log (\log (1+y)) + \log 2 \, $ dan $ \log (x-5) = 2\log y , \, $ maka $ x + y = ..... $
$\clubsuit \, $ Konsep logaritma
Persamaan : $ {}^a \log f(x) = {}^a \log g(x) \rightarrow f(x) = g(x) $
Sifat-sifat logaritma :
$ {}^a \log b + {}^a \log c = {}^a \log (bc) $
$ {}^a \log b^n = n.{}^a \log b $
$\clubsuit \, $ Menyederhanakan kedua persamaan
Persamaan pertama :
$\begin{align} \log (\log x ) & = \log (\log (1+y)) + \log 2 \, \, \, \text{(dengan sifat log)} \\ \log (\log x ) & = \log [(\log (1+y)) . 2 ] \\ \log (\log x ) & = \log [2.\log (1+y) ] \, \, \, \text{(coret log paling luar)} \\ \log x & = 2.\log (1+y) \\ \log x & = \log (1+y)^2 \, \, \, \text{(coret log)} \\ x & = (1+y)^2 \\ x & = y^2 + 2y + 1 \, \, \, \text{...pers(i)} \end{align} $
Persamaan kedua :
$\begin{align} \log (x-5) & = 2\log y \\ \log (x-5) & = \log y^2 \, \, \, \text{(coret log)} \\ x - 5 & = y^2 \, \, \, \text{...pers(ii)} \end{align} $
$\clubsuit \, $ Sustitusi pers(i) ke pers(ii)
$\begin{align} x - 5 & = y^2 \\ y^2 + 2y + 1 - 5 & = y^2 \\ 2y & = 4 \\ y & = 2 \end{align} $
pers(ii) : $ x-5 = y^2 \rightarrow x-5 = 2^2 \rightarrow x = 9 $
sehingga nilai $ x + y = 9 + 2 = 11 $
Jadi, nilai $ x + y = 11 . \heartsuit $
Persamaan : $ {}^a \log f(x) = {}^a \log g(x) \rightarrow f(x) = g(x) $
Sifat-sifat logaritma :
$ {}^a \log b + {}^a \log c = {}^a \log (bc) $
$ {}^a \log b^n = n.{}^a \log b $
$\clubsuit \, $ Menyederhanakan kedua persamaan
Persamaan pertama :
$\begin{align} \log (\log x ) & = \log (\log (1+y)) + \log 2 \, \, \, \text{(dengan sifat log)} \\ \log (\log x ) & = \log [(\log (1+y)) . 2 ] \\ \log (\log x ) & = \log [2.\log (1+y) ] \, \, \, \text{(coret log paling luar)} \\ \log x & = 2.\log (1+y) \\ \log x & = \log (1+y)^2 \, \, \, \text{(coret log)} \\ x & = (1+y)^2 \\ x & = y^2 + 2y + 1 \, \, \, \text{...pers(i)} \end{align} $
Persamaan kedua :
$\begin{align} \log (x-5) & = 2\log y \\ \log (x-5) & = \log y^2 \, \, \, \text{(coret log)} \\ x - 5 & = y^2 \, \, \, \text{...pers(ii)} \end{align} $
$\clubsuit \, $ Sustitusi pers(i) ke pers(ii)
$\begin{align} x - 5 & = y^2 \\ y^2 + 2y + 1 - 5 & = y^2 \\ 2y & = 4 \\ y & = 2 \end{align} $
pers(ii) : $ x-5 = y^2 \rightarrow x-5 = 2^2 \rightarrow x = 9 $
sehingga nilai $ x + y = 9 + 2 = 11 $
Jadi, nilai $ x + y = 11 . \heartsuit $