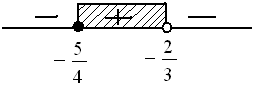
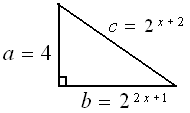Nomor 21
Dari sehelai karton akan dibuat sebuah kotak tanpa tutup dengan alas bujur sangkar. Jika jumlah luas bidang alas dan semua bidang sisi
kotak ditentukan sebesar 432 cm$^2\, $ , maka volume kotak terbesar yang mungkin adalah ....
$\spadesuit \, $ Gambar
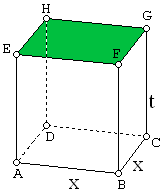
$\begin{align} L_p & = L_{alas} + 4\times L_{samping} \\ 432 & = x^2 + 4xt \\ t & = \frac{432 - x^2}{4x} \end{align}$
$\spadesuit \, $ Menentukan volume dan turunannya
$\begin{align} V & = L_{alas} \times t \\ V & = x^2.t \\ V & = x^2 . \frac{432 - x^2}{4x} \\ V & = \frac{1}{4} (432x-x^3) \rightarrow V^\prime = \frac{1}{4}(432-3x^2) \end{align}$
$\spadesuit \, $ Nilai max/min : $ V^\prime = 0 \, $ (turunan = 0)
$ V^\prime = 0 \rightarrow \frac{1}{4}(432-3x^2) = 0 \rightarrow x = 12 $
sehingga volume maksimumnya saat $ x = 12 $
$V_{max} = \frac{1}{4} (432x-x^3) = \frac{1}{4} (432.12-(12)^3) = 864 $
Jadi, volume maksimumnya adalah 864. $ \heartsuit $

$\begin{align} L_p & = L_{alas} + 4\times L_{samping} \\ 432 & = x^2 + 4xt \\ t & = \frac{432 - x^2}{4x} \end{align}$
$\spadesuit \, $ Menentukan volume dan turunannya
$\begin{align} V & = L_{alas} \times t \\ V & = x^2.t \\ V & = x^2 . \frac{432 - x^2}{4x} \\ V & = \frac{1}{4} (432x-x^3) \rightarrow V^\prime = \frac{1}{4}(432-3x^2) \end{align}$
$\spadesuit \, $ Nilai max/min : $ V^\prime = 0 \, $ (turunan = 0)
$ V^\prime = 0 \rightarrow \frac{1}{4}(432-3x^2) = 0 \rightarrow x = 12 $
sehingga volume maksimumnya saat $ x = 12 $
$V_{max} = \frac{1}{4} (432x-x^3) = \frac{1}{4} (432.12-(12)^3) = 864 $
Jadi, volume maksimumnya adalah 864. $ \heartsuit $
Cara II
$\spadesuit \, $ Balok tanpa tutup :
$V_{max} = \frac{L_p}{6}.\sqrt{\frac{L_p}{3}} $
$\spadesuit \, $ Menentukan volume maksimum dengan $ L_p = 432 $
$V_{max} = \frac{L_p}{6}.\sqrt{\frac{L_p}{3}} = \frac{432}{6}.\sqrt{\frac{432}{3}} = 864 $
Jadi, volume maksimumnya adalah 864. $ \heartsuit $
$\spadesuit \, $ Balok tanpa tutup :
$V_{max} = \frac{L_p}{6}.\sqrt{\frac{L_p}{3}} $
$\spadesuit \, $ Menentukan volume maksimum dengan $ L_p = 432 $
$V_{max} = \frac{L_p}{6}.\sqrt{\frac{L_p}{3}} = \frac{432}{6}.\sqrt{\frac{432}{3}} = 864 $
Jadi, volume maksimumnya adalah 864. $ \heartsuit $
Nomor 22
Jika $r \, $ rasio deret geometri tak hingga yang jumlahnya mempunyai limit dan $S \, $ limit jumlah deret tak hingga
$1 + \frac{1}{4+r} + \frac{1}{(4+r)^2} + ....+ \frac{1}{(4+r)^n} + ..... \, $ , maka .....
$\clubsuit \, r \, $ adalah rasio deret geometri tak hingga, sehingga harus $ -1 < r < 1 $
Rumus dasar tak hingga : $ S_\infty = \frac{a}{1-rasio} $
Deret : $1 + \frac{1}{4+r} + \frac{1}{(4+r)^2} + ....+ \frac{1}{(4+r)^n} + ..... \, $
dengan $ a = 1 \, \, $ dan $ \, rasio = \frac{U_2}{U_1} = \frac{1}{4+r} $
Jumlah tak hingganya dengan $S_\infty = S $ adalah :
$\begin{align} S_\infty & = \frac{a}{1-rasio} \\ S & = \frac{1}{1- \frac{1}{4+r} } \\ S & = \frac{4+r}{3+r} \\ S & = 1 + \frac{1}{3+r} \end{align}$
Untuk interval nilai $ r $ : $ -1 < r < 1 $
Nilai terkecil untuk $r=1 $ , $ S = 1 + \frac{1}{3+1} = 1\frac{1}{4} $
Nilai terbesar untuk $r=-1 $ , $ S = 1 + \frac{1}{3+(-1)} = 1\frac{1}{2} $
Jadi, rentang nilai $ S $ adalah $ 1\frac{1}{4} < S < 1\frac{1}{2}. \heartsuit $
Rumus dasar tak hingga : $ S_\infty = \frac{a}{1-rasio} $
Deret : $1 + \frac{1}{4+r} + \frac{1}{(4+r)^2} + ....+ \frac{1}{(4+r)^n} + ..... \, $
dengan $ a = 1 \, \, $ dan $ \, rasio = \frac{U_2}{U_1} = \frac{1}{4+r} $
Jumlah tak hingganya dengan $S_\infty = S $ adalah :
$\begin{align} S_\infty & = \frac{a}{1-rasio} \\ S & = \frac{1}{1- \frac{1}{4+r} } \\ S & = \frac{4+r}{3+r} \\ S & = 1 + \frac{1}{3+r} \end{align}$
Untuk interval nilai $ r $ : $ -1 < r < 1 $
Nilai terkecil untuk $r=1 $ , $ S = 1 + \frac{1}{3+1} = 1\frac{1}{4} $
Nilai terbesar untuk $r=-1 $ , $ S = 1 + \frac{1}{3+(-1)} = 1\frac{1}{2} $
Jadi, rentang nilai $ S $ adalah $ 1\frac{1}{4} < S < 1\frac{1}{2}. \heartsuit $
Nomor 23
Titik-titik sudut segitiga sama kaki ABC terletak pada lingkaran berjari-jari 3 cm. Jika alas AB = $2\sqrt{2} \, $ cm, maka
$\, \, \tan A = .... $
$\spadesuit \, $ Gambar
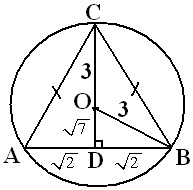
$AB = 2\sqrt{2} \rightarrow AD = \frac{1}{2}AB = \sqrt{2} $
$OD = \sqrt{OB^2-DB^2} = \sqrt{3^2 - \sqrt{2}^2} = \sqrt{9-2} = \sqrt{7} $
$CD = CO + OD = 3 + \sqrt{7} $
$\spadesuit \, $ Menentukan nilai tan A pada segitiga ACD
$\begin{align} \tan A & = \frac{CD}{AD} = \frac{3+\sqrt{7}}{\sqrt{2}} \\ & = \frac{3+\sqrt{7}}{\sqrt{2}} . \frac{\sqrt{2}}{\sqrt{2}} \\ \tan A & = \frac{1}{2}(3\sqrt{2}+\sqrt{14}) \end{align}$
Jadi, nilai $ \tan A = \frac{1}{2}(3\sqrt{2}+\sqrt{14}) . \heartsuit $

$AB = 2\sqrt{2} \rightarrow AD = \frac{1}{2}AB = \sqrt{2} $
$OD = \sqrt{OB^2-DB^2} = \sqrt{3^2 - \sqrt{2}^2} = \sqrt{9-2} = \sqrt{7} $
$CD = CO + OD = 3 + \sqrt{7} $
$\spadesuit \, $ Menentukan nilai tan A pada segitiga ACD
$\begin{align} \tan A & = \frac{CD}{AD} = \frac{3+\sqrt{7}}{\sqrt{2}} \\ & = \frac{3+\sqrt{7}}{\sqrt{2}} . \frac{\sqrt{2}}{\sqrt{2}} \\ \tan A & = \frac{1}{2}(3\sqrt{2}+\sqrt{14}) \end{align}$
Jadi, nilai $ \tan A = \frac{1}{2}(3\sqrt{2}+\sqrt{14}) . \heartsuit $
Nomor 24
Jika ${}^8 \log 5 = r , \, $ maka $ \, {}^5 \log 16 = .... $
$\clubsuit \,$ Sifat-sifat logaritma
${{}^a}^m \log b^n = \frac{n}{m} {}^a \log b \, \, $ dan $ \, {}^a \log b = \frac{1}{{}^b \log a} $
$\clubsuit \,$ Menyederhanakan yang diketahui
${}^8 \log 5 = r \rightarrow {{}^2}^3 \log 5^1 = r $
$ \rightarrow \frac{1}{3} {}^2 \log 5 = r \rightarrow {}^2 \log 5 = 3r $
$\clubsuit \,$ Menyelesaikan soal
$\begin{align} {}^5 \log 16 & = {}^5 \log 2^4 \\ & = 4 . {}^5 \log 2 \\ & = 4. \frac{1}{{}^2 \log 5} \\ & = 4 . \frac{1}{3r} = \frac{4}{3r} \end{align}$
Jadi, nilai $ {}^5 \log 16 = \frac{4}{3r} . \heartsuit $
${{}^a}^m \log b^n = \frac{n}{m} {}^a \log b \, \, $ dan $ \, {}^a \log b = \frac{1}{{}^b \log a} $
$\clubsuit \,$ Menyederhanakan yang diketahui
${}^8 \log 5 = r \rightarrow {{}^2}^3 \log 5^1 = r $
$ \rightarrow \frac{1}{3} {}^2 \log 5 = r \rightarrow {}^2 \log 5 = 3r $
$\clubsuit \,$ Menyelesaikan soal
$\begin{align} {}^5 \log 16 & = {}^5 \log 2^4 \\ & = 4 . {}^5 \log 2 \\ & = 4. \frac{1}{{}^2 \log 5} \\ & = 4 . \frac{1}{3r} = \frac{4}{3r} \end{align}$
Jadi, nilai $ {}^5 \log 16 = \frac{4}{3r} . \heartsuit $
Nomor 25
Untuk memperpendek lintasan A menuju C melalui B, dibuat jalan pintas dari A langsung ke C. Jika AB = $a \, $ dan BC = $3a \, $ ,
maka panjang jalur pintas AC adalah .....
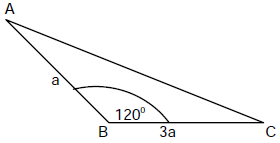

$\spadesuit \, $ Aturan cosinus pada sudut B
$\begin{align} AC^2 & = BC^2 + BA^2 - 2BC.BA . \cos B \\ & = (3a)^2 + a^2 - 2 . (3a).a . \cos 120^\circ \\ & = 9a^2 + a^2 - 6a^2. (-\frac{1}{2}) \\ & = 10a^2 + 3a^2 \\ AC^2 & = 13a^2 \\ AC & = \sqrt{13a^2} = a\sqrt{13} \end{align}$
Jadi, panajang $ AC = a\sqrt{13} . \heartsuit $
$\begin{align} AC^2 & = BC^2 + BA^2 - 2BC.BA . \cos B \\ & = (3a)^2 + a^2 - 2 . (3a).a . \cos 120^\circ \\ & = 9a^2 + a^2 - 6a^2. (-\frac{1}{2}) \\ & = 10a^2 + 3a^2 \\ AC^2 & = 13a^2 \\ AC & = \sqrt{13a^2} = a\sqrt{13} \end{align}$
Jadi, panajang $ AC = a\sqrt{13} . \heartsuit $