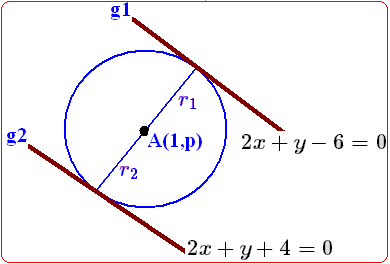
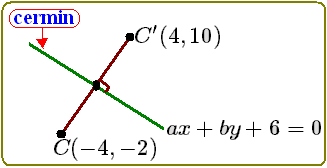
Nomor 6
Jika $ x_1 \, $ dan $ x_2 \, $ memenuhi $ |3x-4| = x+5 , \, $ maka nilai $ x_1+x_2 \, $ adalah ....
$\spadesuit \, $ Konsep Dasar :
*). Konsep harga mutlak : $|f(x)|^2 = [f(x)]^2 $
*). Penjumlahan akar-akar dari PK : $ ax^2 + bx + c = 0 $
$ x_1 + x_2 = -\frac{b}{a} $
$\spadesuit \, $ Kuadratkan persamaan :
$\begin{align} |3x-4| & = x+5 \\ |3x-4|^2 & = (x+5)^2 \\ (3x-4)^2 & = (x+5)^2 \\ 9x^2 - 24x + 16 & = x^2 + 10x + 25 \\ 8x^2 - 34x -9 & = 0 \\ x_1 + x_2 & = -\frac{b}{a} \\ & = - \frac{-34}{8} = \frac{17}{4} \end{align}$
Jadi, nilai $ x_1 + x_2 = \frac{17}{4} . \, \heartsuit $
*). Konsep harga mutlak : $|f(x)|^2 = [f(x)]^2 $
*). Penjumlahan akar-akar dari PK : $ ax^2 + bx + c = 0 $
$ x_1 + x_2 = -\frac{b}{a} $
$\spadesuit \, $ Kuadratkan persamaan :
$\begin{align} |3x-4| & = x+5 \\ |3x-4|^2 & = (x+5)^2 \\ (3x-4)^2 & = (x+5)^2 \\ 9x^2 - 24x + 16 & = x^2 + 10x + 25 \\ 8x^2 - 34x -9 & = 0 \\ x_1 + x_2 & = -\frac{b}{a} \\ & = - \frac{-34}{8} = \frac{17}{4} \end{align}$
Jadi, nilai $ x_1 + x_2 = \frac{17}{4} . \, \heartsuit $
Nomor 7
Jika 9, $ x_1 , \, $ dan $ x_2 \, $ merupakan tiga akar berbeda dari $ x^3 - 6x^2 - ax + b = 0 \, $ dengan $ b - a = 5, \, $
maka $ x_1 + x_2 + x_1.x_2 = .... $
$\clubsuit \, $ Operasi akar-akar pada $ ax^3 + bx^2 + cx + d = 0 $
$ x_1 + x_2 + x_3 = -\frac{b}{a} \, $ dan $ x_1 . x_2 . x_3 = -\frac{d}{a} $.
$\clubsuit \, $ Substitusi $x=9 $ ke persamaan
$\begin{align} x = 9 \rightarrow x^3 - 6x^2 - ax + b & = 0 \\ 9^3 - 6.9^2 - a.9 + b & = 0 \\ - 9a + b & = -243 \, \, \, \, \, \text{...pers(i)} \end{align}$
Sebelumnya diketahui : $ b - a = 5 \, $ ....pers(ii).
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} - 9a + b = -243 & \\ b - a = 5 & - \\ \hline -8a = - 248 & \\ a = 31 & \end{array}$
Pers(ii) : $ b - a = 5 \rightarrow b - 31 = 5 \rightarrow b = 36 $.
Persamaannya menjadi :
$ x^3 - 6x^2 - ax + b = 0 \rightarrow x^3 - 6x^2 - 31x + 36 = 0 $
$\clubsuit \, $ Operasi akar-akar persamaan :
Dari persamaan :
$ x^3 - 6x^2 - 31x + 36 = 0 \rightarrow a = 1, b = -6, c = -31, d = 36 $.
dengan akar-akar : $ 9, x_1, \, $ dan $ x_2 $.
Operasi penjumlahan :
$\begin{align} 9 + x_1 + x_2 & = -\frac{b}{a} \\ 9 + x_1 + x_2 & = -\frac{(-6)}{1} \\ 9 + x_1 + x_2 & = 6 \\ x_1 + x_2 & = -3 \end{align}$
Operasi perkalian :
$\begin{align} 9 . x_1 . x_2 & = -\frac{d}{a} \\ 9 . x_1 . x_2 & = -\frac{36}{1} \\ 9 . x_1 . x_2 & = -36 \\ x_1 . x_2 & = -4 \end{align}$
Sehingga nilai :
$ x_1 + x_2 + x_1.x_2 = (-3) + (-4) = -7 $.
Jadi, nilai $ x_1 + x_2 + x_1.x_2 = -7 . \, \heartsuit $
$ x_1 + x_2 + x_3 = -\frac{b}{a} \, $ dan $ x_1 . x_2 . x_3 = -\frac{d}{a} $.
$\clubsuit \, $ Substitusi $x=9 $ ke persamaan
$\begin{align} x = 9 \rightarrow x^3 - 6x^2 - ax + b & = 0 \\ 9^3 - 6.9^2 - a.9 + b & = 0 \\ - 9a + b & = -243 \, \, \, \, \, \text{...pers(i)} \end{align}$
Sebelumnya diketahui : $ b - a = 5 \, $ ....pers(ii).
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} - 9a + b = -243 & \\ b - a = 5 & - \\ \hline -8a = - 248 & \\ a = 31 & \end{array}$
Pers(ii) : $ b - a = 5 \rightarrow b - 31 = 5 \rightarrow b = 36 $.
Persamaannya menjadi :
$ x^3 - 6x^2 - ax + b = 0 \rightarrow x^3 - 6x^2 - 31x + 36 = 0 $
$\clubsuit \, $ Operasi akar-akar persamaan :
Dari persamaan :
$ x^3 - 6x^2 - 31x + 36 = 0 \rightarrow a = 1, b = -6, c = -31, d = 36 $.
dengan akar-akar : $ 9, x_1, \, $ dan $ x_2 $.
Operasi penjumlahan :
$\begin{align} 9 + x_1 + x_2 & = -\frac{b}{a} \\ 9 + x_1 + x_2 & = -\frac{(-6)}{1} \\ 9 + x_1 + x_2 & = 6 \\ x_1 + x_2 & = -3 \end{align}$
Operasi perkalian :
$\begin{align} 9 . x_1 . x_2 & = -\frac{d}{a} \\ 9 . x_1 . x_2 & = -\frac{36}{1} \\ 9 . x_1 . x_2 & = -36 \\ x_1 . x_2 & = -4 \end{align}$
Sehingga nilai :
$ x_1 + x_2 + x_1.x_2 = (-3) + (-4) = -7 $.
Jadi, nilai $ x_1 + x_2 + x_1.x_2 = -7 . \, \heartsuit $
Nomor 8
Pertidaksamaan $ (3x)^{1 + {}^3 \log 3x } > 81x^2 \, $ mempunyai penyelesaian ....
$\spadesuit \, $ Konsep logaritma
*). Sifat : $ {}^a \log b^n = n {}^a \log b $
*). Definisi : $ {}^a \log b = c \leftrightarrow b = a^c $
*). Syarat logaritma : $ {}^a \log f(x) \rightarrow f(x) > 0 $.
$\spadesuit \, $ Menentukan syarat dari soalnya
bentuk : $ (3x)^{1 + {}^3 \log 3x } > 81x^2 \, $
Syaratnya pada $ {}^3 \log 3x \, $ adalah $ 3x > 0 \rightarrow x > 0 $.
Dari syarat $ x > 0 \, $ ini sebenarnya sudah bisa kita peroleh jawabannya yaitu opsi A karena opsi yang lainnya memuat negatif semua. Tetapi kita akan melanjutkan penyelesaiannya secara penuh.
Syarat ini kita anggap sebagai $ HP_1 = \{ x > 0 \} $
$\spadesuit \, $ Menyelesaikan soal :
Kedua ruas diberi $ {}^3 \log \, $ dan dimisalkan $ a = {}^3 \log x $,
$\begin{align} (3x)^{1 + {}^3 \log 3x } & > 81x^2 \\ {}^3 \log [(3x)^{1 + {}^3 \log 3x }] & > {}^3 \log [81x^2] \, \, \, \, \text{(dari sifat)} \\ (1 + {}^3 \log 3 + {}^3 \log x) ({}^3 \log 3 + {}^3 \log x) & > {}^3 \log 3^4 + 2 . {}^3 \log x \\ (1 + 1 + {}^3 \log x) (1 + {}^3 \log x) & > 4 + 2 . {}^3 \log x \\ (2 + a) (1 + a) & > 4 + 2 a \\ a^2 + 3a + 2 & > 4 + 2 a \\ a^2 + a - 2 & = 0 \\ (a - 1)(a+2) & = 0 \\ a = 1 \rightarrow {}^3 \log x & = 1 \rightarrow x = 3^1 = 3 \\ a = -2 \rightarrow {}^3 \log x & = -2 \rightarrow x = 3^{-2} = \frac{1}{9} \end{align}$

Karena yang diminta $ > 0 \, $ maka yang diarsir adalah yang positif,
sehingga $ HP_2 = \{ x < \frac{1}{9} \vee x > 3 \} $.
Solusi totalnya adalah :
$ HP = HP_1 \cap HP_2 = \{ x < \frac{1}{9} \vee x > 3 \} $.
Jadi, solusinya $ \{ x < \frac{1}{9} \vee x > 3 \} $, dan opsi yang sesuai adalah A. $\heartsuit $
*). Sifat : $ {}^a \log b^n = n {}^a \log b $
*). Definisi : $ {}^a \log b = c \leftrightarrow b = a^c $
*). Syarat logaritma : $ {}^a \log f(x) \rightarrow f(x) > 0 $.
$\spadesuit \, $ Menentukan syarat dari soalnya
bentuk : $ (3x)^{1 + {}^3 \log 3x } > 81x^2 \, $
Syaratnya pada $ {}^3 \log 3x \, $ adalah $ 3x > 0 \rightarrow x > 0 $.
Dari syarat $ x > 0 \, $ ini sebenarnya sudah bisa kita peroleh jawabannya yaitu opsi A karena opsi yang lainnya memuat negatif semua. Tetapi kita akan melanjutkan penyelesaiannya secara penuh.
Syarat ini kita anggap sebagai $ HP_1 = \{ x > 0 \} $
$\spadesuit \, $ Menyelesaikan soal :
Kedua ruas diberi $ {}^3 \log \, $ dan dimisalkan $ a = {}^3 \log x $,
$\begin{align} (3x)^{1 + {}^3 \log 3x } & > 81x^2 \\ {}^3 \log [(3x)^{1 + {}^3 \log 3x }] & > {}^3 \log [81x^2] \, \, \, \, \text{(dari sifat)} \\ (1 + {}^3 \log 3 + {}^3 \log x) ({}^3 \log 3 + {}^3 \log x) & > {}^3 \log 3^4 + 2 . {}^3 \log x \\ (1 + 1 + {}^3 \log x) (1 + {}^3 \log x) & > 4 + 2 . {}^3 \log x \\ (2 + a) (1 + a) & > 4 + 2 a \\ a^2 + 3a + 2 & > 4 + 2 a \\ a^2 + a - 2 & = 0 \\ (a - 1)(a+2) & = 0 \\ a = 1 \rightarrow {}^3 \log x & = 1 \rightarrow x = 3^1 = 3 \\ a = -2 \rightarrow {}^3 \log x & = -2 \rightarrow x = 3^{-2} = \frac{1}{9} \end{align}$

Karena yang diminta $ > 0 \, $ maka yang diarsir adalah yang positif,
sehingga $ HP_2 = \{ x < \frac{1}{9} \vee x > 3 \} $.
Solusi totalnya adalah :
$ HP = HP_1 \cap HP_2 = \{ x < \frac{1}{9} \vee x > 3 \} $.
Jadi, solusinya $ \{ x < \frac{1}{9} \vee x > 3 \} $, dan opsi yang sesuai adalah A. $\heartsuit $
Nomor 9
Tiga buah bilangan dengan jumlah 42 membentuk barisan geometri. Jika suku ditengah dikalikan dengan $ -\frac{5}{3} \, $
maka akan terbentuk barisan aritmetika. Maksimum dari bilangan-bilangan tersebut adalah ....
$\spadesuit \, $ Barisan geometri : $u_n=ar^{n-1} \, $
$\spadesuit \, $ Misalkan barisan geometrinya : $ a, ar, ar^2 $
$\begin{align} \text{jumlah } & = 42 \\ a + ar + ar^2 & = 42 \\ a(1 + r + r^2) & = 42 \\ a & = \frac{42}{1 + r + r^2} \, \, \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Suku tengah dikali $ - \frac{5}{3} \, $ , membentuk barisan aritmetika
barisannya : $ a, - \frac{5}{3}ar, ar^2 $
Barisan artimetika memiliki selisih sama , sehingga :
$\begin{align} u_2 - u_1 & = u_3 - u_2 \\ - \frac{5}{3}ar - a & = ar^2 - ( - \frac{5}{3}ar) \, \, \, \, \, \text{(kali 3)} \\ - 5ar - 3a & = 3ar^2 +5ar \, \, \, \, \, \text{(bagi } a) \\ - 5r - 3 & = 3r^2 +5r \\ 3r^2 + 10r + 3 & = 0 \\ (3r + 1)(r+3) & = 0 \\ r = -\frac{1}{3} \vee r & = -3 \\ \end{align}$
dari kedua rasio $(r) $ ini, sebenarnya barisannya sama saja, hanya dibalik saja barisannya. Sehingga cukup kita gunakan salah satu saja nilai rasionya yaitu $ r = -3 $.
$\spadesuit \, $ Menentukan nilai $ a \, $ dari pers(i) dan barisannya :
$ a = \frac{42}{1 + r + r^2} = \frac{42}{1 + (-3) + (-3)^2} = \frac{42}{7} = 6 $
kita peroleh nilai $ a = 6 \, $ dan $ r = -3 $.
barisannya : $ a, ar, ar^2 \rightarrow 6, \, -18, \, 54 $.
Jadi, nilai maksimum dari ketiga bilangannya adalah 54. $\heartsuit $
$\spadesuit \, $ Misalkan barisan geometrinya : $ a, ar, ar^2 $
$\begin{align} \text{jumlah } & = 42 \\ a + ar + ar^2 & = 42 \\ a(1 + r + r^2) & = 42 \\ a & = \frac{42}{1 + r + r^2} \, \, \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Suku tengah dikali $ - \frac{5}{3} \, $ , membentuk barisan aritmetika
barisannya : $ a, - \frac{5}{3}ar, ar^2 $
Barisan artimetika memiliki selisih sama , sehingga :
$\begin{align} u_2 - u_1 & = u_3 - u_2 \\ - \frac{5}{3}ar - a & = ar^2 - ( - \frac{5}{3}ar) \, \, \, \, \, \text{(kali 3)} \\ - 5ar - 3a & = 3ar^2 +5ar \, \, \, \, \, \text{(bagi } a) \\ - 5r - 3 & = 3r^2 +5r \\ 3r^2 + 10r + 3 & = 0 \\ (3r + 1)(r+3) & = 0 \\ r = -\frac{1}{3} \vee r & = -3 \\ \end{align}$
dari kedua rasio $(r) $ ini, sebenarnya barisannya sama saja, hanya dibalik saja barisannya. Sehingga cukup kita gunakan salah satu saja nilai rasionya yaitu $ r = -3 $.
$\spadesuit \, $ Menentukan nilai $ a \, $ dari pers(i) dan barisannya :
$ a = \frac{42}{1 + r + r^2} = \frac{42}{1 + (-3) + (-3)^2} = \frac{42}{7} = 6 $
kita peroleh nilai $ a = 6 \, $ dan $ r = -3 $.
barisannya : $ a, ar, ar^2 \rightarrow 6, \, -18, \, 54 $.
Jadi, nilai maksimum dari ketiga bilangannya adalah 54. $\heartsuit $
Nomor 10
Jika $ b,c \neq 0 \, $ dan $ \displaystyle \lim_{ x \to a } \frac{(x-a)\tan b(a-x)}{\cos c (x-a) \, - \, 1 } = d , \, $ maka $ b = .... $
$\clubsuit \, $ Konsep Dasar
*). Limit trogonometri :
$ \displaystyle \lim_{ x \to k } \frac{af(x)}{\sin bf(x)} = \frac{a}{b} \, $ dan $ \, \displaystyle \lim_{ x \to k } \frac{\tan af(x)}{\sin bf(x)} = \frac{a}{b} $
dengan syarat : $ f(k) = 0 $.
*). Bentuk : $ \cos pf(x) = 1 - 2\sin ^2 \frac{1}{2} p f(x) $.
$\clubsuit \, $ Modifikasi penyebutnya :
$\begin{align} \cos c(x-a) & = 1 - 2 \sin ^2 \frac{1}{2} c ( x- a) \\ \cos c(x-a) - 1 & = [1 - 2 \sin ^2 \frac{1}{2} c ( x- a) ] - 1 \\ & = - 2 \sin ^2 \frac{1}{2} c ( x- a) \\ & = - 2 \sin \frac{1}{2} c ( x- a) \sin \frac{1}{2} c ( x- a) \end{align}$
$\clubsuit \, $ Menyelesaikan soalnya
$\begin{align} \displaystyle \lim_{ x \to a } \frac{(x-a)\tan b(a-x)}{\cos c (x-a) \, - \, 1 } & = d \\ \displaystyle \lim_{ x \to a } \frac{(x-a)\tan -b(x-a)}{ - 2 \sin \frac{1}{2} c ( x- a) \sin \frac{1}{2} c ( x- a) } & = d \\ \frac{1}{-2} . \displaystyle \lim_{ x \to a } \frac{(x-a) }{ \sin \frac{1}{2} c ( x- a) } . \displaystyle \lim_{ x \to a } \frac{ \tan -b(x-a)}{ \sin \frac{1}{2} c ( x- a) }& = d \\ \frac{1}{-2} . \frac{ 1 }{ \frac{1}{2} c } . \frac{ -b }{ \frac{1}{2} c }& = d \\ \frac{b}{ \frac{1}{2} c^2 } & = d \\ b & = \frac{1}{2} c^2 d \end{align}$
Jadi, kita peroleh $ b = \frac{1}{2} c^2 d . \, \heartsuit $
*). Limit trogonometri :
$ \displaystyle \lim_{ x \to k } \frac{af(x)}{\sin bf(x)} = \frac{a}{b} \, $ dan $ \, \displaystyle \lim_{ x \to k } \frac{\tan af(x)}{\sin bf(x)} = \frac{a}{b} $
dengan syarat : $ f(k) = 0 $.
*). Bentuk : $ \cos pf(x) = 1 - 2\sin ^2 \frac{1}{2} p f(x) $.
$\clubsuit \, $ Modifikasi penyebutnya :
$\begin{align} \cos c(x-a) & = 1 - 2 \sin ^2 \frac{1}{2} c ( x- a) \\ \cos c(x-a) - 1 & = [1 - 2 \sin ^2 \frac{1}{2} c ( x- a) ] - 1 \\ & = - 2 \sin ^2 \frac{1}{2} c ( x- a) \\ & = - 2 \sin \frac{1}{2} c ( x- a) \sin \frac{1}{2} c ( x- a) \end{align}$
$\clubsuit \, $ Menyelesaikan soalnya
$\begin{align} \displaystyle \lim_{ x \to a } \frac{(x-a)\tan b(a-x)}{\cos c (x-a) \, - \, 1 } & = d \\ \displaystyle \lim_{ x \to a } \frac{(x-a)\tan -b(x-a)}{ - 2 \sin \frac{1}{2} c ( x- a) \sin \frac{1}{2} c ( x- a) } & = d \\ \frac{1}{-2} . \displaystyle \lim_{ x \to a } \frac{(x-a) }{ \sin \frac{1}{2} c ( x- a) } . \displaystyle \lim_{ x \to a } \frac{ \tan -b(x-a)}{ \sin \frac{1}{2} c ( x- a) }& = d \\ \frac{1}{-2} . \frac{ 1 }{ \frac{1}{2} c } . \frac{ -b }{ \frac{1}{2} c }& = d \\ \frac{b}{ \frac{1}{2} c^2 } & = d \\ b & = \frac{1}{2} c^2 d \end{align}$
Jadi, kita peroleh $ b = \frac{1}{2} c^2 d . \, \heartsuit $