Nomor 11
Jika jumlah kuadrat akar-akar real persamaan kuadrat $ x^2 - x - p = 0 \, $ sama dengan kuadrat jumlah kebalikan akar-akar
persamaan $ x^2-px-1 = 0, \, $ maka $ p = .... $
$\clubsuit \, $ PK1 : $ x^2 - x - p = 0 \, $ akar-akar $ x_1 \, $ dan $ x_2$
$\begin{align} x_1+x_2 & = \frac{-b}{a} = \frac{-(-1)}{1} = 1 \\ x_1x_2 & = \frac{c}{a} = \frac{-p}{1} = -p \\ x_1^2+x_2^2 & = (x_1+x_2)^2 - 2x_1x_2 \\ & = (1)^2 - 2(-p) = 1 + 2p \end{align}$
$\clubsuit \, $ PK2 : $ x^2-px-1 = 0, \, $ akar-akar $ y_1 \, $ dan $ y_2$
$\begin{align} y_1+y_2 & = \frac{-b}{a} = \frac{-(-p)}{1} = p \\ y_1y_2 & = \frac{c}{a} = \frac{-1}{1} = -1 \\ \frac{1}{y_1} + \frac{1}{y_2} & = \frac{y_1+y_2}{y_1y_2} = \frac{p}{-1} = -p \end{align}$
$\clubsuit \, $ Jumlah kuadrat PK1 = kuadrat jumlah kebalikan PK2
$\begin{align} x_1^2+x_2^2 & = (\frac{1}{y_1} + \frac{1}{y_2})^2 \\ 1 + 2p & = (-p)^2 \\ p^2 - 2p - 1 & = 0 \\ p & = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \, \, \text{(rumus ABC)} \\ p & = \frac{2 \pm \sqrt{(-2)^2-4.1.(-1)}}{2.1} \\ p & = \frac{2 \pm \sqrt{8}}{2} \\ p & = \frac{2 \pm 2\sqrt{2}}{2} \\ p & = 1 \pm \sqrt{2} \end{align}$
Jadi, nilai $ p = \sqrt{2} + 1 \vee p = -\sqrt{2} + 1 . \heartsuit $
$\begin{align} x_1+x_2 & = \frac{-b}{a} = \frac{-(-1)}{1} = 1 \\ x_1x_2 & = \frac{c}{a} = \frac{-p}{1} = -p \\ x_1^2+x_2^2 & = (x_1+x_2)^2 - 2x_1x_2 \\ & = (1)^2 - 2(-p) = 1 + 2p \end{align}$
$\clubsuit \, $ PK2 : $ x^2-px-1 = 0, \, $ akar-akar $ y_1 \, $ dan $ y_2$
$\begin{align} y_1+y_2 & = \frac{-b}{a} = \frac{-(-p)}{1} = p \\ y_1y_2 & = \frac{c}{a} = \frac{-1}{1} = -1 \\ \frac{1}{y_1} + \frac{1}{y_2} & = \frac{y_1+y_2}{y_1y_2} = \frac{p}{-1} = -p \end{align}$
$\clubsuit \, $ Jumlah kuadrat PK1 = kuadrat jumlah kebalikan PK2
$\begin{align} x_1^2+x_2^2 & = (\frac{1}{y_1} + \frac{1}{y_2})^2 \\ 1 + 2p & = (-p)^2 \\ p^2 - 2p - 1 & = 0 \\ p & = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \, \, \text{(rumus ABC)} \\ p & = \frac{2 \pm \sqrt{(-2)^2-4.1.(-1)}}{2.1} \\ p & = \frac{2 \pm \sqrt{8}}{2} \\ p & = \frac{2 \pm 2\sqrt{2}}{2} \\ p & = 1 \pm \sqrt{2} \end{align}$
Jadi, nilai $ p = \sqrt{2} + 1 \vee p = -\sqrt{2} + 1 . \heartsuit $
Nomor 12
Nilai-nilai $ x \, $ yang memenuhi pertaksamaan $ |x-2| \geq \sqrt{2x+20} \, $ adalah ....
$\spadesuit \, $ Konsep dasar : $ |x|^2 = x^2 $
$\spadesuit \, $ Syarat dalam akar positif
$ \sqrt{2x+20} \geq 0 \rightarrow 2x + 20 \geq 0 \rightarrow x \geq -10 \, \, $ ...(HP1)
$\spadesuit \, $ Kuadratkan pertidaksamaan
$\begin{align} (|x-2|)^2 & \geq ( \sqrt{2x+20} )^2 \\ (x-2)^2 & \geq 2x + 20 \\ x^2 - 4x + 4 & \geq 2x + 20 \\ x^2 - 6x - 16 & \geq 0 \\ (x+2)(x-8) & = 0 \\ x = -2 & \vee x = 8 \end{align}$
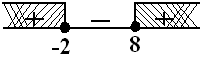
$ HP2 = \{ x \leq -2 \vee x \geq 8 \} $
Sehingga solusinya :
$\begin{align} HP & = HP1 \cap HP2 \\ HP & = \{ -10 \leq x \leq -2 \vee x \geq 8 \} \, \, \text{(atau)} \\ HP & = \{ -10 \leq x \leq -2 \vee 8 \leq x < \infty \} \end{align}$
Jadi, solusinya $ HP = \{ -10 \leq x \leq -2 \vee 8 \leq x < \infty \} . \heartsuit $
$\spadesuit \, $ Syarat dalam akar positif
$ \sqrt{2x+20} \geq 0 \rightarrow 2x + 20 \geq 0 \rightarrow x \geq -10 \, \, $ ...(HP1)
$\spadesuit \, $ Kuadratkan pertidaksamaan
$\begin{align} (|x-2|)^2 & \geq ( \sqrt{2x+20} )^2 \\ (x-2)^2 & \geq 2x + 20 \\ x^2 - 4x + 4 & \geq 2x + 20 \\ x^2 - 6x - 16 & \geq 0 \\ (x+2)(x-8) & = 0 \\ x = -2 & \vee x = 8 \end{align}$
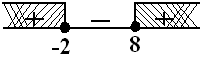
$ HP2 = \{ x \leq -2 \vee x \geq 8 \} $
Sehingga solusinya :
$\begin{align} HP & = HP1 \cap HP2 \\ HP & = \{ -10 \leq x \leq -2 \vee x \geq 8 \} \, \, \text{(atau)} \\ HP & = \{ -10 \leq x \leq -2 \vee 8 \leq x < \infty \} \end{align}$
Jadi, solusinya $ HP = \{ -10 \leq x \leq -2 \vee 8 \leq x < \infty \} . \heartsuit $
Nomor 13
Diberikan ABCD.EFGH. Perbandingan luas permukaan kubus ABCD.EFGH dengan limas H.ACF adalah ....
$\spadesuit \, $ Misalkan panjang rusuknya 2

$\spadesuit \, $ Menentukan luas permukaan kubus
$L_{kb} = 6.s^2 = 6.2^2 = 24 $
$\spadesuit \, $ Sisi limas H.ACF memiliki luas yang sama
$\Delta HDM, \, HM = \sqrt{HD^2+DM^2} = \sqrt{2^2+(\sqrt{2})^2} = \sqrt{6} $
$L_{ACH} = \frac{1}{2}.AC.HM = \frac{1}{2}. 2\sqrt{2}.\sqrt{6} = 2\sqrt{3} $
$\spadesuit \, $ Menentukan luas permukaan limas H.ACF
$L_{H.ACF} = 4. L_{ACH} = 4. 2\sqrt{3} = 8\sqrt{3} $
Sehingga perbandingannya :
$\begin{align} \frac{L_{kb}}{L_{H.ACF}} & = \frac{24}{8\sqrt{3}} = \frac{3}{\sqrt{3}} = \frac{\sqrt{3}}{1} \end{align}$
Jadi, perbandingan luas kubus dan limas adalah $ \sqrt{3} : 1 . \heartsuit $

$\spadesuit \, $ Menentukan luas permukaan kubus
$L_{kb} = 6.s^2 = 6.2^2 = 24 $
$\spadesuit \, $ Sisi limas H.ACF memiliki luas yang sama
$\Delta HDM, \, HM = \sqrt{HD^2+DM^2} = \sqrt{2^2+(\sqrt{2})^2} = \sqrt{6} $
$L_{ACH} = \frac{1}{2}.AC.HM = \frac{1}{2}. 2\sqrt{2}.\sqrt{6} = 2\sqrt{3} $
$\spadesuit \, $ Menentukan luas permukaan limas H.ACF
$L_{H.ACF} = 4. L_{ACH} = 4. 2\sqrt{3} = 8\sqrt{3} $
Sehingga perbandingannya :
$\begin{align} \frac{L_{kb}}{L_{H.ACF}} & = \frac{24}{8\sqrt{3}} = \frac{3}{\sqrt{3}} = \frac{\sqrt{3}}{1} \end{align}$
Jadi, perbandingan luas kubus dan limas adalah $ \sqrt{3} : 1 . \heartsuit $
Nomor 14
Jika suku banyak $ 2x^3-px^2+qx+6 \, $ dan $ \, 2x^3+3x^2-4x-1 , \, $ mempunyai sisa sama apabila dibagi oleh $ x+1, \, $
maka nilai $ p+q = .... $
$\spadesuit \, $ Teorema sisa : $ \frac{P(x)}{x+a} \rightarrow \, \text{sisa} \, = P(-a) $
$\spadesuit \, $ Misalkan :
$ f(x) = 2x^3-px^2+qx+6 \, $ dan $ \, g(x) = 2x^3+3x^2-4x-1 $
$\spadesuit \, $ Menentukan sisa setiap pembagian
$ \frac{f(x)}{x+1} \rightarrow \, \text{sisa I} \, = f(-1) $
$ \frac{g(x)}{x+1} \rightarrow \, \text{sisa II} \, = g(-1) $
$\spadesuit \, $ Sisa pembagian sama :
$\begin{align} \text{sisa I} & = \text{sisa II} \\ f(-1) & = g(-1) \\ 2.(-1)^3-p.(-1)^2+q.(-1)+6 & = 2.(-1)^3+3.(-1)^2-4.(-1)-1 \\ -2-p-q+6 & = -2 + 3 + 4 - 1 \\ p+q & = 0 \end{align}$
Jadi, nilai $ p+q = 0. \heartsuit $
$\spadesuit \, $ Misalkan :
$ f(x) = 2x^3-px^2+qx+6 \, $ dan $ \, g(x) = 2x^3+3x^2-4x-1 $
$\spadesuit \, $ Menentukan sisa setiap pembagian
$ \frac{f(x)}{x+1} \rightarrow \, \text{sisa I} \, = f(-1) $
$ \frac{g(x)}{x+1} \rightarrow \, \text{sisa II} \, = g(-1) $
$\spadesuit \, $ Sisa pembagian sama :
$\begin{align} \text{sisa I} & = \text{sisa II} \\ f(-1) & = g(-1) \\ 2.(-1)^3-p.(-1)^2+q.(-1)+6 & = 2.(-1)^3+3.(-1)^2-4.(-1)-1 \\ -2-p-q+6 & = -2 + 3 + 4 - 1 \\ p+q & = 0 \end{align}$
Jadi, nilai $ p+q = 0. \heartsuit $
Nomor 15
Tiga bilangan merupakan suku-suku deret aritmatika. Jika suku pertama dikurangi 2 dan suku ketiga ditambah 6, maka barisan menjadi
barisan geometri dengan rasio 2. Hasil kali ketiga bilangan pada barisan geometri tersebut adalah ....
$\clubsuit \, $ Misalkan barisannya : $ x, y, z $
Barisan aritmatika, selisih sama
$ y-x = z-y \rightarrow x + z = 2y \, \, $ ...pers(i)
$\clubsuit \, $ Perubahan barisan
Barisan geometri : $ x-2,y,z+6 $
Rasio sama : $ r = \frac{y}{x-2} = \frac{z+6}{y} \leftrightarrow 2 = \frac{y}{x-2} = \frac{z+6}{y} $
Bentuk persamaan dari persamaan pada barisan geometri
$ \frac{y}{x-2} = 2 \rightarrow y = 2x-4 \, \, $ ...pers(ii)
$ \frac{z+6}{y} = 2 \rightarrow z+6 = 2y \, \, $ ...pers(iii)
$\clubsuit \, $ Eliminasi pers(i) dan pers(iii)
$\begin{array}{cc} x + z = 2y & \\ z+6 = 2y & - \\ \hline x = 6 & \end{array}$
pers(ii): $ y = 2x-4 \rightarrow y = 2.6-4 = 12-4 = 8 $
pers(iii): $ z+6 = 2y \rightarrow z+6 = 2.8 \rightarrow z = 10 $
Sehingga barisan geometrinya menjadi :
$ x-2,y,z+6 \rightarrow 6-2,8,10+6 \rightarrow 4, 8, 16$
Hasil perkaliannya : 4$\times$8$\times$16 = 512
Jadi, hasil perkalian barisan geometrinya adalah 512. $ \heartsuit $
Barisan aritmatika, selisih sama
$ y-x = z-y \rightarrow x + z = 2y \, \, $ ...pers(i)
$\clubsuit \, $ Perubahan barisan
Barisan geometri : $ x-2,y,z+6 $
Rasio sama : $ r = \frac{y}{x-2} = \frac{z+6}{y} \leftrightarrow 2 = \frac{y}{x-2} = \frac{z+6}{y} $
Bentuk persamaan dari persamaan pada barisan geometri
$ \frac{y}{x-2} = 2 \rightarrow y = 2x-4 \, \, $ ...pers(ii)
$ \frac{z+6}{y} = 2 \rightarrow z+6 = 2y \, \, $ ...pers(iii)
$\clubsuit \, $ Eliminasi pers(i) dan pers(iii)
$\begin{array}{cc} x + z = 2y & \\ z+6 = 2y & - \\ \hline x = 6 & \end{array}$
pers(ii): $ y = 2x-4 \rightarrow y = 2.6-4 = 12-4 = 8 $
pers(iii): $ z+6 = 2y \rightarrow z+6 = 2.8 \rightarrow z = 10 $
Sehingga barisan geometrinya menjadi :
$ x-2,y,z+6 \rightarrow 6-2,8,10+6 \rightarrow 4, 8, 16$
Hasil perkaliannya : 4$\times$8$\times$16 = 512
Jadi, hasil perkalian barisan geometrinya adalah 512. $ \heartsuit $