Nomor 6
Jika $ x + 2y = 2a + 1 \, $ dan $ 3x-y = a + p , \, $ maka $ 5x - 4y = .... $
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{c|c|cc} x + 2y = 2a + 1 & \times 1 & x + 2y = 2a + 1 & \\ 3x-y = a + p & \times 2 & 6x - 2y = 2a + 2p & + \\ \hline & & 7x = 4a + 2p + 1 & \\ & & x = \frac{1}{7} (4a + 2p + 1) & \end{array} $
$\begin{align} \text{pers(i) : } \, x + 2y & = 2a + 1 \\ \frac{1}{7} (4a + 2p + 1) + 2y & = 2a + 1 \\ y & = \frac{1}{7}(5a-p+3) \end{align}$
Sehingga nilai $ 5x - 4y = 5. \frac{1}{7} (4a + 2p + 1) - 4.\frac{1}{7}(5a-p+3) = 2p - 1 $
Jadi, nilai $ 5x - 4y = 2p -1 . \heartsuit $
$\begin{array}{c|c|cc} x + 2y = 2a + 1 & \times 1 & x + 2y = 2a + 1 & \\ 3x-y = a + p & \times 2 & 6x - 2y = 2a + 2p & + \\ \hline & & 7x = 4a + 2p + 1 & \\ & & x = \frac{1}{7} (4a + 2p + 1) & \end{array} $
$\begin{align} \text{pers(i) : } \, x + 2y & = 2a + 1 \\ \frac{1}{7} (4a + 2p + 1) + 2y & = 2a + 1 \\ y & = \frac{1}{7}(5a-p+3) \end{align}$
Sehingga nilai $ 5x - 4y = 5. \frac{1}{7} (4a + 2p + 1) - 4.\frac{1}{7}(5a-p+3) = 2p - 1 $
Jadi, nilai $ 5x - 4y = 2p -1 . \heartsuit $
Cara II :
$\spadesuit \, $ Tanpa menentukan nilai $ x \, $ dan $ y , \, $ tetapi langsung mengarahkan yang ditanyakan
$\begin{array}{c|c|cc} x + 2y = 2a + 1 & \times 1 & x + 2y = 2a + 1 & \\ 3x-y = a + p & \times 2 & 6x - 2y = 2a + 2p & - \\ \hline & & -5x + 4y = 1 - 2p & \end{array} $
Kali -1 bentuk $ -5x + 4y = 1 - 2p , \, $ diperoleh $ 5x - 4y = 2p -1 \, $ dan hasil ini sama dengan yang ditanyakan.
Jadi, nilai $ 5x - 4y = 2p -1 . \heartsuit $
Catatan : Metode ini digunakan hanya untuk kasus tertentu yang artinya tidak semua sistem persamaan bisa dikerjakan dengan metode ini. Operasi yang dilakukan bisa jumlah, pengurangan, atau dikalikan dengan bilangan tertentu terlebih dulu sehingga ketika semua persamaan yang ada dioperasikan akan diperoleh langsung hasil yang ditanyakan seperti soal di atas.
$\spadesuit \, $ Tanpa menentukan nilai $ x \, $ dan $ y , \, $ tetapi langsung mengarahkan yang ditanyakan
$\begin{array}{c|c|cc} x + 2y = 2a + 1 & \times 1 & x + 2y = 2a + 1 & \\ 3x-y = a + p & \times 2 & 6x - 2y = 2a + 2p & - \\ \hline & & -5x + 4y = 1 - 2p & \end{array} $
Kali -1 bentuk $ -5x + 4y = 1 - 2p , \, $ diperoleh $ 5x - 4y = 2p -1 \, $ dan hasil ini sama dengan yang ditanyakan.
Jadi, nilai $ 5x - 4y = 2p -1 . \heartsuit $
Catatan : Metode ini digunakan hanya untuk kasus tertentu yang artinya tidak semua sistem persamaan bisa dikerjakan dengan metode ini. Operasi yang dilakukan bisa jumlah, pengurangan, atau dikalikan dengan bilangan tertentu terlebih dulu sehingga ketika semua persamaan yang ada dioperasikan akan diperoleh langsung hasil yang ditanyakan seperti soal di atas.
Nomor 7
Penyelesaian pertidaksamaan $ \left( \frac{x-1}{x} \right)^2 \leq 4\left( 1 - \frac{1}{x} \right) - 3 \, $ adalah ....
$\clubsuit \, $ Menentukan akar-akar pembilang dan penyebutnya
$\begin{align} \left( \frac{x-1}{x} \right)^2 & \leq 4\left( 1 - \frac{1}{x} \right) - 3 \\ \frac{x^2-2x+1}{x^2} & \leq 4 - \frac{4}{x} - 3 \\ \frac{x^2-2x+1}{x^2} & \leq 1 - \frac{4}{x} \\ \frac{x^2-2x+1}{x^2} + \frac{4}{x} - 1 & \leq 0 \\ \frac{x^2-2x+1}{x^2} + \frac{4x}{x^2} - \frac{x^2}{x^2} & \leq 0 \\ \frac{x^2-2x+1 + 4x - x^2}{x^2} & \leq 0 \\ \frac{2x+1}{x^2} & \leq 0 \\ x = - \frac{1}{2} \vee x & = 0 \end{align} $
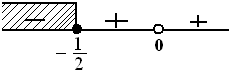
Jadi, solusinya $ HP = \{ x \leq - \frac{1}{2} \} . \heartsuit$
$\begin{align} \left( \frac{x-1}{x} \right)^2 & \leq 4\left( 1 - \frac{1}{x} \right) - 3 \\ \frac{x^2-2x+1}{x^2} & \leq 4 - \frac{4}{x} - 3 \\ \frac{x^2-2x+1}{x^2} & \leq 1 - \frac{4}{x} \\ \frac{x^2-2x+1}{x^2} + \frac{4}{x} - 1 & \leq 0 \\ \frac{x^2-2x+1}{x^2} + \frac{4x}{x^2} - \frac{x^2}{x^2} & \leq 0 \\ \frac{x^2-2x+1 + 4x - x^2}{x^2} & \leq 0 \\ \frac{2x+1}{x^2} & \leq 0 \\ x = - \frac{1}{2} \vee x & = 0 \end{align} $
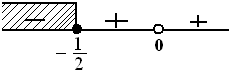
Jadi, solusinya $ HP = \{ x \leq - \frac{1}{2} \} . \heartsuit$
Nomor 8
Jika $ \cos x=2\sin x $ , maka nilai $ \sin x \cos x $ adalah ...
$\spadesuit \, $ Menentukan nilai $ \tan x$ dengan $\tan x=\frac{\sin x}{\cos x}$ :
$\cos x=2\sin x \Leftrightarrow \frac{\sin x}{\cos x}=\frac{1}{2} \Leftrightarrow \tan x=\frac{1}{2}$
$\spadesuit \, $ Buat segitiga dari nilai $\tan x=\frac{1}{2}$ :
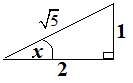
sehingga $\sin x\cos x=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jadi, nilai $ \sin x\cos x=\frac{2}{5}. \, \heartsuit $
$\cos x=2\sin x \Leftrightarrow \frac{\sin x}{\cos x}=\frac{1}{2} \Leftrightarrow \tan x=\frac{1}{2}$
$\spadesuit \, $ Buat segitiga dari nilai $\tan x=\frac{1}{2}$ :

sehingga $\sin x\cos x=\frac{1}{\sqrt{5}}.\frac{2}{\sqrt{5}}=\frac{2}{5}$
Jadi, nilai $ \sin x\cos x=\frac{2}{5}. \, \heartsuit $
Nomor 9
Jika $ a_1, \, a_2, \, a_3 \, $ adalah barisan aritmetika dan $ a_1, \, a_2, \, a_1 + a_3 \, $ adalah barisan geometri,
maka $ \frac{a_3}{a_1} = .... $
$\clubsuit \, $ Barisan aritmetika : $ a_1, \, a_2, \, a_3 \, $
Selisih sama : $ a_2 - a_1 = a_3 - a_2 \rightarrow a_1 + a_3 = 2a_2 \, $ ...pers(i)
$\clubsuit \, $ Barisan geometri : $ a_1, \, a_2, \, a_1 + a_3 \, $
Dari pers(i), maka barisan geometrinya menjadi : $ a_1, \, a_2, \, 2a_2 $
Rasio sama : $ \frac{a_2}{a_1} = \frac{2a_2}{a_2} \rightarrow \frac{a_2}{a_1} = 2 \rightarrow a_2 = 2a_1 $
$\clubsuit \, $ Menentukan nilai $ \frac{a_3}{a_1} \, $ dengan $ a_2 = 2a_1 $
$\begin{align} \text{pers(i) : } \, a_1 + a_3 & = 2a_2 \\ a_1 + a_3 & = 2.(2a_1) \\ a_1 + a_3 & = 4a_1 \\ a_3 & = 3a_1 \\ \frac{a_3}{a_1} & = 3 \end{align}$
Jadi, nilai $ \frac{a_3}{a_1} = 3 . \heartsuit $
Selisih sama : $ a_2 - a_1 = a_3 - a_2 \rightarrow a_1 + a_3 = 2a_2 \, $ ...pers(i)
$\clubsuit \, $ Barisan geometri : $ a_1, \, a_2, \, a_1 + a_3 \, $
Dari pers(i), maka barisan geometrinya menjadi : $ a_1, \, a_2, \, 2a_2 $
Rasio sama : $ \frac{a_2}{a_1} = \frac{2a_2}{a_2} \rightarrow \frac{a_2}{a_1} = 2 \rightarrow a_2 = 2a_1 $
$\clubsuit \, $ Menentukan nilai $ \frac{a_3}{a_1} \, $ dengan $ a_2 = 2a_1 $
$\begin{align} \text{pers(i) : } \, a_1 + a_3 & = 2a_2 \\ a_1 + a_3 & = 2.(2a_1) \\ a_1 + a_3 & = 4a_1 \\ a_3 & = 3a_1 \\ \frac{a_3}{a_1} & = 3 \end{align}$
Jadi, nilai $ \frac{a_3}{a_1} = 3 . \heartsuit $
Nomor 10
Jika $ A = \left( \begin{matrix} -1 & -1 & 0 \\ -1 & 1 & 2 \end{matrix} \right), \, B = \left( \begin{matrix} -1 & x \\ 1 & y \\ 0 & z \end{matrix} \right), \, $
dan $ AB = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) , \, $ maka nilai $ z - x \, $ adalah ....
$\spadesuit \, $ Menentukan hasil kali matriksnya
$\begin{align} AB & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \\ \left( \begin{matrix} -1 & -1 & 0 \\ -1 & 1 & 2 \end{matrix} \right). \left( \begin{matrix} -1 & x \\ 1 & y \\ 0 & z \end{matrix} \right) & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \\ \left( \begin{matrix} 0 & -x-y \\ 2 & -x+y+2z \end{matrix} \right) & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \end{align}$
Diperoleh persamaan :
$ -x-y = 2 \, $ ...pers(i) dan $ -x+y+2z = 4 \, $ ....pers(ii)
$\spadesuit \, $ Jumlahkan kedua persamaan
$\begin{array}{cc} -x-y = 2 & \\ -x+y+2z = 4 & + \\ \hline -2x + 2z = 6 & \\ -x + z = 3 & \end{array} $
Sehingga nilai $ z - x = -x + z = 3 $
Jadi, nilai $ z - x = 3 . \heartsuit $
$\begin{align} AB & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \\ \left( \begin{matrix} -1 & -1 & 0 \\ -1 & 1 & 2 \end{matrix} \right). \left( \begin{matrix} -1 & x \\ 1 & y \\ 0 & z \end{matrix} \right) & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \\ \left( \begin{matrix} 0 & -x-y \\ 2 & -x+y+2z \end{matrix} \right) & = \left( \begin{matrix} 0 & 2 \\ 2 & 4 \end{matrix} \right) \end{align}$
Diperoleh persamaan :
$ -x-y = 2 \, $ ...pers(i) dan $ -x+y+2z = 4 \, $ ....pers(ii)
$\spadesuit \, $ Jumlahkan kedua persamaan
$\begin{array}{cc} -x-y = 2 & \\ -x+y+2z = 4 & + \\ \hline -2x + 2z = 6 & \\ -x + z = 3 & \end{array} $
Sehingga nilai $ z - x = -x + z = 3 $
Jadi, nilai $ z - x = 3 . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.