Nomor 11
Jika $A=\left( \begin{matrix} a & b & c \\ -1 & 1 & 2 \end{matrix} \right) , \, B=\left( \begin{matrix} 2 & 2 \\ -1 & 1 \\ 4 & 0 \end{matrix} \right)$ ,
dan $ AB = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right), \, $ maka nilai $ a + c \, $ adalah ...
$\spadesuit \, $ Menentukan perkaliannya
$\begin{align} AB & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \left( \begin{matrix} a & b & c \\ -1 & 1 & 2 \end{matrix} \right)\left( \begin{matrix} 2 & 2 \\ -1 & 1 \\ 4 & 0 \end{matrix} \right) & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \left( \begin{matrix} 2a-b+4c & 2a+b \\ 5 & -1 \end{matrix} \right) & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \text{diperoleh persamaan} & \\ 2a-b+4c & = 3 \, \, \, \, \text{....pers(i)} \\ 2a+b & = 1 \, \, \, \, \text{....pers(ii)} \end{align} $
$\spadesuit \, $ Jumlahkan kedua persamaan
$\begin{array}{cc} 2a-b+4c = 3 & \\ 2a+b = 1 & + \\ \hline 4a+4c = 4 & \\ a+c = 1 & \end{array} $
Jadi, nilai $ a + c = 1 . \heartsuit $
$\begin{align} AB & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \left( \begin{matrix} a & b & c \\ -1 & 1 & 2 \end{matrix} \right)\left( \begin{matrix} 2 & 2 \\ -1 & 1 \\ 4 & 0 \end{matrix} \right) & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \left( \begin{matrix} 2a-b+4c & 2a+b \\ 5 & -1 \end{matrix} \right) & = \left( \begin{matrix} 3 & 1 \\ 5 & -1 \end{matrix} \right) \\ \text{diperoleh persamaan} & \\ 2a-b+4c & = 3 \, \, \, \, \text{....pers(i)} \\ 2a+b & = 1 \, \, \, \, \text{....pers(ii)} \end{align} $
$\spadesuit \, $ Jumlahkan kedua persamaan
$\begin{array}{cc} 2a-b+4c = 3 & \\ 2a+b = 1 & + \\ \hline 4a+4c = 4 & \\ a+c = 1 & \end{array} $
Jadi, nilai $ a + c = 1 . \heartsuit $
Nomor 12
Diketahui $a, \, b,$ dan $c$ berturut-turut adalah suku ke-2, ke-4, dan ke-6 suatu barisan aritmetika. Jika $ \frac{a+b+c}{b+1}=4, \, $
maka nilai $ b \, $ adalah .....
$\clubsuit \, u_2=a, \, u_4=b, \, $ dan $u_6=c \, $ barisan aritmatika .
Suatu barisan aritmetika yang berurutan (contoh : $ u_1, u_2, u_3 \, $ atau $ u_3,u_4,u_5 \, $ atau $ u_1,u_3,u_5 \, $ atau $ u_2,u_4,u_6 $) pasti mempunyai selisih yang sama.
*). selisih sama : $b-a = c - b \Rightarrow a+c = 2b \, $ ...pers(i)
*). dari soal diketahui juga : $\frac{a+b+c}{b+1}=4 \, $ ...per(ii)
$\clubsuit \, $ Substiutusi pers(i) ke pers(ii)
$\begin{align} \frac{a+b+c}{b+1} & =4 \\ \frac{(a+c)+b}{b+1} & =4 \, \, \, \, \text{(posisi b dan c ditukar)} \\ \frac{(2b)+b}{b+1} & =4 \\ \frac{3b}{b+1} & =4 \\ 3b & = 4b + 4 \\ b & = -4 \end{align}$
Sehingga nilai $ b = -4 $
Jadi, nilai $b=-4. \heartsuit $
Suatu barisan aritmetika yang berurutan (contoh : $ u_1, u_2, u_3 \, $ atau $ u_3,u_4,u_5 \, $ atau $ u_1,u_3,u_5 \, $ atau $ u_2,u_4,u_6 $) pasti mempunyai selisih yang sama.
*). selisih sama : $b-a = c - b \Rightarrow a+c = 2b \, $ ...pers(i)
*). dari soal diketahui juga : $\frac{a+b+c}{b+1}=4 \, $ ...per(ii)
$\clubsuit \, $ Substiutusi pers(i) ke pers(ii)
$\begin{align} \frac{a+b+c}{b+1} & =4 \\ \frac{(a+c)+b}{b+1} & =4 \, \, \, \, \text{(posisi b dan c ditukar)} \\ \frac{(2b)+b}{b+1} & =4 \\ \frac{3b}{b+1} & =4 \\ 3b & = 4b + 4 \\ b & = -4 \end{align}$
Sehingga nilai $ b = -4 $
Jadi, nilai $b=-4. \heartsuit $
Nomor 13
Diketahui deret geometri tak hingga $u_1+u_2+u_3+...$ . Jika rasio deret tersebut adalah $r$ dengan $ -1 < r < 1 $ ,
$u_2+u_4+u_6...=4$ , dan $u_2+u_4= \frac{15}{4} $ , maka nilai $r$ adalah ...
$\spadesuit \, $ Rumus dasar :
Jumlah geometri tak hingga genap : $S_{\infty} (\text{genap}) = \frac{ar}{1-r^2} $
Suku ke-n : $U_n=ar^{n-1}$
$\spadesuit \, $ Menyederhanakan bentuk $u_2+u_4+u_6...=4$
$\begin{align} u_2+u_4+u_6... & = 4 \\ S_{\infty} (\text{genap}) & = 4 \\ \frac{ar}{1-r^2} & = 4 \\ ar & = 4 (1-r^2) \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Menyederhanakan bentuk $u_2+u_4=\frac{15}{4}$
$\begin{align} u_2+u_4 & = \frac{15}{4} \\ ar + ar^3 & = \frac{15}{4} \\ ar(1+r^2) & = \frac{15}{4} \\ ar & = \frac{15}{4(1+r^2)} \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers(ii) ke pers(i) :
$\begin{align} ar & = 4 (1-r^2) \, \, \text{...pers(i)} \\ \frac{15}{4(1+r^2)} & = 4 (1-r^2) \, \, \text{(kali silang)}\\ 15 & = 16 (1-r^2)(1+r^2) \\ 15 & = 16 \left[ 1-(r^2)^2 \right] \\ \frac{15}{16} & = 1 - (r^2)^2 \\ (r^2)^2 & = 1- \frac{15}{16} \\ (r^2)^2 & = \frac{1}{16} \\ (r^2) & = \frac{1}{4} \\ r & = \pm \sqrt{\frac{1}{4}} \Leftrightarrow r = \pm \frac{1}{2} \end{align}$
Jadi, nilai $ r = \pm \frac{1}{2} . \heartsuit $
Jumlah geometri tak hingga genap : $S_{\infty} (\text{genap}) = \frac{ar}{1-r^2} $
Suku ke-n : $U_n=ar^{n-1}$
$\spadesuit \, $ Menyederhanakan bentuk $u_2+u_4+u_6...=4$
$\begin{align} u_2+u_4+u_6... & = 4 \\ S_{\infty} (\text{genap}) & = 4 \\ \frac{ar}{1-r^2} & = 4 \\ ar & = 4 (1-r^2) \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Menyederhanakan bentuk $u_2+u_4=\frac{15}{4}$
$\begin{align} u_2+u_4 & = \frac{15}{4} \\ ar + ar^3 & = \frac{15}{4} \\ ar(1+r^2) & = \frac{15}{4} \\ ar & = \frac{15}{4(1+r^2)} \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers(ii) ke pers(i) :
$\begin{align} ar & = 4 (1-r^2) \, \, \text{...pers(i)} \\ \frac{15}{4(1+r^2)} & = 4 (1-r^2) \, \, \text{(kali silang)}\\ 15 & = 16 (1-r^2)(1+r^2) \\ 15 & = 16 \left[ 1-(r^2)^2 \right] \\ \frac{15}{16} & = 1 - (r^2)^2 \\ (r^2)^2 & = 1- \frac{15}{16} \\ (r^2)^2 & = \frac{1}{16} \\ (r^2) & = \frac{1}{4} \\ r & = \pm \sqrt{\frac{1}{4}} \Leftrightarrow r = \pm \frac{1}{2} \end{align}$
Jadi, nilai $ r = \pm \frac{1}{2} . \heartsuit $
Nomor 14
Parabola $y=x^2-(k+2)x+2k $ memotong sumbu-Y di (0,$c$) dan memotong sumbu-X di ($a$,0) dan ($b$,0). Jika $a+2, \, c, \, $ dan $ a + 2b \, $
membentuk barisan aritmetika, maka nilai $ k \,$ adalah ...
$\clubsuit \,$ Substitusi titik (0,c) ke parabola : $y=x^2-(k+2)x+2k $
$y=x^2-(k+2)x+2k \Rightarrow c=0^2-(k+2).0+2k $
$ \Rightarrow c = 2k. $
$\clubsuit \, $ Parabola memotong sumbu X di (a,0) dan (b,0) , artinya a dan b adalah akar-akar dari $ x^2-(k+2)x+2k = 0 \, $ , sehingga berlaku rumus penjumlahan akar-akar :
$a+b = \frac{-b}{a} = \frac{-(-(k+2))}{1} \Leftrightarrow a+b = k + 2 \, $ ...pers(i)
$\clubsuit \,$ Barisan aritmatika $a+2, \, c, \, $ dan $ a + 2b \, $ , selisihnya sama :
$\begin{align} (c) - (a+2) & = (a+2b) - (c) \\ 2c & = (a+2b) + (a+2) \\ 2c & = 2(a+b) + 2 \\ \text{(gunakan pers(i) dan } & \, c = 2k )\\ 2.(2k) & = 2(k+2) + 2 \\ 4k & = 2k + 6 \\ 2k & = 6 \\ k & = \frac{6}{2} = 3 \end{align} $
Jadi, nilai $ k=3 . \heartsuit $
$y=x^2-(k+2)x+2k \Rightarrow c=0^2-(k+2).0+2k $
$ \Rightarrow c = 2k. $
$\clubsuit \, $ Parabola memotong sumbu X di (a,0) dan (b,0) , artinya a dan b adalah akar-akar dari $ x^2-(k+2)x+2k = 0 \, $ , sehingga berlaku rumus penjumlahan akar-akar :
$a+b = \frac{-b}{a} = \frac{-(-(k+2))}{1} \Leftrightarrow a+b = k + 2 \, $ ...pers(i)
$\clubsuit \,$ Barisan aritmatika $a+2, \, c, \, $ dan $ a + 2b \, $ , selisihnya sama :
$\begin{align} (c) - (a+2) & = (a+2b) - (c) \\ 2c & = (a+2b) + (a+2) \\ 2c & = 2(a+b) + 2 \\ \text{(gunakan pers(i) dan } & \, c = 2k )\\ 2.(2k) & = 2(k+2) + 2 \\ 4k & = 2k + 6 \\ 2k & = 6 \\ k & = \frac{6}{2} = 3 \end{align} $
Jadi, nilai $ k=3 . \heartsuit $
Nomor 15
Kode kupon hadiah untuk belanja pada suatu toko swalayan berbentuk bilangan yang disusun dari angka 1, 3, 3, 6, 9. Jika kupon-kupon tersebut disusun
berdasarkan kodenya mulai dari yang terkecil sampai dengan yang terbesar, maka kupon dengan kode kurang daripada 63000 ada sebanyak ....
$\spadesuit \, $ Pilihan angkanya : 1, 3, 3, 6, 9
kode kurang daripada 63000, disusun berdasarkan puluhan ribuannya dibagi menjadi tiga kasus :
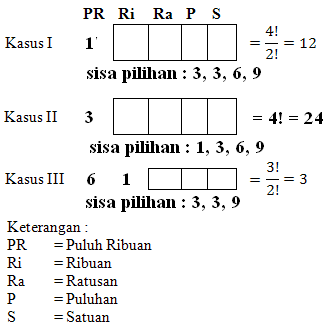
Total cara = 12 + 24 + 3 = 39 cara.
$\spadesuit \, $ Penjelasan :
Kasus I, Puluhan ribuannya angka 1 dan sisanya (Ribuan, Ratusan, Puluhan, Satuan) dipilih dari angka 3, 3, 6, 9 yaitu permutasinya sebanyak $ \frac{4!}{2!} = 12 \, $ susunan.
contohnya : 13369, 13396, 13639, dan seterusnya.
Begitu juga untuk kasus II dan III .
Jadi, total kupon sebanyak 39 kupon yang lebih kecil dari 63000. $\heartsuit $
kode kurang daripada 63000, disusun berdasarkan puluhan ribuannya dibagi menjadi tiga kasus :

Total cara = 12 + 24 + 3 = 39 cara.
$\spadesuit \, $ Penjelasan :
Kasus I, Puluhan ribuannya angka 1 dan sisanya (Ribuan, Ratusan, Puluhan, Satuan) dipilih dari angka 3, 3, 6, 9 yaitu permutasinya sebanyak $ \frac{4!}{2!} = 12 \, $ susunan.
contohnya : 13369, 13396, 13639, dan seterusnya.
Begitu juga untuk kasus II dan III .
Jadi, total kupon sebanyak 39 kupon yang lebih kecil dari 63000. $\heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.