Nomor 6
Diberikan limas $T.ABC$. Misalkan $u=\vec{TA}, v=\vec{TB}, w=\vec{TC}$. Jika $P$ titik berat $\Delta ABC$, maka $\vec{TP}=...$
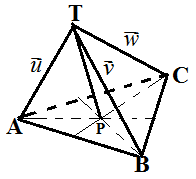

$\spadesuit \, $ Titik P adalah titik berat, sehingga:
$\vec{AP}=\frac{2}{3}\vec{AD} \, $ dan $\vec{BD} : \vec{DC} = 1 : 1$
$\spadesuit \, $ Menentukan vektor $\vec{TD}$ dari gambar berikut:
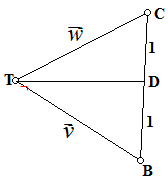
$\vec{TD}=\frac{1.\vec{v}+1.\vec{w}}{1+1} = \frac{\vec{v}+\vec{w}}{2} $
$\spadesuit \, $ Menentukan vektor $\vec{AD}$ dan $\vec{AP}$ :
$\begin{align*} \vec{AD}&=\vec{AT}+\vec{TD} \\ &=-\vec{u}+ \left( \frac{\vec{v}+\vec{w}}{2} \right) \\ \vec{AD}&= \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \\ \vec{AP}&=\frac{2}{3}\vec{AD} \\ \vec{AP}&=\frac{2}{3}.\left( \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \right) \\ \vec{AP}&=\frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \end{align*}$
$\spadesuit \, $ Menentukan vektor $\vec{TP}$ :
$\begin{align*} \vec{TP}&=\vec{TA}+\vec{AP} \\ &=\vec{u}+ \frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \\ &=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}) \end{align*}$
Jadi, $\vec{TP}=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}). \heartsuit $
$\vec{AP}=\frac{2}{3}\vec{AD} \, $ dan $\vec{BD} : \vec{DC} = 1 : 1$
$\spadesuit \, $ Menentukan vektor $\vec{TD}$ dari gambar berikut:

$\vec{TD}=\frac{1.\vec{v}+1.\vec{w}}{1+1} = \frac{\vec{v}+\vec{w}}{2} $
$\spadesuit \, $ Menentukan vektor $\vec{AD}$ dan $\vec{AP}$ :
$\begin{align*} \vec{AD}&=\vec{AT}+\vec{TD} \\ &=-\vec{u}+ \left( \frac{\vec{v}+\vec{w}}{2} \right) \\ \vec{AD}&= \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \\ \vec{AP}&=\frac{2}{3}\vec{AD} \\ \vec{AP}&=\frac{2}{3}.\left( \frac{\vec{v}+\vec{w}-2\vec{u}}{2} \right) \\ \vec{AP}&=\frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \end{align*}$
$\spadesuit \, $ Menentukan vektor $\vec{TP}$ :
$\begin{align*} \vec{TP}&=\vec{TA}+\vec{AP} \\ &=\vec{u}+ \frac{1}{3}(\vec{v}+\vec{w}-2\vec{u}) \\ &=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}) \end{align*}$
Jadi, $\vec{TP}=\frac{1}{3}(\vec{u}+\vec{v}+\vec{w}). \heartsuit $
Nomor 7
Diketahui suatu parabola simetris terhadap garis $x=-2$, dan garis singgung parabola tersebut di titik (0, 1) sejajar garis $4x+y=4$.
Titik puncak parabola tersebut adalah ...
$\clubsuit \, $ Misalkan persamaan fungsinya , $y=f(x)=ax^2+bx+c$. Dengan titik puncak $(x_p,y_p) \, \,$ :
$x_p=-\frac{b}{2a}$ dan $y_p=f(x_p)$ , serta $f^\prime(x)=2ax+b$.
$\clubsuit \, $ Sumbu simetrinya $x=-2 \,$ dengan $ x=x_p$ :
$x=x_p \Leftrightarrow -2=-\frac{b}{2a} \Leftrightarrow b=4a \, $ ...pers(i)
$\clubsuit \, $ Garis singgung di (0,1) , artinya titik (0,1) dilalui parabola, substitusi (0,1) ke persamaan parabola:
$y=ax^2+bx+c \Leftrightarrow 1=a.0^2+b.0+c \Leftrightarrow c=1$
sehingga persamaan parabolanya menjadi : $f(x)=ax^2+bx+1$
$\clubsuit \, $ Gradien garis singgung sejajar dengan garis $4x+y=4$, artinya gradiennya sama dengan gradien garis $4x+y=4\, $ yaitu $m=-4$.
$\clubsuit \, $ Menentukan gradien garis singgung di titik (0,1):
$m=f^\prime(x) \Leftrightarrow -4=f^\prime(0) \Leftrightarrow -4=2a.0+b \Leftrightarrow b=-4.$
Pers(i) : $b=4a \Leftrightarrow -4=4a \Leftrightarrow a=-1$ .
Persamaan parabolanya menjadi : $f(x)=-x^2-4x+1$
$\clubsuit \, $ Menentukan titik puncak:
$x_p=-2 \Rightarrow y_p=f(x_p)=f(-2)=-(-2)^2-4.(-2)+1=5$.
Jadi, titik puncaknya adalah $(x_p,y_p)=(-2,5). \heartsuit$
$\clubsuit \, $ Sumbu simetrinya $x=-2 \,$ dengan $ x=x_p$ :
$x=x_p \Leftrightarrow -2=-\frac{b}{2a} \Leftrightarrow b=4a \, $ ...pers(i)
$\clubsuit \, $ Garis singgung di (0,1) , artinya titik (0,1) dilalui parabola, substitusi (0,1) ke persamaan parabola:
$y=ax^2+bx+c \Leftrightarrow 1=a.0^2+b.0+c \Leftrightarrow c=1$
sehingga persamaan parabolanya menjadi : $f(x)=ax^2+bx+1$
$\clubsuit \, $ Gradien garis singgung sejajar dengan garis $4x+y=4$, artinya gradiennya sama dengan gradien garis $4x+y=4\, $ yaitu $m=-4$.
$\clubsuit \, $ Menentukan gradien garis singgung di titik (0,1):
$m=f^\prime(x) \Leftrightarrow -4=f^\prime(0) \Leftrightarrow -4=2a.0+b \Leftrightarrow b=-4.$
Pers(i) : $b=4a \Leftrightarrow -4=4a \Leftrightarrow a=-1$ .
Persamaan parabolanya menjadi : $f(x)=-x^2-4x+1$
$\clubsuit \, $ Menentukan titik puncak:
$x_p=-2 \Rightarrow y_p=f(x_p)=f(-2)=-(-2)^2-4.(-2)+1=5$.
Jadi, titik puncaknya adalah $(x_p,y_p)=(-2,5). \heartsuit$
Nomor 8
Semua nilai $a$ sehingga $f(x)=log(4^x+a.2^x+a+3)$ selalu bernilai real adalah ...
$\spadesuit \, $ Syarat kogaritma : ${}^{a}log{b} \, $ syaratnya $a>0, a\neq 1, b>0$.
$\spadesuit \, $ Bentuk $ax^2+bx+c>0 $ adalah definit positif, syaratnya : $a>0\,$ dan $D<0$.
$\spadesuit \, \, f(x)=log(4^x+a.2^x+a+3) \, $ syaratnya ;
$4^x+a.2^x+a+3>0 \Leftrightarrow (2^x)^2+a.2^x+(a+3)>0$ $ \Leftrightarrow (p)^2+ap+(a+3)>0 \, \, \,$ dengan $\, p=2^x>0$
$\spadesuit \, $ Bentuk $(p)^2+ap+(a+3)>0 \, $ termasuk definit positif dengan $a=1,b=a,c=a+3 \, ,$ syaratnya:
$\begin{align*} a&=1>0 \, \, \text{(benar)}\\ D&<0 \Leftrightarrow b^2-4ac<0 \\ a^2-4.1.(a+3)&<0 \\ a^2-4a-12&<0 \\ (a+2)(a-6)&<0 \\ a=-2 \, & \text{atau} \, a=6 \end{align*}$

$\text{HP}_1=\{ -2< a < 6 \} $
$\spadesuit \, $ Nilai $p=2^x \, $ selalu positif , sehingga untuk $a$ positif maka nilai $(p)^2+ap+(a+3) \, \, $ juga positif . $\text{HP}_2=\{ a \geq 0 \} $
Jadi, $\text{HP}=\text{HP}_1 \cup \text{HP}_2 = \{ a > -2 \}. \heartsuit$
$\spadesuit \, $ Bentuk $ax^2+bx+c>0 $ adalah definit positif, syaratnya : $a>0\,$ dan $D<0$.
$\spadesuit \, \, f(x)=log(4^x+a.2^x+a+3) \, $ syaratnya ;
$4^x+a.2^x+a+3>0 \Leftrightarrow (2^x)^2+a.2^x+(a+3)>0$ $ \Leftrightarrow (p)^2+ap+(a+3)>0 \, \, \,$ dengan $\, p=2^x>0$
$\spadesuit \, $ Bentuk $(p)^2+ap+(a+3)>0 \, $ termasuk definit positif dengan $a=1,b=a,c=a+3 \, ,$ syaratnya:
$\begin{align*} a&=1>0 \, \, \text{(benar)}\\ D&<0 \Leftrightarrow b^2-4ac<0 \\ a^2-4.1.(a+3)&<0 \\ a^2-4a-12&<0 \\ (a+2)(a-6)&<0 \\ a=-2 \, & \text{atau} \, a=6 \end{align*}$

$\text{HP}_1=\{ -2< a < 6 \} $
$\spadesuit \, $ Nilai $p=2^x \, $ selalu positif , sehingga untuk $a$ positif maka nilai $(p)^2+ap+(a+3) \, \, $ juga positif . $\text{HP}_2=\{ a \geq 0 \} $
Jadi, $\text{HP}=\text{HP}_1 \cup \text{HP}_2 = \{ a > -2 \}. \heartsuit$
Nomor 9
Misalkan diberikan titik A(1, 0) dan B(0, 1) . Jika P bersifat $|\vec{PA}|:|\vec{PB}|=\sqrt{m}:\sqrt{n}$ , maka P terletak pada
lingkaran dengan persamaan ...
$\clubsuit \, $ Misalkan titik $P(x,y)$, panjang $\vec{PA}$ dan $\vec{PB}$ :
$|\vec{PA}|=\sqrt{(x-1)^2+(y-0)^2}=\sqrt{(x-1)^2+y^2}$
$|\vec{PB}|=\sqrt{(x-0)^2+(y-1)^2}=\sqrt{x^2+(y-1)^2}$
$\clubsuit \, $ Kuadratkan bentuk $|\vec{PA}|:|\vec{PB}|=\sqrt{m}:\sqrt{n}$
$\begin{align*} |\vec{PA}|:|\vec{PB}|&=\sqrt{m}:\sqrt{n} \\ \left( \frac{|\vec{PA}|}{|\vec{PB}|} \right)^2 &=\left( \frac{\sqrt{m}}{\sqrt{n}} \right)^2 \\ \left( \frac{\sqrt{(x-1)^2+y^2}}{\sqrt{x^2+(y-1)^2}} \right)^2 &=\left( \frac{\sqrt{m}}{\sqrt{n}} \right)^2 \\ \left( \frac{(x-1)^2+y^2}{x^2+(y-1)^2} \right) &=\left( \frac{m}{n} \right) \\ n[x^2+y^2+1-2x]&=m[x^2+y^2+1-2y] \\ n(x^2+y^2+1)-n.2x&=m(x^2+y^2+1)-m.2y \\ n(x^2+y^2+1)-m(x^2+y^2+1)&=2nx-2my \\ (n-m)(x^2+y^2+1)&=2(nx-my) \end{align*}$
Jadi, persamaan lingkarannya: $(n-m)(x^2+y^2+1)=2(nx-my) \, \heartsuit $
$|\vec{PA}|=\sqrt{(x-1)^2+(y-0)^2}=\sqrt{(x-1)^2+y^2}$
$|\vec{PB}|=\sqrt{(x-0)^2+(y-1)^2}=\sqrt{x^2+(y-1)^2}$
$\clubsuit \, $ Kuadratkan bentuk $|\vec{PA}|:|\vec{PB}|=\sqrt{m}:\sqrt{n}$
$\begin{align*} |\vec{PA}|:|\vec{PB}|&=\sqrt{m}:\sqrt{n} \\ \left( \frac{|\vec{PA}|}{|\vec{PB}|} \right)^2 &=\left( \frac{\sqrt{m}}{\sqrt{n}} \right)^2 \\ \left( \frac{\sqrt{(x-1)^2+y^2}}{\sqrt{x^2+(y-1)^2}} \right)^2 &=\left( \frac{\sqrt{m}}{\sqrt{n}} \right)^2 \\ \left( \frac{(x-1)^2+y^2}{x^2+(y-1)^2} \right) &=\left( \frac{m}{n} \right) \\ n[x^2+y^2+1-2x]&=m[x^2+y^2+1-2y] \\ n(x^2+y^2+1)-n.2x&=m(x^2+y^2+1)-m.2y \\ n(x^2+y^2+1)-m(x^2+y^2+1)&=2nx-2my \\ (n-m)(x^2+y^2+1)&=2(nx-my) \end{align*}$
Jadi, persamaan lingkarannya: $(n-m)(x^2+y^2+1)=2(nx-my) \, \heartsuit $
Nomor 10
Diketahui $a , a+b $, dan $a+5b$ merupakan 3 suku pertama suatu barisan geometri. Jika $a, a+b, x, y$, dan $z$ merupakan 5 suku pertama
suatu barisan aritmetika dan $x+y+z=-15$, maka suku ke-10 barisan aritmetika tersebut adalah ...
$\spadesuit \, $ Barisan geometri (rasio sama): $a, a+b, a+5b$
$\frac{u_2}{u_1}=\frac{u_3}{u_2} \Leftrightarrow (u_2)^2=u_1.u_3 \Leftrightarrow (a+b)^2=a.(a+5b)$
$ \Leftrightarrow b^2-3ab=0 \Leftrightarrow b(b-3a)=0 $
$\Leftrightarrow b=0 \, \text{(tidak memenuhi)} \, \text{atau} \, b=3a \, \text{...pers(i)} \, \text{(memenuhi)}$
$\spadesuit \, $ Barisan aritmetika (beda/selisih sama): $a, a+b, x, y$, dan $z$
$y-x=z-y \Leftrightarrow x+z=2y \, \, \text{...pers(ii)}$
$\spadesuit \, $ Substitusi pers(ii) ke $x+y+z=-15$
$x+y+z=-15 \Leftrightarrow (x+z)+y=-15 \Leftrightarrow 2y+y=-15 \Leftrightarrow y=-5$
$\spadesuit \, y \, $ adalah suku ke-4 pada barisan aritmatika, sehingga $u_4=-5$
$u_4=-5 \Leftrightarrow a+3b=-5 \Leftrightarrow a+3(3a)=-5 \Leftrightarrow a=-\frac{1}{2}$
Pers(i) : $b=3a \Leftrightarrow b=3.-\frac{1}{2} \Leftrightarrow b=-\frac{3}{2}$
$\spadesuit \, $ Menentukan $u_{10} \, $ pada barisan aritmatika :
$\begin{align*} u_{10}&=a+9b \\ &=-\frac{1}{2} + 9. \left( -\frac{3}{2} \right) \\ u_{10}&= -\frac{28}{2} = -14 \end{align*}$
Jadi, suku ke-10 : $u_{10}=-14. \heartsuit $
$\frac{u_2}{u_1}=\frac{u_3}{u_2} \Leftrightarrow (u_2)^2=u_1.u_3 \Leftrightarrow (a+b)^2=a.(a+5b)$
$ \Leftrightarrow b^2-3ab=0 \Leftrightarrow b(b-3a)=0 $
$\Leftrightarrow b=0 \, \text{(tidak memenuhi)} \, \text{atau} \, b=3a \, \text{...pers(i)} \, \text{(memenuhi)}$
$\spadesuit \, $ Barisan aritmetika (beda/selisih sama): $a, a+b, x, y$, dan $z$
$y-x=z-y \Leftrightarrow x+z=2y \, \, \text{...pers(ii)}$
$\spadesuit \, $ Substitusi pers(ii) ke $x+y+z=-15$
$x+y+z=-15 \Leftrightarrow (x+z)+y=-15 \Leftrightarrow 2y+y=-15 \Leftrightarrow y=-5$
$\spadesuit \, y \, $ adalah suku ke-4 pada barisan aritmatika, sehingga $u_4=-5$
$u_4=-5 \Leftrightarrow a+3b=-5 \Leftrightarrow a+3(3a)=-5 \Leftrightarrow a=-\frac{1}{2}$
Pers(i) : $b=3a \Leftrightarrow b=3.-\frac{1}{2} \Leftrightarrow b=-\frac{3}{2}$
$\spadesuit \, $ Menentukan $u_{10} \, $ pada barisan aritmatika :
$\begin{align*} u_{10}&=a+9b \\ &=-\frac{1}{2} + 9. \left( -\frac{3}{2} \right) \\ u_{10}&= -\frac{28}{2} = -14 \end{align*}$
Jadi, suku ke-10 : $u_{10}=-14. \heartsuit $
kok sulit to mas ,bikin yang sederhana bisa nggak ?
BalasHapus