Nomor 1
Banyaknya akar real $f(t)=t^9-t$ adalah ... buah.
$\clubsuit \, $ Bentuk pemfaktoran :
$p^2-q^2=(p-q)(p+q)\, $ atau $\, p^n-1=(p^{n/2}-1)(p^{n/2}+1)$
dengan $n$ genap
$\clubsuit \, $ Untuk menentukan akar-akarnya, maka $f(t)=0$
$\begin{align} f(t)&=0 \\ t^9-t&=0 \\ t(t^8-1)&=0 \\ t(t^4-1)(t^4+1)&=0 \\ t(t^2-1)(t^2+1)(t^4+1)&=0 \\ t(t-1)(t+1)(t^2+1)(t^4+1)&=0 \end{align}$
$\clubsuit \,$ Sehingga akar-akarnya:
$t=0,t=1,t=-1$ dan $t^2=-1$ (tidak real) serta $t^4=-1$ (tidak real).
$\clubsuit \, $ Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. $ \, \heartsuit $
$p^2-q^2=(p-q)(p+q)\, $ atau $\, p^n-1=(p^{n/2}-1)(p^{n/2}+1)$
dengan $n$ genap
$\clubsuit \, $ Untuk menentukan akar-akarnya, maka $f(t)=0$
$\begin{align} f(t)&=0 \\ t^9-t&=0 \\ t(t^8-1)&=0 \\ t(t^4-1)(t^4+1)&=0 \\ t(t^2-1)(t^2+1)(t^4+1)&=0 \\ t(t-1)(t+1)(t^2+1)(t^4+1)&=0 \end{align}$
$\clubsuit \,$ Sehingga akar-akarnya:
$t=0,t=1,t=-1$ dan $t^2=-1$ (tidak real) serta $t^4=-1$ (tidak real).
$\clubsuit \, $ Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. $ \, \heartsuit $
Nomor 2
Jika $C(t)=\frac{1}{t} \int \limits_0^t \left( f(s)+g(s) \right) ds$ dan $\displaystyle \lim_{a \to 0} \frac{C(t_0+a)-C(t_0)}{a}=0$,
maka $C(t_0)=...$
$\spadesuit \, $ Misal hasil integral $f(s)$ adalah $F(s)$ dan $g(s)$ adalah $G(s)$.
$\begin{align} C(t)&=\frac{1}{t} \int \limits_0^t \left( f(s)+g(s) \right) ds \\ C(t)&=\frac{1}{t} \left[ F(s)+G(s) \right]_0^t \\ C(t)&=\frac{1}{t} \left[ F(t)+G(t)-F(0)-G(0) \right] \\ t.C(t)&=\left[ F(t)+G(t)-F(0)-G(0) \right] \, \text{...pers(i)} \end{align}$
$\spadesuit \, F(0)$ dan $G(0)$ adalah konstanta, sehingga turunannya sama dengan nol, dan turunan $F(t),G(t)$ berturut-turut adalah $f(t)$ dan $g(t)$
$\spadesuit \, $ Turunan pers(i) terhadap $t$:
$\, \, \, 1.C(t)+t.C^\prime(t)=f(t)+g(t)$ ...pers(ii)
$\spadesuit \, $ Menyelesaikan limit dengan cara diturunkan terhadap $a$:
$\begin{align} \displaystyle \lim_{a \to 0} \frac{C(t_0+a)-C(t_0)}{a}&=0 \\ \displaystyle \lim_{a \to 0} \frac{C^\prime(t_0+a)}{1}&=0 \\ C^\prime(t_0+0) &= 0 \\ C^\prime(t_0) &= 0 \, \text{....pers(iii)} \end{align}$
$\spadesuit \, $ Gunakan pers(iii) dan substitusikan $t=t_0$ ke pers (ii) :
$\begin{align} 1.C(t)+t.C^\prime(t)&=f(t)+g(t) \\ C(t_0)+t_0.C^\prime(t_0)&=f(t_0)+g(t_0) \\ C(t_0)+t_0.0&=f(t_0)+g(t_0) \\ C(t_0)&=f(t_0)+g(t_0) \end{align}$
Jadi, $C(t_0)=f(t_0)+g(t_0) . \, \heartsuit $
$\begin{align} C(t)&=\frac{1}{t} \int \limits_0^t \left( f(s)+g(s) \right) ds \\ C(t)&=\frac{1}{t} \left[ F(s)+G(s) \right]_0^t \\ C(t)&=\frac{1}{t} \left[ F(t)+G(t)-F(0)-G(0) \right] \\ t.C(t)&=\left[ F(t)+G(t)-F(0)-G(0) \right] \, \text{...pers(i)} \end{align}$
$\spadesuit \, F(0)$ dan $G(0)$ adalah konstanta, sehingga turunannya sama dengan nol, dan turunan $F(t),G(t)$ berturut-turut adalah $f(t)$ dan $g(t)$
$\spadesuit \, $ Turunan pers(i) terhadap $t$:
$\, \, \, 1.C(t)+t.C^\prime(t)=f(t)+g(t)$ ...pers(ii)
$\spadesuit \, $ Menyelesaikan limit dengan cara diturunkan terhadap $a$:
$\begin{align} \displaystyle \lim_{a \to 0} \frac{C(t_0+a)-C(t_0)}{a}&=0 \\ \displaystyle \lim_{a \to 0} \frac{C^\prime(t_0+a)}{1}&=0 \\ C^\prime(t_0+0) &= 0 \\ C^\prime(t_0) &= 0 \, \text{....pers(iii)} \end{align}$
$\spadesuit \, $ Gunakan pers(iii) dan substitusikan $t=t_0$ ke pers (ii) :
$\begin{align} 1.C(t)+t.C^\prime(t)&=f(t)+g(t) \\ C(t_0)+t_0.C^\prime(t_0)&=f(t_0)+g(t_0) \\ C(t_0)+t_0.0&=f(t_0)+g(t_0) \\ C(t_0)&=f(t_0)+g(t_0) \end{align}$
Jadi, $C(t_0)=f(t_0)+g(t_0) . \, \heartsuit $
Nomor 3
Banyak cara menyusun 4 buku matematika, 3 buku fisika, dan 2 buku kimia sehingga buku-buku sejenis dalam satu kelompok adalah...
$\clubsuit \, $ Ada 3 jenis buku (mat, fis, kim) yang akan disusun dengan susunan sebanyak $3!$ cara = 6 cara
$\clubsuit \, $ Masing-masing buku berkelompok dengan penyusunan :
4 mat $\Rightarrow \, $ 4! cara = 24 cara
3 fis $\Rightarrow \, $ 3! cara = 6 cara
2 kim $\Rightarrow \, $ 2! cara = 2 cara
$\clubsuit \, $ Jadi total penyusunan buku-buku tersebut :
3! . (4! . 3!. 2!) = 6 . 24. 6. 2 = 1728 cara. $\heartsuit $
$\clubsuit \, $ Masing-masing buku berkelompok dengan penyusunan :
4 mat $\Rightarrow \, $ 4! cara = 24 cara
3 fis $\Rightarrow \, $ 3! cara = 6 cara
2 kim $\Rightarrow \, $ 2! cara = 2 cara
$\clubsuit \, $ Jadi total penyusunan buku-buku tersebut :
3! . (4! . 3!. 2!) = 6 . 24. 6. 2 = 1728 cara. $\heartsuit $
Nomor 4
Jika $3sinx+4cosy=5$, maka nilai maksimum $3cosx+4siny$ adalah ...
$\spadesuit \, $ Kuadratkan persamaan $3sinx+4cosy=5$:
$\begin{align} (3sinx+4cosy)^2&=5^2 \\ 9sin^2x+16cos^2y+24sinxcosy&=25 \, \, (sin^2z+cos^2z=1 )\\ 9(1-cos^2x)+16(1-sin^2y)+24sinxcosy&=25 \\ 9-9cos^2x+16-16sin^2y+24sinxcosy&=25 \\ 9cos^2x+16sin^2y&=24sinxcosy \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Misalkan $f=3cosx+4siny$, dikuadratkan:
$\begin{align} f^2&=(3cosx+4siny )^2 \\ f^2&=9cos^2x+16sin^2y+24cosxsiny \, \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers (i) ke pers(ii) :
$\begin{align} f^2&=9cos^2x+16sin^2y+24cosxsiny \\ &=24sinxcosy + 24cosxsiny \\ &=24(sinxcosy + cosxsiny) \\ f^2&=24sin(x+y) \end{align}$
$\spadesuit \, $ Nilai maksimum dari , $y=Asinf(x) \Rightarrow y_{max}=|A|$ :
$\begin{align} f^2&=24sin(x+y) \\ f^2_{max}&=|24| \\ f^2_{max}&=24 \\ f_{max}&=\sqrt{24} \\ f_{max}&=2\sqrt{6} \end{align}$
Jadi, nilai maksimum dari $3cosx+4siny=2\sqrt{6}. \heartsuit $
$\begin{align} (3sinx+4cosy)^2&=5^2 \\ 9sin^2x+16cos^2y+24sinxcosy&=25 \, \, (sin^2z+cos^2z=1 )\\ 9(1-cos^2x)+16(1-sin^2y)+24sinxcosy&=25 \\ 9-9cos^2x+16-16sin^2y+24sinxcosy&=25 \\ 9cos^2x+16sin^2y&=24sinxcosy \, \, \, \text{...pers(i)} \end{align}$
$\spadesuit \, $ Misalkan $f=3cosx+4siny$, dikuadratkan:
$\begin{align} f^2&=(3cosx+4siny )^2 \\ f^2&=9cos^2x+16sin^2y+24cosxsiny \, \, \, \text{...pers(ii)} \end{align}$
$\spadesuit \, $ Substitusi pers (i) ke pers(ii) :
$\begin{align} f^2&=9cos^2x+16sin^2y+24cosxsiny \\ &=24sinxcosy + 24cosxsiny \\ &=24(sinxcosy + cosxsiny) \\ f^2&=24sin(x+y) \end{align}$
$\spadesuit \, $ Nilai maksimum dari , $y=Asinf(x) \Rightarrow y_{max}=|A|$ :
$\begin{align} f^2&=24sin(x+y) \\ f^2_{max}&=|24| \\ f^2_{max}&=24 \\ f_{max}&=\sqrt{24} \\ f_{max}&=2\sqrt{6} \end{align}$
Jadi, nilai maksimum dari $3cosx+4siny=2\sqrt{6}. \heartsuit $
Nomor 5
Diberikan kubus $ABCD.EFGH$ dengan panjang rusuk $3p$. Titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD sehingga $BP=GQ=DR=p$.
Misalkan $\beta$ adalah irisan bidang yang melalui P, Q, dan R. Luas alas yang berada di bawah bidang $\beta$ adalah ... $p^2$.
$\clubsuit \, $ Gambar bidang irisan (bidang $\beta$):


$\clubsuit \, $ Bidang alas di bawah bidang $\beta$
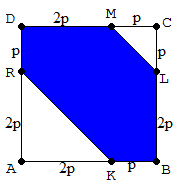
$\begin{align*} L_{\text{alas}}&=L_{ABCD}-(L_{AKR}+L_{LCM}) \\ &= (3p)^2-(\frac{1}{2}.2p.2p+\frac{1}{2}.p.p) \\ L_{\text{alas}}&=9p^2-\frac{5}{2}p^2 = \frac{13}{2}p^2 \end{align*}$
$\clubsuit \, $ Sehingga:
$\frac{L_{\text{alas}}}{L_{ABCD}}=\frac{\frac{13}{2}p^2}{9p^2}=\frac{13}{18}$
Jadi, $ L_{\text{alas}} = \frac{13}{18}L_{ABCD}. \heartsuit$


$\clubsuit \, $ Bidang alas di bawah bidang $\beta$

$\begin{align*} L_{\text{alas}}&=L_{ABCD}-(L_{AKR}+L_{LCM}) \\ &= (3p)^2-(\frac{1}{2}.2p.2p+\frac{1}{2}.p.p) \\ L_{\text{alas}}&=9p^2-\frac{5}{2}p^2 = \frac{13}{2}p^2 \end{align*}$
$\clubsuit \, $ Sehingga:
$\frac{L_{\text{alas}}}{L_{ABCD}}=\frac{\frac{13}{2}p^2}{9p^2}=\frac{13}{18}$
Jadi, $ L_{\text{alas}} = \frac{13}{18}L_{ABCD}. \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.