Nomor 6
Diketahui matriks $A$ berukuran 3 x 3 dan memenuhi $A\left( \begin{matrix}1 \\ 2 \\ 1 \end{matrix}\right) = \left( \begin{matrix}2 \\ 2 \\ 2 \end{matrix}\right) $
dan $A\left( \begin{matrix}1 \\ 2 \\ 3 \end{matrix}\right) = \left( \begin{matrix}2 \\ 4 \\ 2 \end{matrix}\right) \, \, \, $.
Jika $x=\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right)$ , maka $Ax= ...$
Untuk penyelesaian soal ini, kita tidak mencari matriks $A$ , melainkan memodifikasi setiap persamaan dengan mengalikan bilangan tertentu , misalkan $m$ dan $n$ .
Ini dilakukan karena akan lebih sulit dan ribet untuk menemukan matriks $A$ secara langsung.
$\spadesuit \, $ kalikan $m$ dan $n$ pada persamaan:
$mA\left( \begin{matrix}1 \\ 2 \\ 1 \end{matrix}\right) = m\left( \begin{matrix}2 \\ 2 \\ 2 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}m \\ 2m \\ m \end{matrix}\right) = \left( \begin{matrix}2m \\ 2m \\ 2m \end{matrix}\right)$ ...pers(i)
$nA\left( \begin{matrix}1 \\ 2 \\ 3 \end{matrix}\right) = n\left( \begin{matrix}2 \\ 4 \\ 2 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}n \\ 2n \\ 3n \end{matrix}\right) = \left( \begin{matrix}2n \\ 4n \\ 2n \end{matrix}\right)$ ...pers(ii)
$\spadesuit \, $ Jumlahkan persamaan (i) dan (ii) dan gunakan
sifat $AB+AC=A(B+C)$
$A\left( \begin{matrix}m \\ 2m \\ m \end{matrix}\right) + A\left( \begin{matrix}n \\ 2n \\ 3n \end{matrix}\right) =\left( \begin{matrix}2m \\ 2m \\ 2m \end{matrix}\right) + \left( \begin{matrix}2n \\ 4n \\ 2n \end{matrix}\right) \\ \Leftrightarrow A\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = \left( \begin{matrix}2m+2n \\ 2m+4n \\ 2m+2n \end{matrix}\right) \text{...pers(iii)}$
$\spadesuit \, $ Bentuk terakhir harus sama dengan yang ditanyakan :
$A\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) \, $ sehingga $\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = \left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right)$
Diperoleh $m+n=2$ dan $m+3n=10$ , jika diselesaikan maka solusinya $m=-2$ dan $n=4$ .
$\spadesuit \, $ Substitusikan $m=-2$ dan $n=4$ ke persamaan (iii) :
$A\left( \begin{matrix}-2+4 \\ 2.(-2)+2.4 \\ -2+3.4 \end{matrix}\right) = \left( \begin{matrix}2.(-2)+2.4 \\ 2.(-2)+4.4 \\ 2.(-2)+2.4 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) = \left( \begin{matrix}4 \\ 12 \\ 4 \end{matrix}\right) $
Jadi, $A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) = \left( \begin{matrix}4 \\ 12 \\ 4 \end{matrix}\right) . \heartsuit $
$\spadesuit \, $ kalikan $m$ dan $n$ pada persamaan:
$mA\left( \begin{matrix}1 \\ 2 \\ 1 \end{matrix}\right) = m\left( \begin{matrix}2 \\ 2 \\ 2 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}m \\ 2m \\ m \end{matrix}\right) = \left( \begin{matrix}2m \\ 2m \\ 2m \end{matrix}\right)$ ...pers(i)
$nA\left( \begin{matrix}1 \\ 2 \\ 3 \end{matrix}\right) = n\left( \begin{matrix}2 \\ 4 \\ 2 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}n \\ 2n \\ 3n \end{matrix}\right) = \left( \begin{matrix}2n \\ 4n \\ 2n \end{matrix}\right)$ ...pers(ii)
$\spadesuit \, $ Jumlahkan persamaan (i) dan (ii) dan gunakan
sifat $AB+AC=A(B+C)$
$A\left( \begin{matrix}m \\ 2m \\ m \end{matrix}\right) + A\left( \begin{matrix}n \\ 2n \\ 3n \end{matrix}\right) =\left( \begin{matrix}2m \\ 2m \\ 2m \end{matrix}\right) + \left( \begin{matrix}2n \\ 4n \\ 2n \end{matrix}\right) \\ \Leftrightarrow A\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = \left( \begin{matrix}2m+2n \\ 2m+4n \\ 2m+2n \end{matrix}\right) \text{...pers(iii)}$
$\spadesuit \, $ Bentuk terakhir harus sama dengan yang ditanyakan :
$A\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) \, $ sehingga $\left( \begin{matrix}m+n \\ 2m+2n \\ m+3n \end{matrix}\right) = \left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right)$
Diperoleh $m+n=2$ dan $m+3n=10$ , jika diselesaikan maka solusinya $m=-2$ dan $n=4$ .
$\spadesuit \, $ Substitusikan $m=-2$ dan $n=4$ ke persamaan (iii) :
$A\left( \begin{matrix}-2+4 \\ 2.(-2)+2.4 \\ -2+3.4 \end{matrix}\right) = \left( \begin{matrix}2.(-2)+2.4 \\ 2.(-2)+4.4 \\ 2.(-2)+2.4 \end{matrix}\right) \Leftrightarrow A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) = \left( \begin{matrix}4 \\ 12 \\ 4 \end{matrix}\right) $
Jadi, $A\left( \begin{matrix}2 \\ 4 \\ 10 \end{matrix}\right) = \left( \begin{matrix}4 \\ 12 \\ 4 \end{matrix}\right) . \heartsuit $
Nomor 7
Diberikan segitiga $ABC$ dengan $\angle A=\alpha$ , $\angle B= 90^o$ , dan $\angle C = \gamma$. Jika $cos\alpha = x$ , maka $cos(\alpha +2\gamma )=...$
$\clubsuit \, A$ , $B$, dan $C$ adalah sudut-sudut segitiga :
$\begin{align*} A+B+C&=180^o \\ \alpha + 90^o + \gamma &= 180^o \\ \gamma &= 90^o - \alpha \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Menyederhanakan bentuk $\alpha +2\gamma$ :
$\alpha +2\gamma=\alpha + 2(90^o - \alpha) \Leftrightarrow \alpha +2\gamma= 180^o-\alpha \, \text{...pers(ii)} $
$\clubsuit \, $ Ingat $cos(180^o-\theta)=-cos\theta$
$\begin{align*} \alpha +2\gamma&= 180^o-\alpha \\ cos(\alpha +2\gamma)&=cos(180^o-\alpha) \\ &=-cos(\alpha)\\ &=-x \end{align*}$
Jadi, $cos(\alpha +2\gamma)=-x . \, \heartsuit $
$\begin{align*} A+B+C&=180^o \\ \alpha + 90^o + \gamma &= 180^o \\ \gamma &= 90^o - \alpha \, \text{...pers(i)} \end{align*}$
$\clubsuit \, $ Menyederhanakan bentuk $\alpha +2\gamma$ :
$\alpha +2\gamma=\alpha + 2(90^o - \alpha) \Leftrightarrow \alpha +2\gamma= 180^o-\alpha \, \text{...pers(ii)} $
$\clubsuit \, $ Ingat $cos(180^o-\theta)=-cos\theta$
$\begin{align*} \alpha +2\gamma&= 180^o-\alpha \\ cos(\alpha +2\gamma)&=cos(180^o-\alpha) \\ &=-cos(\alpha)\\ &=-x \end{align*}$
Jadi, $cos(\alpha +2\gamma)=-x . \, \heartsuit $
Nomor 8
Jika garis $y=mx+k$ menyinggung lingkaran $x^2+y^2-10x+6y+24=0$ di titik (8,-4) , maka nilai $m+k$ adalah ...
$\spadesuit \, $ Substitusikan titik (8, -4) ke persamaan garis:
$y=mx+k \Leftrightarrow -4=m.8+k \Leftrightarrow k=-8m-4 \, $ ...pers(i)
$\spadesuit \, $ Menentukan unsur-unsur lingkaran:
$x^2+y^2-10x+6y+24=0 \Rightarrow A=-10 , B=6 , C=24$
Pusat : $(a,b)=\left( \frac{-A}{2}, \frac{-B}{2} \right) = \left( \frac{-(-10)}{2}, \frac{-6}{2} \right)=(5,-3)$
Jari-jari: $r=\sqrt{a^2+b^2-C}=\sqrt{5^2+(-3)^2-24} = \sqrt{10}$
Gambar:
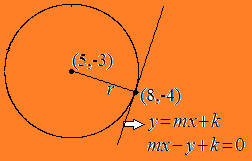
Dari gambar terlihat bahwa panjang jari-jari sama dengan jarak pusat lingkaran ke garis $mx-y+k=0$
$\spadesuit \, $ Menghitung jarak pusat lingkaran ke garis:
$\text{Jarak} =\left| \frac{m.5-(-3)+k}{\sqrt{m^2+(-1)^2}} \right| = \left| \frac{5m+k+3}{\sqrt{m^2+1}} \right|$
$\spadesuit \, $ Jarak sama dengan jari-jari dan gunakan pers(i):
$\begin{align*} \text{jarak}&=\text{jari-jari}\\ \left| \frac{5m+k+3}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{5m+(-8m-4)+3}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{-3m-1}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{-3m-1}{\sqrt{m^2+1}} \right|^2 &= \sqrt{10}^2 \, \text{(kedua ruas dikuadratkan)} \\ \frac{(-3m-1)^2}{(\sqrt{m^2+1})^2} &= 10 \\ \frac{9m^2+6m+1}{m^2+1} &= 10 \\ 9m^2+6m+1&=10m^2+10 \\ m^2-6m+9&=0\\ (m-3)^2&=0 \\ m&=3 \end{align*}$
$\spadesuit \, $ Menentukan nilai $k$ dari pers(i):
$k=-8m-4=-8(3)-4=-28$
Sehingga, $m+k=3+(-28)=-25.\heartsuit $
$y=mx+k \Leftrightarrow -4=m.8+k \Leftrightarrow k=-8m-4 \, $ ...pers(i)
$\spadesuit \, $ Menentukan unsur-unsur lingkaran:
$x^2+y^2-10x+6y+24=0 \Rightarrow A=-10 , B=6 , C=24$
Pusat : $(a,b)=\left( \frac{-A}{2}, \frac{-B}{2} \right) = \left( \frac{-(-10)}{2}, \frac{-6}{2} \right)=(5,-3)$
Jari-jari: $r=\sqrt{a^2+b^2-C}=\sqrt{5^2+(-3)^2-24} = \sqrt{10}$
Gambar:
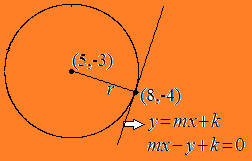
Dari gambar terlihat bahwa panjang jari-jari sama dengan jarak pusat lingkaran ke garis $mx-y+k=0$
$\spadesuit \, $ Menghitung jarak pusat lingkaran ke garis:
$\text{Jarak} =\left| \frac{m.5-(-3)+k}{\sqrt{m^2+(-1)^2}} \right| = \left| \frac{5m+k+3}{\sqrt{m^2+1}} \right|$
$\spadesuit \, $ Jarak sama dengan jari-jari dan gunakan pers(i):
$\begin{align*} \text{jarak}&=\text{jari-jari}\\ \left| \frac{5m+k+3}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{5m+(-8m-4)+3}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{-3m-1}{\sqrt{m^2+1}} \right| &= \sqrt{10} \\ \left| \frac{-3m-1}{\sqrt{m^2+1}} \right|^2 &= \sqrt{10}^2 \, \text{(kedua ruas dikuadratkan)} \\ \frac{(-3m-1)^2}{(\sqrt{m^2+1})^2} &= 10 \\ \frac{9m^2+6m+1}{m^2+1} &= 10 \\ 9m^2+6m+1&=10m^2+10 \\ m^2-6m+9&=0\\ (m-3)^2&=0 \\ m&=3 \end{align*}$
$\spadesuit \, $ Menentukan nilai $k$ dari pers(i):
$k=-8m-4=-8(3)-4=-28$
Sehingga, $m+k=3+(-28)=-25.\heartsuit $
Cara II :
$\spadesuit \, $ Konsep Dasar :
Persamaan garis singgung lingkaran $ x^2+y^2+Ax+By+C=0 $ di titik singgung $ ( x_1, y_1) $ yaitu :
$ x_1.x+y_1.y+\frac{A}{2}(x+x_1)+\frac{B}{2}(y+y_1) + C =0 $.
$\spadesuit \, $ Titik singgungnya $ (x_1,y_1) = (8, -4)$ :
$\spadesuit \, $ Menyusun PGS lingkarannya :
$\begin{align} x^2+y^2-10x+6y+24 & =0 \\ x_1.x+y_1.y-\frac{10}{2}(x+x_1)+\frac{6}{2}(y+y_1) + 24 &=0 \\ 8x - 4y-5(x+8)+3(y-4) + 24 &=0 \\ 8x - 4y-5 x - 40+3y -12 + 24 &=0 \\ 3x - y -28 &=0 \\ y = 3x -& 28 \end{align}$
Bentuk $ y = 3x - 28 $ sama dengan $ y=mx+k $ yang artinya nilai $ m = 3 $ dan $ k = -28 $.
Sehingga, $m+k=3+(-28)=-25.\heartsuit $
$\spadesuit \, $ Konsep Dasar :
Persamaan garis singgung lingkaran $ x^2+y^2+Ax+By+C=0 $ di titik singgung $ ( x_1, y_1) $ yaitu :
$ x_1.x+y_1.y+\frac{A}{2}(x+x_1)+\frac{B}{2}(y+y_1) + C =0 $.
$\spadesuit \, $ Titik singgungnya $ (x_1,y_1) = (8, -4)$ :
$\spadesuit \, $ Menyusun PGS lingkarannya :
$\begin{align} x^2+y^2-10x+6y+24 & =0 \\ x_1.x+y_1.y-\frac{10}{2}(x+x_1)+\frac{6}{2}(y+y_1) + 24 &=0 \\ 8x - 4y-5(x+8)+3(y-4) + 24 &=0 \\ 8x - 4y-5 x - 40+3y -12 + 24 &=0 \\ 3x - y -28 &=0 \\ y = 3x -& 28 \end{align}$
Bentuk $ y = 3x - 28 $ sama dengan $ y=mx+k $ yang artinya nilai $ m = 3 $ dan $ k = -28 $.
Sehingga, $m+k=3+(-28)=-25.\heartsuit $
Nomor 9
Sebuah prisma $ABCD.EFGH$ memiliki alas berbentuk persegi. Titik $T$ adalah titik tengah diagonal $HF$ . Jika $\angle EAT=\frac{\pi }{6}$ dan volume prisma tersebut $4\sqrt{6}$
, maka tinggi prisma adalah ...
$\clubsuit \, $ Misalkan panjang = lebar = $x$ dan tinggi = $t$ :
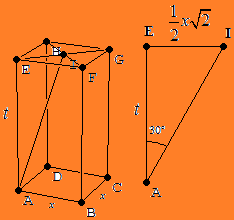
$\clubsuit \, $ Segitiga AEI :
$ EG=x\sqrt{2} \Leftrightarrow EI=\frac{1}{2}EG=\frac{1}{2}x\sqrt{2} $
$ tan(A)=\frac{EI}{EA} \Leftrightarrow tan 30^o=\frac{\frac{1}{2}x\sqrt{2}}{t} \Leftrightarrow \frac{1}{\sqrt{3}}=\frac{\frac{1}{2}x\sqrt{2}}{t} \Leftrightarrow t=\frac{1}{2}x\sqrt{6} $
$\clubsuit \, $ Menghitung tinggi ($t$) :
$\begin{align*} \text{Volume}&=\text{Luas alas} \times \text{tinggi} \\ 4\sqrt{6}&=x^2.t\\ 4\sqrt{6}&=x^2.\frac{1}{2}x\sqrt{6}\\ x^3&=8 \Leftrightarrow x=2 \end{align*}$
Jadi, tinggi : $t=\frac{1}{2}.2.\sqrt{6}=\sqrt{6} \, \heartsuit $

$\clubsuit \, $ Segitiga AEI :
$ EG=x\sqrt{2} \Leftrightarrow EI=\frac{1}{2}EG=\frac{1}{2}x\sqrt{2} $
$ tan(A)=\frac{EI}{EA} \Leftrightarrow tan 30^o=\frac{\frac{1}{2}x\sqrt{2}}{t} \Leftrightarrow \frac{1}{\sqrt{3}}=\frac{\frac{1}{2}x\sqrt{2}}{t} \Leftrightarrow t=\frac{1}{2}x\sqrt{6} $
$\clubsuit \, $ Menghitung tinggi ($t$) :
$\begin{align*} \text{Volume}&=\text{Luas alas} \times \text{tinggi} \\ 4\sqrt{6}&=x^2.t\\ 4\sqrt{6}&=x^2.\frac{1}{2}x\sqrt{6}\\ x^3&=8 \Leftrightarrow x=2 \end{align*}$
Jadi, tinggi : $t=\frac{1}{2}.2.\sqrt{6}=\sqrt{6} \, \heartsuit $
Nomor 10
Diketahui vektor $\vec{a}$ dan $\vec{b}$ membentuk sudut sebesar $\theta$ . Jika panjang proyeksi vektor $\vec{b}$ pada $\vec{a}$
sama dengan $2sin\theta$ dan panjang vektor $\vec{b}$ adalah 1, maka $tan2\theta =...$
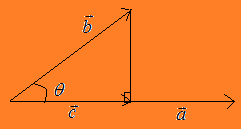
$\vec{a}.\vec{b}=|\vec{a}|.|\vec{b}| cos\theta \, $ dan $|\vec{b}|=1$ .
Panjang proyeksi vektor $\vec{b}$ pada $\vec{a}$ adalah $|\vec{c}| = 2sin\theta$ dengan rumus $|\vec{c}| = \frac{\vec{b}.\vec{a}}{ |\vec{a}| }$
$\spadesuit \, $ Menentukan nilai $tan \theta $ dan $tan 2 \theta $
$\begin{align*} |\vec{c}| &= \frac{\vec{b}.\vec{a}}{ |\vec{a}| } \\ 2sin\theta &= \frac{ |\vec{b}| . |\vec{a}| cos\theta}{ | \vec{a} | }\\ 2sin\theta &=1.cos\theta\\ \frac{sin\theta}{cos\theta} &= \frac{1}{2} \Leftrightarrow tan\theta = \frac{1}{2} \end{align*}$
$\begin{align*} tan2\theta &= \frac{2tan\theta}{1-(tan\theta)^2}\\ &= \frac{2 \frac{1}{2}}{1-\left( \frac{1}{2} \right)^2}=\frac{4}{3} \end{align*}$
Jadi, $tan2\theta=\frac{4}{3} . \, \heartsuit $
Assalamu'alaykum Kak
BalasHapusMau nanya. Untuk pembahasan no.6, kok bisa "Bentuk terakhir harus sama dengan yang ditanyakan".. Bisa dijelasin gak, Kak? Trims
Hallow dek, makasih untuk kunjungannya ke blog yg sederhana ini ya.
HapusSesuai pernyataan pembuka, tidak ditentukan matriks A dulu karna sulit. Oleh karena itu cukup modifikasi sehingga diperoleh persamaan (iii). Agar dapat jawabannya, maka pers(iiii) atau terakhir terutama ruas kiri harus sama dengan Ax (yang ditanyakan). Dengan eliminasi persamaan, diperolehlah nilai m dan n yang bisa disubstitusi ke pers(iii) untuk memperoleh jawabannya.
Gitu dek penjelasannya. Semoga bermanfaat.
Solusi soal no. 8 terlalu ribet. Soal tersebut ttg garis singgung pada lingkaran yg sudah diketahui titik singgungnya (x1,y1). Cukup pakai rumus: (x1 - a)(x - a) + (y1 - b)(y - b) = r^2.
BalasHapusHallow Pak @Amir Zulfi,
HapusTerima kasih untuk masukkannya. Ini sangat membantu pembahasan yang ada di blog dunia-informa ini sehingga akan ada banyak variasi cara yang bisa digunakan. Mohon untuk koreksinya pada pembahasan yang lainnya, terutama jika ada cara yang lebih sederhana.
Terima kasih untuk kunjungannya ke blog dunia informa ini.