Nomor 6
Sistem persamaan linier $\left\{ \begin{array}{c} x+y = 3 \\ -x+3y=1 \\ ax+4by = 4 \end{array} \right. $
mempunyai penyelesaian, jika nilai $a+2b$ adalah ...
mempunyai penyelesaian, jika nilai $a+2b$ adalah ...
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii) :
$\begin{array}{cc} x+y = 3 & \\ -x+3y=1 & + \\ \hline 4y = 4 \Rightarrow y = 1 & \end{array}$
pers(i) : $x + y = 3 \Rightarrow x + 1 = 3 \Rightarrow x = 2 $
Sehingga solusi sistem persamaan tersebut adalah (2,1).
Substitusi (2,1) ke pers(iii) :
$ax+4by = 4 \Rightarrow a.2+4b.1 = 4 \, \text{(bagi 2)} \Rightarrow a + 2b = 2 $
Jadi, nilai $a + 2b = 2 . \heartsuit $
$\begin{array}{cc} x+y = 3 & \\ -x+3y=1 & + \\ \hline 4y = 4 \Rightarrow y = 1 & \end{array}$
pers(i) : $x + y = 3 \Rightarrow x + 1 = 3 \Rightarrow x = 2 $
Sehingga solusi sistem persamaan tersebut adalah (2,1).
Substitusi (2,1) ke pers(iii) :
$ax+4by = 4 \Rightarrow a.2+4b.1 = 4 \, \text{(bagi 2)} \Rightarrow a + 2b = 2 $
Jadi, nilai $a + 2b = 2 . \heartsuit $
Nomor 7
Semua nilai $x$ yang memenuhi $\frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} \leq 0 $ adalah ...
$\clubsuit \, $ Definit positif , Syaratnya : $a > 0 $ dan Diskriminan ($D < 0 $) .
$\clubsuit \, $ Bentuk $ x^2+1 $ :
nilai $a=1 > 0$ dan $D=b^2-4ac = 0^2 - 4.1.1 = -4 < 0 $ .
Ini artinya $ x^2+1 $ adalah definit positif (akan selalu positif untuk semua $x$) .
Karena bentuknya definit positif, maka boleh dicoret tanpa membalik tanda.
Begitu juga bentuk $ x^2-x+3 $ adalah definit positif.
$\clubsuit \, $ Menyelesaikan pertidaksamaannya :
$\begin{align} \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \, \, (x^2+1) \, \text{dan} \, (x^2-x+3) \, \text{dicoret} \\ \frac{1}{(2x^2-5x-3)} & \leq 0 \\ \frac{1}{(2x +1)(x - 3)} & \leq 0 \\ x = - \frac{1}{2} \, & \vee \, x=3 \end{align} $
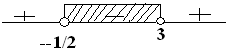
Akar penyebut tidak boleh ikut, sehingga bolong seperti pada gambar.
Jadi, solusinya adalah HP $=\{ -\frac{1}{2} < x < 3 \} . \heartsuit$
$\clubsuit \, $ Bentuk $ x^2+1 $ :
nilai $a=1 > 0$ dan $D=b^2-4ac = 0^2 - 4.1.1 = -4 < 0 $ .
Ini artinya $ x^2+1 $ adalah definit positif (akan selalu positif untuk semua $x$) .
Karena bentuknya definit positif, maka boleh dicoret tanpa membalik tanda.
Begitu juga bentuk $ x^2-x+3 $ adalah definit positif.
$\clubsuit \, $ Menyelesaikan pertidaksamaannya :
$\begin{align} \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \, \, (x^2+1) \, \text{dan} \, (x^2-x+3) \, \text{dicoret} \\ \frac{1}{(2x^2-5x-3)} & \leq 0 \\ \frac{1}{(2x +1)(x - 3)} & \leq 0 \\ x = - \frac{1}{2} \, & \vee \, x=3 \end{align} $

Akar penyebut tidak boleh ikut, sehingga bolong seperti pada gambar.
Jadi, solusinya adalah HP $=\{ -\frac{1}{2} < x < 3 \} . \heartsuit$
Cara II : Metode Suka (substitusi angka)
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \\ \frac{0^2-0+3}{(2.0^2-5.0-3)(0^2+1)} & \leq 0 \\ -1 & \leq 0 \, \, \text{(pasti benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah C, D, dan E.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \\ \frac{1^2-1+3}{(2.1^2-5.1-3)(1^2+1)} & \leq 0 \\ -\frac{1}{6} & \leq 0 \, \, \text{(pasti benar)} \end{align*}$
yang ada $x=1$ benar, opsi yang salah adalah B.
Jadi, opsi yang benar adalah A yaitu HP $=\{ -\frac{1}{2} < x < 3 \} . \heartsuit$
Metode Suka maksudnya kita memilih angka atau nilai $x$ dari pilihan, lalu disubstitusikan ke pertidaksamaannya. Metode ini hanya membutuhkan ketelitian berhitung.
$\begin{align*} \text{Pilih} \, x=0 \Rightarrow \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \\ \frac{0^2-0+3}{(2.0^2-5.0-3)(0^2+1)} & \leq 0 \\ -1 & \leq 0 \, \, \text{(pasti benar)} \end{align*}$
yang ada $x=0$ benar, opsi yang salah adalah C, D, dan E.
$\begin{align*} \text{Pilih} \, x=1 \Rightarrow \frac{x^2-x+3}{(2x^2-5x-3)(x^2+1)} & \leq 0 \\ \frac{1^2-1+3}{(2.1^2-5.1-3)(1^2+1)} & \leq 0 \\ -\frac{1}{6} & \leq 0 \, \, \text{(pasti benar)} \end{align*}$
yang ada $x=1$ benar, opsi yang salah adalah B.
Jadi, opsi yang benar adalah A yaitu HP $=\{ -\frac{1}{2} < x < 3 \} . \heartsuit$
Nomor 8
Nilai $\cos ^2(30^o) + \cos ^2(40^o) + \cos ^2(50^o) + \cos ^2(60^o) \, $ adalah ...
$\spadesuit \, $ Rumus dasar :
Sudut komplemen : $\cos x = \sin (90^o - x) $
sehingga diperoleh : $\cos 30^o = \sin 60^o \, $ dan $\cos 40^o = \sin 50^o$
Identitas : $\sin ^2 x + \cos ^2 x = 1$
$\spadesuit \, $ Mengubah soal :
$\begin{align*} & \cos ^2(30^o) + \cos ^2(40^o) + \cos ^2(50^o) + \cos ^2(60^o) \, \, \text{(sudut komplemen)} \\ & = \sin ^2(60^o) + \sin ^2(50^o) + \cos ^2(50^o) + \cos ^2(60^o) \, \, \text{(dikelompokkan)} \\ & = [\sin ^2(60^o) + \cos ^2(60^o) ] + [ \sin ^2(50^o) + \cos ^2(50^o) ] \, \, \text{(identitas)} \\ & = 1 + 1 \\ & = 2 \end{align*}$
Jadi, nilai $\cos ^2(30^o) + \cos ^2(40^o) + \cos ^2(50^o) + \cos ^2(60^o) = 2 .\heartsuit$
Sudut komplemen : $\cos x = \sin (90^o - x) $
sehingga diperoleh : $\cos 30^o = \sin 60^o \, $ dan $\cos 40^o = \sin 50^o$
Identitas : $\sin ^2 x + \cos ^2 x = 1$
$\spadesuit \, $ Mengubah soal :
$\begin{align*} & \cos ^2(30^o) + \cos ^2(40^o) + \cos ^2(50^o) + \cos ^2(60^o) \, \, \text{(sudut komplemen)} \\ & = \sin ^2(60^o) + \sin ^2(50^o) + \cos ^2(50^o) + \cos ^2(60^o) \, \, \text{(dikelompokkan)} \\ & = [\sin ^2(60^o) + \cos ^2(60^o) ] + [ \sin ^2(50^o) + \cos ^2(50^o) ] \, \, \text{(identitas)} \\ & = 1 + 1 \\ & = 2 \end{align*}$
Jadi, nilai $\cos ^2(30^o) + \cos ^2(40^o) + \cos ^2(50^o) + \cos ^2(60^o) = 2 .\heartsuit$
Nomor 9
Diagram berikut menunjukkan persentase kelulusan siswa tiga sekolah selama empat tahun.
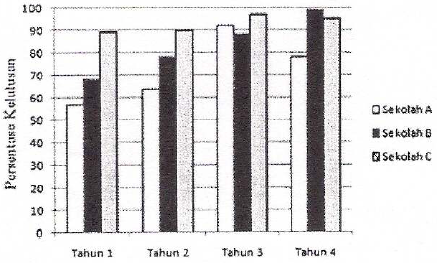
Berdasarkan diagram di atas, pernyataan berikut yang benar adalah ...

Berdasarkan diagram di atas, pernyataan berikut yang benar adalah ...
$\clubsuit \, $ Perhatikan diagram di atas :
Berdasarkan diagram, maka persentase kelulusan sekolah B selalu lebih baik dari pada tahun sebelumnya, dengan kata lain sekolah B kelulusannya selalu meningkat dari tahun sebelumnya.
Jadi, jawabannya E. $\heartsuit $
Berdasarkan diagram, maka persentase kelulusan sekolah B selalu lebih baik dari pada tahun sebelumnya, dengan kata lain sekolah B kelulusannya selalu meningkat dari tahun sebelumnya.
Jadi, jawabannya E. $\heartsuit $
Nomor 10
Jika $f(x)=x+2$ dan $g(x)=\frac{x}{x+5}$ , maka nilai $(g^{-1}of)(4)$ adalah ...
$\spadesuit \, $ Rumus invers : $g(x) = \frac{ax+b}{cx+d} \Rightarrow g^{-1}(x) = \frac{dx-b}{-cx+a}$
Sehingga , $g(x) = \frac{x}{x+5} \Rightarrow g^{-1}(x) = \frac{5x}{-x+1}$
$\spadesuit \, $ Menentukan $(g^{-1}of)(4)$
$\begin{align*} (g^{-1}of)(x) & = g^{-1}(f(x)) \\ & = g^{-1}(x+2) \\ (g^{-1}of)(x) & = \frac{5(x+2)}{-(x+2)+1} \\ \\ (g^{-1}of)(4) & = \frac{5(4+2)}{-(4+2)+1} = \frac{5.6}{-6+1} = \frac{30}{-5} = -6 \end{align*}$
Jadi, nilai $(g^{-1}of)(4) = -6. \heartsuit $
Sehingga , $g(x) = \frac{x}{x+5} \Rightarrow g^{-1}(x) = \frac{5x}{-x+1}$
$\spadesuit \, $ Menentukan $(g^{-1}of)(4)$
$\begin{align*} (g^{-1}of)(x) & = g^{-1}(f(x)) \\ & = g^{-1}(x+2) \\ (g^{-1}of)(x) & = \frac{5(x+2)}{-(x+2)+1} \\ \\ (g^{-1}of)(4) & = \frac{5(4+2)}{-(4+2)+1} = \frac{5.6}{-6+1} = \frac{30}{-5} = -6 \end{align*}$
Jadi, nilai $(g^{-1}of)(4) = -6. \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.