Nomor 6
Jika $2x-y=6, \, 2y+3z=4, $ dan $3x-z=8$ , maka nilai $5x+y+2z$ adalah ...
$\spadesuit \, $ Langsung jumlahkan ketiga persamaan tanpa menentukan nilai masing-masing
$\begin{array}{cc} 2x-y=6 & \\ 2y+3z=4 & \\ 3x-z=8 & + \\ \hline 5x+y+2z = 18 & \end{array}$
Jadi, nilai $5x+y+2z = 18 . \heartsuit $
$\begin{array}{cc} 2x-y=6 & \\ 2y+3z=4 & \\ 3x-z=8 & + \\ \hline 5x+y+2z = 18 & \end{array}$
Jadi, nilai $5x+y+2z = 18 . \heartsuit $
Nomor 7
Jika diagram batang di bawah ini memperlihatkan frekuensi kumulatif hasil tes matematika siswa kelas XII, maka persentase siswa yang
memperoleh nilai 8 adalah ...


$\clubsuit \, $ Frekuensi kumulatif siswa yang memperoleh nilai 8 adalah 22 siswa , artinya jumlah siswa yang memperoleh
nilai 2 sampai 8 ada 22 siswa, jadi bukan hanya yang mendapat nilai 8 saja.
$\clubsuit \, $ Frekuensi kumulatif siswa yang memperoleh nilai 7 adalah 19 siswa , artinya jumlah siswa yang memperoleh nilai 2 sampai 7 ada 19 siswa, jadi bukan hanya yang mendapat nilai 7 saja.
Sehingga banyak siswa yang mendapat nilia 8 saja = 22 - 19 = 3.
Total siswa ada 25 siswa.
$\clubsuit \, $ Menentukan nilai persentase :
$\begin{align} \text{Persentase nilai 8} \, & = \frac{\text{banyak siswa yang memperoleh nilai 8}}{\text{total siswa}} \times 100\% \\ & = \frac{3}{25} \times 100\% \\ & = 12 \% \end{align} $
Jadi, persentasenya adalah $ 12 \% . \heartsuit$
$\clubsuit \, $ Frekuensi kumulatif siswa yang memperoleh nilai 7 adalah 19 siswa , artinya jumlah siswa yang memperoleh nilai 2 sampai 7 ada 19 siswa, jadi bukan hanya yang mendapat nilai 7 saja.
Sehingga banyak siswa yang mendapat nilia 8 saja = 22 - 19 = 3.
Total siswa ada 25 siswa.
$\clubsuit \, $ Menentukan nilai persentase :
$\begin{align} \text{Persentase nilai 8} \, & = \frac{\text{banyak siswa yang memperoleh nilai 8}}{\text{total siswa}} \times 100\% \\ & = \frac{3}{25} \times 100\% \\ & = 12 \% \end{align} $
Jadi, persentasenya adalah $ 12 \% . \heartsuit$
Nomor 8
Budi telah mengikuti empat kali tes matematika pada semester I dengan nilai rata-rata 7,0. Jika selama setahun Budi mngikuti
delapan kali tes dengan nilai rata-rata 8,0 , maka nilai rata-rata pada semester II dibandingkan dengan semester I naik sebesar ...
$\spadesuit \, $ Permisalan :
rata-rata semester I : $\overline{x}_1 = 7 \, $ , banyak tes semester I : $n_1 = 4 $
rata-rata semester II : $\overline{x}_2 = a \, $ , banyak tes semester II : $n_2 = 8 - 4 = 4 $
rata-rata gabungannya : $\overline{x}_{\text{gb}} = 8$
$\spadesuit \, $ Rumus rata-rata gabungan : $ \overline{x}_{\text{gb}} = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2}$
$\begin{align*} \overline{x}_{\text{gb}} & = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2} \\ 8 & = \frac{4.7 + 4.a}{4 + 4} \\ 8 & = \frac{28 + 4a}{8} \\ 8.8 & = 28 + 4a \\ 4a & = 64 - 28 \\ 4a & = 36 \\ a & = \frac{36}{4} = 9 \end{align*}$
artinya nilai rata-rata semester II = 9.
sehingga kenaikkan nilai dari semester I ke semester II sebesar 9 - 7 = 2.
Jadi, nilai rata-rata pada semester II dibandingkan dengan semester I naik sebesar 2,0 . $\heartsuit$
rata-rata semester I : $\overline{x}_1 = 7 \, $ , banyak tes semester I : $n_1 = 4 $
rata-rata semester II : $\overline{x}_2 = a \, $ , banyak tes semester II : $n_2 = 8 - 4 = 4 $
rata-rata gabungannya : $\overline{x}_{\text{gb}} = 8$
$\spadesuit \, $ Rumus rata-rata gabungan : $ \overline{x}_{\text{gb}} = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2}$
$\begin{align*} \overline{x}_{\text{gb}} & = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2} \\ 8 & = \frac{4.7 + 4.a}{4 + 4} \\ 8 & = \frac{28 + 4a}{8} \\ 8.8 & = 28 + 4a \\ 4a & = 64 - 28 \\ 4a & = 36 \\ a & = \frac{36}{4} = 9 \end{align*}$
artinya nilai rata-rata semester II = 9.
sehingga kenaikkan nilai dari semester I ke semester II sebesar 9 - 7 = 2.
Jadi, nilai rata-rata pada semester II dibandingkan dengan semester I naik sebesar 2,0 . $\heartsuit$
Nomor 9
Nilai maksimum fungsi objektif (tujuan) $f(x,y)=4x+3y$ dengan kendala $2x+3y \leq 18, \, x\geq 3$ , dan $y\geq 2$ adalah ...
$\clubsuit \, $ Gambar dari kendala/batasan
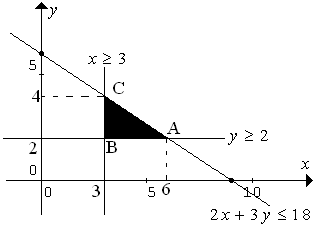
$\clubsuit \, $ Substitusikan semua titik pojok ke fungsi tujuannya :
fungsi objektif (tujuan) $f(x,y)=4x+3y$
$A(6,2) \Rightarrow f(6,2)=4.6+3.2=24+6=30$
$B(3,2) \Rightarrow f(6,2)=4.3+3.2=12+6=18$
$C(3,4) \Rightarrow f(6,2)=4.3+3.4=12+12=24$
Jadi, nilai maksimumnya adalah 30. $\heartsuit $

$\clubsuit \, $ Substitusikan semua titik pojok ke fungsi tujuannya :
fungsi objektif (tujuan) $f(x,y)=4x+3y$
$A(6,2) \Rightarrow f(6,2)=4.6+3.2=24+6=30$
$B(3,2) \Rightarrow f(6,2)=4.3+3.2=12+6=18$
$C(3,4) \Rightarrow f(6,2)=4.3+3.4=12+12=24$
Jadi, nilai maksimumnya adalah 30. $\heartsuit $
Nomor 10
Jika $AB=\left( \begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix} \right) $ , dan det($A$) = 2, maka det($BA^{-1}$) adalah ...
$\spadesuit \, $ Sifat determinan : $|PQ| = |P|.|Q| \, \, $ dan $\, |Q^{-1}| = \frac{1}{|Q|}$
$\spadesuit \, $ Menentukan determinan matriks $B$
$\begin{align*} AB & =\left( \begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix} \right) \\ |AB| & =\left| \begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix} \right| \\ |A|.|B| & = 2.2 - 0. 0 \\ 2.|B| & = 4 \\ |B| & = 2 \end{align*}$
$\spadesuit \, $ Menentukan det($BA^{-1}$)
$\begin{align*} \text{det}(BA^{-1}) & = | BA^{-1} | \\ & = | B | . |A^{-1} | \\ & = | B | . \frac{1}{|A|} \\ & = 2. \frac{1}{2} \\ & = 1 \end{align*}$
Jadi, nilai det($BA^{-1}$) = 1 . $ \heartsuit $
$\spadesuit \, $ Menentukan determinan matriks $B$
$\begin{align*} AB & =\left( \begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix} \right) \\ |AB| & =\left| \begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix} \right| \\ |A|.|B| & = 2.2 - 0. 0 \\ 2.|B| & = 4 \\ |B| & = 2 \end{align*}$
$\spadesuit \, $ Menentukan det($BA^{-1}$)
$\begin{align*} \text{det}(BA^{-1}) & = | BA^{-1} | \\ & = | B | . |A^{-1} | \\ & = | B | . \frac{1}{|A|} \\ & = 2. \frac{1}{2} \\ & = 1 \end{align*}$
Jadi, nilai det($BA^{-1}$) = 1 . $ \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.