Nomor 6
Diketahui kubus ABCD.EFGH . Jika $\alpha $ adalah sudut antara bidang ACF dan alas ABCD, maka $\tan \alpha = ...$
$\spadesuit \, $ Gambar : misalkan panjangnya 2
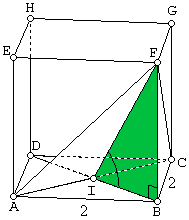
$\spadesuit \, $ Menentukan nilai $\tan \alpha $
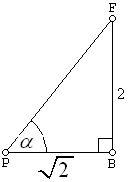
$\angle$ (ACF,ABCD) = $\angle$ (FP,PB)
$\tan \alpha = \frac{FB}{BP} = \frac{2}{\sqrt{2}} = \sqrt{2} $
Jadi, nilai $\tan \alpha = \sqrt{2} . \heartsuit $


$\spadesuit \, $ Menentukan nilai $\tan \alpha $
$\angle$ (ACF,ABCD) = $\angle$ (FP,PB)
$\tan \alpha = \frac{FB}{BP} = \frac{2}{\sqrt{2}} = \sqrt{2} $
Jadi, nilai $\tan \alpha = \sqrt{2} . \heartsuit $
Nomor 7
Lingkaran $(x-4)^2 + (y-2)^2 = 64 $ menyinggung garis $x=-4 $ di titik ...
$\clubsuit \, $ Substitusi $x=-4 $ ke persamaan
$\begin{align} (x-4)^2 + (y-2)^2 & = 64 \\ (-4-4)^2 + (y-2)^2 & = 64 \\ (-8)^2 + (y-2)^2 & = 64 \\ 64 + (y-2)^2 & = 64 \\ (y-2)^2 & = 0 \\ y-2 & = 0 \\ y & = 2 \end{align}$
Jadi, bersinggungan di titik (-4,2) . $ \heartsuit$
$\begin{align} (x-4)^2 + (y-2)^2 & = 64 \\ (-4-4)^2 + (y-2)^2 & = 64 \\ (-8)^2 + (y-2)^2 & = 64 \\ 64 + (y-2)^2 & = 64 \\ (y-2)^2 & = 0 \\ y-2 & = 0 \\ y & = 2 \end{align}$
Jadi, bersinggungan di titik (-4,2) . $ \heartsuit$
Nomor 8
Jika suku banyak $2x^3-x^2+6x-1 $ dibagi $2x-1 $ , maka sisanya adalah ...
$\spadesuit \, $ Menentukan sisa dengan cara Horner
$2x^3-x^2+6x-1 : 2x-1 $
$\begin{array}{c|ccccc} \frac{1}{2} & 2 & -1 & 6 & -1 & \\ & & 1 & 0 & 3 & + \\ \hline & 2 & 0 & 6 & 2 & \end{array} $
Jadi, sisanya adalah 2 . $ \heartsuit$
$2x^3-x^2+6x-1 : 2x-1 $
$\begin{array}{c|ccccc} \frac{1}{2} & 2 & -1 & 6 & -1 & \\ & & 1 & 0 & 3 & + \\ \hline & 2 & 0 & 6 & 2 & \end{array} $
Jadi, sisanya adalah 2 . $ \heartsuit$
Cara II
$\spadesuit \, $ Bagi biasa
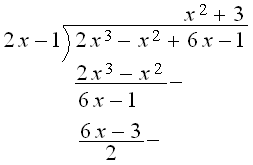
Jadi, sisanya adalah 2 . $ \heartsuit$
$\spadesuit \, $ Bagi biasa
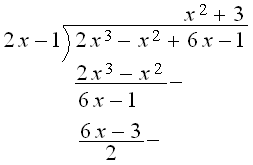
Jadi, sisanya adalah 2 . $ \heartsuit$
Cara III
$\spadesuit \, $ Teorema sisa
$\frac{f(x)}{ax-b} \rightarrow \text{Sisa} \, = f\left( \frac{b}{a} \right) $
$f(x) = 2x^3-x^2+6x-1 : 2x-1 $
$\begin{align*} \text{Sisa} \, & = f\left( \frac{1}{2} \right) \\ & = 2.\left( \frac{1}{2} \right)^3-\left( \frac{1}{2} \right)^2+6.\left( \frac{1}{2} \right)-1 \\ & = \frac{1}{4}-\frac{1}{4}+3-1 \\ & = 2 \end{align*}$
Jadi, sisanya adalah 2 . $ \heartsuit$
$\spadesuit \, $ Teorema sisa
$\frac{f(x)}{ax-b} \rightarrow \text{Sisa} \, = f\left( \frac{b}{a} \right) $
$f(x) = 2x^3-x^2+6x-1 : 2x-1 $
$\begin{align*} \text{Sisa} \, & = f\left( \frac{1}{2} \right) \\ & = 2.\left( \frac{1}{2} \right)^3-\left( \frac{1}{2} \right)^2+6.\left( \frac{1}{2} \right)-1 \\ & = \frac{1}{4}-\frac{1}{4}+3-1 \\ & = 2 \end{align*}$
Jadi, sisanya adalah 2 . $ \heartsuit$
Nomor 9
Grafik fungsi $f(x)=ax^3+bx^2-cx+20 $ turun, jika ...
$\clubsuit \, $ Syarat fungsi turun : $f^\prime (x) < 0 $
$f(x)=ax^3+bx^2-cx+20 \rightarrow f^\prime (x) = 3ax^2+2bx-c $
$f^\prime (x) < 0 \rightarrow 3ax^2+2bx-c < 0 $
ini definit negatif, syarat : $a < 0 , \, D < 0 $
$\clubsuit \, $ Menyelesaikan syarat definit negatif
$(*) \, a < 0 \rightarrow 3a < 0 \rightarrow a < 0 $
$\begin{align*} (**) \, D < 0 \rightarrow b^2-4ac & < 0 \\ (2b)^2-4.(3a).(-c) & < 0 \\ 4b^2 + 12ac & < 0 \, \, \, \text{(bagi 4)} \\ b^2 + 3ac & < 0 \end{align*}$
Jadi, $f(x) $ turun jika $ a < 0 $ dan $ b^2 + 3ac < 0 . \heartsuit $
$f(x)=ax^3+bx^2-cx+20 \rightarrow f^\prime (x) = 3ax^2+2bx-c $
$f^\prime (x) < 0 \rightarrow 3ax^2+2bx-c < 0 $
ini definit negatif, syarat : $a < 0 , \, D < 0 $
$\clubsuit \, $ Menyelesaikan syarat definit negatif
$(*) \, a < 0 \rightarrow 3a < 0 \rightarrow a < 0 $
$\begin{align*} (**) \, D < 0 \rightarrow b^2-4ac & < 0 \\ (2b)^2-4.(3a).(-c) & < 0 \\ 4b^2 + 12ac & < 0 \, \, \, \text{(bagi 4)} \\ b^2 + 3ac & < 0 \end{align*}$
Jadi, $f(x) $ turun jika $ a < 0 $ dan $ b^2 + 3ac < 0 . \heartsuit $
Nomor 10
Diketahui segitiga dengan titik sudut (-4,0), (4,0), dan ($4\cos \theta , \, 4\sin \theta$ ) untuk $0 \leq \theta \leq 2\pi $ .
Banyak nilai $\theta $ yang mungkin agar luas segitiga tersebut 13 adalah ....
$\spadesuit \, $ Titik ($x,y$) = ($4\cos \theta , \, 4\sin \theta$ ) terletak pada suatu lingkaran
$\begin{align*} x^2+y^2 & = (4\cos \theta)^2+(4\sin \theta)^2 \\ & = 16 \cos ^2 \theta + 16 \sin ^2 \theta \\ & = 16 (\cos ^2 \theta + 16 \sin ^2 \theta) \\ & = 16 \times 1 \\ x^2+y^2 & = 16 \end{align*}$
Pusat lingkaran (0,0) dan jari-jari $r=4$

$\spadesuit \, $ Menghitung tinggi segitiga
L$\Delta ABC = \frac{1}{2} $ .AB. $t \rightarrow 13 = \frac{1}{2}.8.t \rightarrow t=3\frac{1}{4}$
Ada 4 kemungkinan yang tingginya $t= 3\frac{1}{4}$ yang ada di kuadran I, II, III, IV
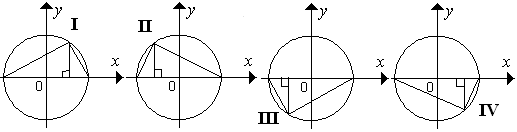
Jadi, banyak nilai $\theta $ ada 4. $\heartsuit $
$\begin{align*} x^2+y^2 & = (4\cos \theta)^2+(4\sin \theta)^2 \\ & = 16 \cos ^2 \theta + 16 \sin ^2 \theta \\ & = 16 (\cos ^2 \theta + 16 \sin ^2 \theta) \\ & = 16 \times 1 \\ x^2+y^2 & = 16 \end{align*}$
Pusat lingkaran (0,0) dan jari-jari $r=4$

$\spadesuit \, $ Menghitung tinggi segitiga
L$\Delta ABC = \frac{1}{2} $ .AB. $t \rightarrow 13 = \frac{1}{2}.8.t \rightarrow t=3\frac{1}{4}$
Ada 4 kemungkinan yang tingginya $t= 3\frac{1}{4}$ yang ada di kuadran I, II, III, IV

Jadi, banyak nilai $\theta $ ada 4. $\heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.