Nomor 1
$\displaystyle \lim_{x \to 0 } \frac{1-\cos ^2 x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} = ... $
$\clubsuit \, $ Rumus dasar
$\sin ^2x + \cos ^2 x = 1 \rightarrow 1-\cos ^2x = \sin ^2x$
$\displaystyle \lim_{x \to 0 } \frac{\sin ax}{bx} = \frac{a}{b} $
$\clubsuit \, $ Menentukan limitnya
$\begin{align*} \displaystyle \lim_{x \to 0 } \frac{1-\cos ^2 x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} & = \displaystyle \lim_{x \to 0 } \frac{\sin ^2x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} \\ & = \displaystyle \lim_{x \to 0 } \frac{\sin x}{x} . \frac{\sin x}{x} . \frac{1}{ \tan \left( x+\frac{\pi }{3} \right) } \\ & = \frac{1}{1} . \frac{1}{1} . \frac{1}{ \tan \left( 0 +\frac{\pi }{3} \right) } = \frac{1}{ \tan 60^o } \\ & = \frac{1}{ \sqrt{3} } = \frac{1}{3}\sqrt{3} \end{align*}$
Jadi, nilai $ \displaystyle \lim_{x \to 0 } \frac{1-\cos ^2 x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} = \frac{1}{3}\sqrt{3} .\heartsuit $
$\sin ^2x + \cos ^2 x = 1 \rightarrow 1-\cos ^2x = \sin ^2x$
$\displaystyle \lim_{x \to 0 } \frac{\sin ax}{bx} = \frac{a}{b} $
$\clubsuit \, $ Menentukan limitnya
$\begin{align*} \displaystyle \lim_{x \to 0 } \frac{1-\cos ^2 x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} & = \displaystyle \lim_{x \to 0 } \frac{\sin ^2x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} \\ & = \displaystyle \lim_{x \to 0 } \frac{\sin x}{x} . \frac{\sin x}{x} . \frac{1}{ \tan \left( x+\frac{\pi }{3} \right) } \\ & = \frac{1}{1} . \frac{1}{1} . \frac{1}{ \tan \left( 0 +\frac{\pi }{3} \right) } = \frac{1}{ \tan 60^o } \\ & = \frac{1}{ \sqrt{3} } = \frac{1}{3}\sqrt{3} \end{align*}$
Jadi, nilai $ \displaystyle \lim_{x \to 0 } \frac{1-\cos ^2 x}{x^2 \tan \left( x+\frac{\pi }{3} \right)} = \frac{1}{3}\sqrt{3} .\heartsuit $
Nomor 2
Di dalam kotak terdapat 1 bola biru, 6 bola merah, dan 2 bola putih. Jika diambil 7 bola tanpa pengembalian, maka peluang
banyak bola merah yang terambil dua kali banyak bola putih yang terambil adalah ...
$\spadesuit \, $ Ada bola : 1B6M2P . Akan diambil 7 bola
$ n(S) = C_7^9 = 36 $
$\spadesuit \, $ Harapannya : M = 2 $\times$ P (merah dua kali putih), dibagi dua kasus
Kasus 1 :
putih 1, maka merah 2 dan biru harus 4 (umlahnya harus 7 bola), ini tidak mungkin karena bola biru hanya ada 1.
Kasus 2 :
putih 2, merah 4 dan biru 1 (memenuhi)
$n(A) = $ 2P4M1B = $ C_2^2.C_4^6.C_1^1 = 15 $
Sehingga peluangnya : $P(A) = \frac{n(A)}{n(S)} = \frac{15}{36} = \frac{5}{12} $
Jadi, peluangnya adalah $\frac{5}{12} . \, \heartsuit $
$ n(S) = C_7^9 = 36 $
$\spadesuit \, $ Harapannya : M = 2 $\times$ P (merah dua kali putih), dibagi dua kasus
Kasus 1 :
putih 1, maka merah 2 dan biru harus 4 (umlahnya harus 7 bola), ini tidak mungkin karena bola biru hanya ada 1.
Kasus 2 :
putih 2, merah 4 dan biru 1 (memenuhi)
$n(A) = $ 2P4M1B = $ C_2^2.C_4^6.C_1^1 = 15 $
Sehingga peluangnya : $P(A) = \frac{n(A)}{n(S)} = \frac{15}{36} = \frac{5}{12} $
Jadi, peluangnya adalah $\frac{5}{12} . \, \heartsuit $
Nomor 3
Luas daerah yang dibatasi oleh kurva $y=x^2 $ , $ y=1 $ , dan $ x=2 $ adalah ...
$\clubsuit \, $ Gambarnya
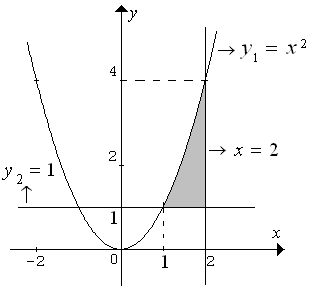
$\clubsuit \, $ Menentukan luas arsiran
$L_\text{arsiran} = \int \limits_1^2 (y_1 - y_2) dx = \int \limits_1^2 (x^2 - 1) dx $
Jadi, luasnya adalah $\int \limits_1^2 (x^2 - 1) dx . \heartsuit $

$\clubsuit \, $ Menentukan luas arsiran
$L_\text{arsiran} = \int \limits_1^2 (y_1 - y_2) dx = \int \limits_1^2 (x^2 - 1) dx $
Jadi, luasnya adalah $\int \limits_1^2 (x^2 - 1) dx . \heartsuit $
Nomor 4
$\frac{(\cos x + \sin x )^2}{(\cos x - \sin x )^2} = ...$
$\spadesuit \, $ Rumus dasar :
$\sin ^2x + \cos ^2 x = 1 $
$\sin 2x = 2\sin x \cos x $
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} \frac{(\cos x + \sin x )^2}{(\cos x - \sin x )^2} & = \frac{\sin ^2x + \cos ^2 x + 2\sin x \cos x }{\sin ^2x + \cos ^2 x - 2\sin x \cos x} \\ & = \frac{1 + 2\sin x \cos x }{1 - 2\sin x \cos x} \\ & = \frac{1 + \sin 2x }{1 - \sin 2x } \end{align}$
Jadi, $\frac{(\cos x + \sin x )^2}{(\cos x - \sin x )^2} = \frac{1 + \sin 2x }{1 - \sin 2x } . \heartsuit $
$\sin ^2x + \cos ^2 x = 1 $
$\sin 2x = 2\sin x \cos x $
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} \frac{(\cos x + \sin x )^2}{(\cos x - \sin x )^2} & = \frac{\sin ^2x + \cos ^2 x + 2\sin x \cos x }{\sin ^2x + \cos ^2 x - 2\sin x \cos x} \\ & = \frac{1 + 2\sin x \cos x }{1 - 2\sin x \cos x} \\ & = \frac{1 + \sin 2x }{1 - \sin 2x } \end{align}$
Jadi, $\frac{(\cos x + \sin x )^2}{(\cos x - \sin x )^2} = \frac{1 + \sin 2x }{1 - \sin 2x } . \heartsuit $
Nomor 5
Lingkaran $(x-3)^2+(y-4)^2=25 $ memotong sumbu X di titik $A$ dan $B$ . Jika $P$ adalah titik pusat lingkaran tersebut,
maka $\cos \angle APB = ... $
$\clubsuit \, $ Unsur-unsur lingkaran :
$(x-a)^2+(y-b)^2=r^2 $ , pusat ($a,b$) dan jari-jari $r$
$(x-3)^2+(y-4)^2=25 $ , pusat ($3,4$) dan jari-jari $r=\sqrt{25} = 5$
$\clubsuit \, $ gambarnya
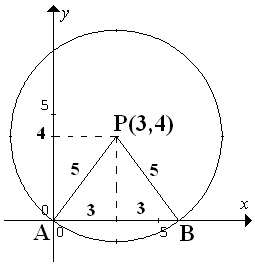
$\clubsuit \, $ Aturan cosinus pada $\Delta ABC $
$\begin{align} AB^2 & = AP^2+ BP^2 - 2.AP.BP \cos APB \\ \cos APB & = \frac{AP^2 + BP^2 - AB^2}{2.AP.BP} \\ & = \frac{5^2 + 5^2 - 6^2}{2.5.5} = \frac{25 + 25 - 36}{50} = \frac{14}{50} = \frac{7}{25} \end{align}$
Jadi, nilai $\cos APB = \frac{7}{25} . \heartsuit$
$(x-a)^2+(y-b)^2=r^2 $ , pusat ($a,b$) dan jari-jari $r$
$(x-3)^2+(y-4)^2=25 $ , pusat ($3,4$) dan jari-jari $r=\sqrt{25} = 5$
$\clubsuit \, $ gambarnya

$\clubsuit \, $ Aturan cosinus pada $\Delta ABC $
$\begin{align} AB^2 & = AP^2+ BP^2 - 2.AP.BP \cos APB \\ \cos APB & = \frac{AP^2 + BP^2 - AB^2}{2.AP.BP} \\ & = \frac{5^2 + 5^2 - 6^2}{2.5.5} = \frac{25 + 25 - 36}{50} = \frac{14}{50} = \frac{7}{25} \end{align}$
Jadi, nilai $\cos APB = \frac{7}{25} . \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.