Nomor 6
Garis g melalui titik (8, 28) dan memotong parabola $y=3x^2+x-10 $ di titik A dan B. Jika A(2, 4) dan B($x, y$), maka $x+y = ....$
$\spadesuit \, $ Deskripsi gambar
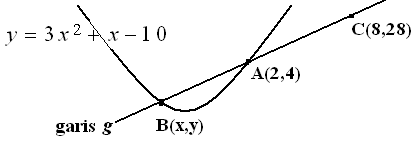
$\spadesuit \, $ Persamaan garis $g $ melalui titik ($x_1,y_1$) = (2,4) dan ($x_2,y_2$) = (8,28)
$\begin{align} \frac{y-y_1}{y_2-y_1} & = \frac{x-x_1}{x_2-x_1} \\ \frac{y-4}{28-4} & = \frac{x-2}{8-4} \\ \frac{y-4}{24} & = \frac{x-2}{4} \\ y&= 4x-4 \end{align}$
$\spadesuit \, $ Titik potong garis dan parabola
$\begin{align} y_1 & = y_2 \\ 3x^2+x-10 & = 4x-4 \\ 3x^2 - 3x - 6 & = 0 \\ x^2 - x -2 & = 0 \\ (x+1)(x-2) & = 0 \\ x=-1 & \vee x = 2 \end{align}$
$\spadesuit \, $ Substitusi nilai $x$
$x = -1 \rightarrow y = 4x-4 = 4.(-1) - 4 = -8 $
Titik B(-1,-8)
$x = 2 \rightarrow y = 4x-4 = 4.(2) - 4 = 4 $
Titik A(2,4)
Sehingga : titik B($x,y$) = B(-1,-8)
Jadi, nilai $x+y = -1 + (-8) = -9 . \heartsuit $

$\spadesuit \, $ Persamaan garis $g $ melalui titik ($x_1,y_1$) = (2,4) dan ($x_2,y_2$) = (8,28)
$\begin{align} \frac{y-y_1}{y_2-y_1} & = \frac{x-x_1}{x_2-x_1} \\ \frac{y-4}{28-4} & = \frac{x-2}{8-4} \\ \frac{y-4}{24} & = \frac{x-2}{4} \\ y&= 4x-4 \end{align}$
$\spadesuit \, $ Titik potong garis dan parabola
$\begin{align} y_1 & = y_2 \\ 3x^2+x-10 & = 4x-4 \\ 3x^2 - 3x - 6 & = 0 \\ x^2 - x -2 & = 0 \\ (x+1)(x-2) & = 0 \\ x=-1 & \vee x = 2 \end{align}$
$\spadesuit \, $ Substitusi nilai $x$
$x = -1 \rightarrow y = 4x-4 = 4.(-1) - 4 = -8 $
Titik B(-1,-8)
$x = 2 \rightarrow y = 4x-4 = 4.(2) - 4 = 4 $
Titik A(2,4)
Sehingga : titik B($x,y$) = B(-1,-8)
Jadi, nilai $x+y = -1 + (-8) = -9 . \heartsuit $
Nomor 7
Solusi pertaksamaan $2x^2+3x-9 \leq 0 $ yang bukan solusi dari pertaksamaan $2x^2-x-10 \geq 0 $ adalah ....
$\clubsuit \, $ Solusi pertidaksamaan I
$\begin{align} 2x^2+3x-9 & \leq 0 \\ (2x-3)(x+3) & \leq 0 \\ x=\frac{3}{2} & \vee x = -3 \end{align} $

$HP_1 = \{ -3 \leq x \leq \frac{3}{2} \} $
$\clubsuit \, $ Solusi pertidaksamaan II
$\begin{align} 2x^2-x-10 & \geq 0 \\ (2x-5)(x+2) & \geq 0 \\ x=\frac{5}{2} & \vee x=-2 \end{align} $
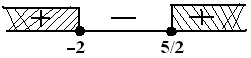
$HP_2 = \{ x \leq -2 \vee x \geq \frac{5}{2} \} $
$\clubsuit \, $ HP 1 tidak ada di HP 2 seperti gambar berikut

Sehingga : HP1 yang tidak ada di HP2 adalah $\{ -2 < x \leq \frac{3}{2} \} $
Jadi, jawabannya adalah $ \{ -2 < x \leq \frac{3}{2} \} . \heartsuit$
$\begin{align} 2x^2+3x-9 & \leq 0 \\ (2x-3)(x+3) & \leq 0 \\ x=\frac{3}{2} & \vee x = -3 \end{align} $

$HP_1 = \{ -3 \leq x \leq \frac{3}{2} \} $
$\clubsuit \, $ Solusi pertidaksamaan II
$\begin{align} 2x^2-x-10 & \geq 0 \\ (2x-5)(x+2) & \geq 0 \\ x=\frac{5}{2} & \vee x=-2 \end{align} $
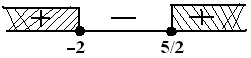
$HP_2 = \{ x \leq -2 \vee x \geq \frac{5}{2} \} $
$\clubsuit \, $ HP 1 tidak ada di HP 2 seperti gambar berikut

Sehingga : HP1 yang tidak ada di HP2 adalah $\{ -2 < x \leq \frac{3}{2} \} $
Jadi, jawabannya adalah $ \{ -2 < x \leq \frac{3}{2} \} . \heartsuit$
Nomor 8
Grafik $y=2x^3 -3x^2-12x+7 $ turun untuk $x $ yang memenuhi ....
$\spadesuit \, $ Syarat $f(x) $ turun : $f^\prime (x) < 0 $
$y=2x^3 -3x^2-12x+7 \rightarrow y^\prime = 6x^2-6x-12 $
$\begin{align*} f^\prime (x) & < 0 \\ 6x^2-6x-12 & < 0 \\ x^2 - x - 2 & < 0 \\ (x-2)(x+1) & < 0 \\ x=2 & \vee x = -1 \end{align*}$
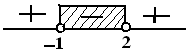
Jadi, $f(x) $ turun pada interval $ \{-1< x < 2 \} \heartsuit$
$y=2x^3 -3x^2-12x+7 \rightarrow y^\prime = 6x^2-6x-12 $
$\begin{align*} f^\prime (x) & < 0 \\ 6x^2-6x-12 & < 0 \\ x^2 - x - 2 & < 0 \\ (x-2)(x+1) & < 0 \\ x=2 & \vee x = -1 \end{align*}$

Jadi, $f(x) $ turun pada interval $ \{-1< x < 2 \} \heartsuit$
Nomor 9
Jika $f(x)=\sin ^2 3x , $ maka $\displaystyle \lim_{p \to 0} \frac{f(x+2p)-f(x)}{2p} = .... $
$\clubsuit \, $ Menentukan turunan $f(x) $
$\begin{align*} f(x) & =\sin ^2 3x \\ f^\prime (x) & = 2.\sin 3x . 3 . \cos 3x \\ f^\prime (x) & = 6\sin 3x \cos 3x \end{align*}$
$\clubsuit \, $ Menentukan limit dengan turunannya
Konsep dasar : $y=f[g(x)] \rightarrow y^\prime = f^\prime [g(x)] . g^\prime (x) $
$\begin{align*} \displaystyle \lim_{p \to 0} \frac{f(x+2p)-f(x)}{2p} & = \displaystyle \lim_{p \to 0} \frac{f^\prime (x+2p) . 2 -0}{2} \, \, \, \text{(turuna thd } \, p ) \\ & = \displaystyle \lim_{p \to 0} f^\prime (x+2p) \\ & = f^\prime (x+2.0) \\ & = f^\prime (x) \\ & = 6\sin 3x \cos 3x \end{align*}$
Jadi, nilai limitnya adalah $ 6\sin 3x \cos 3x . \heartsuit$
$\begin{align*} f(x) & =\sin ^2 3x \\ f^\prime (x) & = 2.\sin 3x . 3 . \cos 3x \\ f^\prime (x) & = 6\sin 3x \cos 3x \end{align*}$
$\clubsuit \, $ Menentukan limit dengan turunannya
Konsep dasar : $y=f[g(x)] \rightarrow y^\prime = f^\prime [g(x)] . g^\prime (x) $
$\begin{align*} \displaystyle \lim_{p \to 0} \frac{f(x+2p)-f(x)}{2p} & = \displaystyle \lim_{p \to 0} \frac{f^\prime (x+2p) . 2 -0}{2} \, \, \, \text{(turuna thd } \, p ) \\ & = \displaystyle \lim_{p \to 0} f^\prime (x+2p) \\ & = f^\prime (x+2.0) \\ & = f^\prime (x) \\ & = 6\sin 3x \cos 3x \end{align*}$
Jadi, nilai limitnya adalah $ 6\sin 3x \cos 3x . \heartsuit$
Nomor 10
$\displaystyle \lim_{x \to 1} \frac{\tan (1-x)}{x^3-1} = .... $
$\spadesuit \, $ Konsep dasar : $p^3-q^3 = (p-q)(p^2+pq+q^2) $
$x^3-1 = (x-1)(x^2+x.1+1^2) \rightarrow x^3-1 = -(1-x)(x^2+x+1)$
Konsep dasar limit :
$\displaystyle \lim_{x \to k} \frac{\tan a f(x)}{b f(x)} = \frac{a}{b} \, \, $ dengan syarat $f(k) = 0 $
$\spadesuit \, $ Menentukan limitnya
$\begin{align} \displaystyle \lim_{x \to 1} \frac{\tan (1-x)}{x^3-1} & = \displaystyle \lim_{x \to 1} \frac{\tan (1-x)}{-(1-x)(x^2+x+1)} \\ & = \displaystyle \lim_{x \to 1} \frac{\tan (1-x) }{1-x} . \frac{-1}{x^2+x+1} \\ & = \frac{1}{1} . \frac{-1}{1^2+1+1} = \frac{-1}{3} \end{align}$
Jadi, nilai limitnya adalah $ - \frac{1}{3}. \heartsuit $
$x^3-1 = (x-1)(x^2+x.1+1^2) \rightarrow x^3-1 = -(1-x)(x^2+x+1)$
Konsep dasar limit :
$\displaystyle \lim_{x \to k} \frac{\tan a f(x)}{b f(x)} = \frac{a}{b} \, \, $ dengan syarat $f(k) = 0 $
$\spadesuit \, $ Menentukan limitnya
$\begin{align} \displaystyle \lim_{x \to 1} \frac{\tan (1-x)}{x^3-1} & = \displaystyle \lim_{x \to 1} \frac{\tan (1-x)}{-(1-x)(x^2+x+1)} \\ & = \displaystyle \lim_{x \to 1} \frac{\tan (1-x) }{1-x} . \frac{-1}{x^2+x+1} \\ & = \frac{1}{1} . \frac{-1}{1^2+1+1} = \frac{-1}{3} \end{align}$
Jadi, nilai limitnya adalah $ - \frac{1}{3}. \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.