Nomor 6
Jika matriks $A = \left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right) \, \, \, $ dan $ I = \left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) \, \, $
memenuhi persamaan $A^2 = pA + qI , \, \, $ maka $ p - q = .... $
$\spadesuit \, $ Substitusi matriksnya
$\begin{align} A^2 & = pA + qI \\ \left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right).\left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right) & = p\left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right) + q\left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) \\ \left( \begin{matrix} 9 & 16 \\ 8 & 17 \end{matrix} \right) & = \left( \begin{matrix} p & 4p \\ 2p & 3p \end{matrix} \right) + \left( \begin{matrix} q & 0 \\ 0 & q \end{matrix} \right) \\ \left( \begin{matrix} 9 & 16 \\ 8 & 17 \end{matrix} \right) & = \left( \begin{matrix} p+q & 4p \\ 2p & 3p + q \end{matrix} \right) \end{align}$
$ 2p = 8 \rightarrow p = 4 $
$ p + q = 9 \rightarrow 4 + q = 9 \rightarrow q = 5 $
sehingga , $ p - q = 4 - 5 = -1 $
Jadi, nilai $ p- q = -1. \heartsuit $
$\begin{align} A^2 & = pA + qI \\ \left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right).\left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right) & = p\left( \begin{matrix} 1 & 4 \\ 2 & 3 \end{matrix} \right) + q\left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) \\ \left( \begin{matrix} 9 & 16 \\ 8 & 17 \end{matrix} \right) & = \left( \begin{matrix} p & 4p \\ 2p & 3p \end{matrix} \right) + \left( \begin{matrix} q & 0 \\ 0 & q \end{matrix} \right) \\ \left( \begin{matrix} 9 & 16 \\ 8 & 17 \end{matrix} \right) & = \left( \begin{matrix} p+q & 4p \\ 2p & 3p + q \end{matrix} \right) \end{align}$
$ 2p = 8 \rightarrow p = 4 $
$ p + q = 9 \rightarrow 4 + q = 9 \rightarrow q = 5 $
sehingga , $ p - q = 4 - 5 = -1 $
Jadi, nilai $ p- q = -1. \heartsuit $
Nomor 7
$\displaystyle \lim_{x \to \infty } \left( \sqrt{(x+p)(x+q)} - x \right) = .... $
$\clubsuit \, $ Konsep dasar
$\displaystyle \lim_{x \to \infty } \sqrt{ax^2+bx+c} - \sqrt{ax^2+mx+n} = \frac{b-m}{2\sqrt{a}} $
$\clubsuit \, $ Memodifikasi soal
$\begin{align} \displaystyle \lim_{x \to \infty } \left( \sqrt{(x+p)(x+q)} - x \right) & = \displaystyle \lim_{x \to \infty } \left( \sqrt{x^2+(p+q)x+pq} - \sqrt{x^2} \right) \\ & = \frac{b-m}{2\sqrt{a}} \\ & = \frac{(p+q)-0}{2\sqrt{1}} \\ & = \frac{1}{2} (p+q) \end{align} $
Jadi, nilai limitnya adalah $ \, \frac{1}{2} (p+q). \heartsuit$
$\displaystyle \lim_{x \to \infty } \sqrt{ax^2+bx+c} - \sqrt{ax^2+mx+n} = \frac{b-m}{2\sqrt{a}} $
$\clubsuit \, $ Memodifikasi soal
$\begin{align} \displaystyle \lim_{x \to \infty } \left( \sqrt{(x+p)(x+q)} - x \right) & = \displaystyle \lim_{x \to \infty } \left( \sqrt{x^2+(p+q)x+pq} - \sqrt{x^2} \right) \\ & = \frac{b-m}{2\sqrt{a}} \\ & = \frac{(p+q)-0}{2\sqrt{1}} \\ & = \frac{1}{2} (p+q) \end{align} $
Jadi, nilai limitnya adalah $ \, \frac{1}{2} (p+q). \heartsuit$
Nomor 8
Jika ${}^4 \log 6 = m+1 , \, \, $ maka $ {}^9 \log 8 = ..... $
$\spadesuit \, $ Sifat-sifat logaritma
${}^a \log bc = {}^a \log b + {}^a \log c , \, \, {}^a \log b = \frac{{}^p \log b }{{}^p \log a } $
$ {}^a \log b^ n = n. {}^a \log b $
$\spadesuit \, $ Menyederhanakan ${}^4 \log 6 = m+1 $
$\begin{align} {}^4 \log 6 & = m+1 \\ \frac{{}^2 \log 6 }{{}^2 \log 4 } & = m+1 \\ \frac{{}^2 \log 3 + {}^2 \log 2 }{2} & = m+1 \\ {}^2 \log 3 + 1 & = 2m + 2 \\ {}^2 \log 3 & = 2m + 1 \end{align}$
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} {}^9 \log 8 & = \frac{{}^2 \log 8 }{{}^2 \log 9 } = \frac{{}^2 \log 2^3 }{{}^2 \log 3^2 } = \frac{3.{}^2 \log 2 }{2.{}^2 \log 3 } \\ & = \frac{3.1 }{2.(2m + 1) } = \frac{3 }{4m+2} \end{align}$
Jadi, nilai $ {}^9 \log 8 = \frac{3 }{4m+2} . \heartsuit $
${}^a \log bc = {}^a \log b + {}^a \log c , \, \, {}^a \log b = \frac{{}^p \log b }{{}^p \log a } $
$ {}^a \log b^ n = n. {}^a \log b $
$\spadesuit \, $ Menyederhanakan ${}^4 \log 6 = m+1 $
$\begin{align} {}^4 \log 6 & = m+1 \\ \frac{{}^2 \log 6 }{{}^2 \log 4 } & = m+1 \\ \frac{{}^2 \log 3 + {}^2 \log 2 }{2} & = m+1 \\ {}^2 \log 3 + 1 & = 2m + 2 \\ {}^2 \log 3 & = 2m + 1 \end{align}$
$\spadesuit \, $ Menyelesaikan soal
$\begin{align} {}^9 \log 8 & = \frac{{}^2 \log 8 }{{}^2 \log 9 } = \frac{{}^2 \log 2^3 }{{}^2 \log 3^2 } = \frac{3.{}^2 \log 2 }{2.{}^2 \log 3 } \\ & = \frac{3.1 }{2.(2m + 1) } = \frac{3 }{4m+2} \end{align}$
Jadi, nilai $ {}^9 \log 8 = \frac{3 }{4m+2} . \heartsuit $
Nomor 9
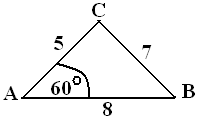
Dalam $\Delta$ ABC , AC = 5, AB = 8, dan $\angle$CAB = $60^\circ$ . Jika $\gamma = \angle BCA, \, $ maka $ \cos \gamma = .... $
$\clubsuit \, $ Gambar
$\clubsuit \, $ Aturan cosinus pada sudut A
$\begin{align*} BC^2 & = AB^2+AC^2 - 2. AB.AC . \cos A \\ & = 8^2+5^2 - 2. 8.A5 . \cos 60^\circ \\ & = 64 + 25 - 80. \frac{1}{2} \\ BC^2 & = 49 \rightarrow BC = 7 \end{align*}$
$\clubsuit \, $ Aturan cosinus pada sudut C
$\begin{align*} AB^2 & = CA^2+CB^2 - 2. CA.CB . \cos C \\ \cos C & = \frac{CA^2+CB^2-AB^2}{2.CA.CB} \\ & = \frac{5^2+7^2-8^2}{2.5.7} \\ \cos C & = \frac{1}{7} \end{align*}$
Jadi, nilai $ \cos \gamma = \frac{1}{7} . \heartsuit$

$\clubsuit \, $ Aturan cosinus pada sudut A
$\begin{align*} BC^2 & = AB^2+AC^2 - 2. AB.AC . \cos A \\ & = 8^2+5^2 - 2. 8.A5 . \cos 60^\circ \\ & = 64 + 25 - 80. \frac{1}{2} \\ BC^2 & = 49 \rightarrow BC = 7 \end{align*}$
$\clubsuit \, $ Aturan cosinus pada sudut C
$\begin{align*} AB^2 & = CA^2+CB^2 - 2. CA.CB . \cos C \\ \cos C & = \frac{CA^2+CB^2-AB^2}{2.CA.CB} \\ & = \frac{5^2+7^2-8^2}{2.5.7} \\ \cos C & = \frac{1}{7} \end{align*}$
Jadi, nilai $ \cos \gamma = \frac{1}{7} . \heartsuit$
Nomor 10
Jika $a, \, b, \, $ dan $c \, $ membentuk barisan geometri, maka $ \log a, \, \log b, \, \log c \, $ adalah ....
A. Barisan aritmetika bengan beda $ \log \frac{c}{b} $
B. Barisan aritmetika bengan beda $ \frac{c}{b} $
C. Barisan geometri dengan rasio $ \log \frac{c}{b} $
D. Barisan geometri dengan rasio $ \frac{c}{b} $
E. Bukan barisan aritmetika dan bukan barisan geometri
A. Barisan aritmetika bengan beda $ \log \frac{c}{b} $
B. Barisan aritmetika bengan beda $ \frac{c}{b} $
C. Barisan geometri dengan rasio $ \log \frac{c}{b} $
D. Barisan geometri dengan rasio $ \frac{c}{b} $
E. Bukan barisan aritmetika dan bukan barisan geometri
$\spadesuit \, $ Barisan geometri : $a, \, b, \, $ dan $c \, $
Rasio sama : $ r = \frac{b}{a} = \frac{c}{b} $
Cek barisan $ \log a, \, \log b, \, \log c \, $
$\spadesuit \, $ apakah barisan aritmetika ?
Selisih sama :
$S_1 = \log b - \log a = \log \frac{b}{a} = \log r $
$S_2 = \log c - \log b = \log \frac{c}{b} = \log r $
sehingga $ S_1 = S_2 \, \, $ (selisis dua suku sama)
karena selisihnya sama, maka barisan terebut termasuk barisan aritmetika.
$\spadesuit \, $ apakah barisan geometri ?
Rasio sama :
$R_1 = \frac{\log b}{\log a} = {}^a \log b $
$R_2 = \frac{\log c}{\log b} = {}^b \log $
sehingga $ R_1 \neq R_2 \, \, $ (Rasio dua suku tidak sama)
karena rasio tidak sama, maka barisan terebut bukan barisan geometri.
Jadi, $ \log a, \, \log b, \, \log c \, \, $ adalah barisan aritmetika dengan beda $ \log \frac{c}{b} . \heartsuit $
Rasio sama : $ r = \frac{b}{a} = \frac{c}{b} $
Cek barisan $ \log a, \, \log b, \, \log c \, $
$\spadesuit \, $ apakah barisan aritmetika ?
Selisih sama :
$S_1 = \log b - \log a = \log \frac{b}{a} = \log r $
$S_2 = \log c - \log b = \log \frac{c}{b} = \log r $
sehingga $ S_1 = S_2 \, \, $ (selisis dua suku sama)
karena selisihnya sama, maka barisan terebut termasuk barisan aritmetika.
$\spadesuit \, $ apakah barisan geometri ?
Rasio sama :
$R_1 = \frac{\log b}{\log a} = {}^a \log b $
$R_2 = \frac{\log c}{\log b} = {}^b \log $
sehingga $ R_1 \neq R_2 \, \, $ (Rasio dua suku tidak sama)
karena rasio tidak sama, maka barisan terebut bukan barisan geometri.
Jadi, $ \log a, \, \log b, \, \log c \, \, $ adalah barisan aritmetika dengan beda $ \log \frac{c}{b} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.