Nomor 1
Nilai dari : $(\sqrt{2}+\sqrt{3}+2+\sqrt{5})(-\sqrt{2}+\sqrt{3}+2-\sqrt{5})(\sqrt{10}+2\sqrt{3})= .... $
$\clubsuit \, $ Konsep Dasar : $(p+q)(p-q)=p^2-q^2$
$\begin{align} & (\sqrt{2}+\sqrt{3}+2+\sqrt{5})(-\sqrt{2}+\sqrt{3}+2-\sqrt{5}) \\ & = ([2+\sqrt{3}]+[\sqrt{2}+\sqrt{5}])([2+\sqrt{3}]-[\sqrt{2}+\sqrt{5}]) \\ & = (2+\sqrt{3})^2 - (\sqrt{2}+\sqrt{5})^2 \\ & = (4+4\sqrt{3}+3) - (2+2\sqrt{10}+5) \\ & = 4\sqrt{3} - 2\sqrt{10} \\ & = 2(2\sqrt{3} - \sqrt{10}) \end{align}$
$\clubsuit \, $ Menyelesaikan soal
$\begin{align} & (\sqrt{2}+\sqrt{3}+2+\sqrt{5})(-\sqrt{2}+\sqrt{3}+2-\sqrt{5})(\sqrt{10}+2\sqrt{3}) \\ & = 2(2\sqrt{3} - \sqrt{10})(2\sqrt{3}+\sqrt{10}) \\ & = 2 [(2\sqrt{3})^2 - (\sqrt{10})^2 ] \\ & = 2[12-10] \\ & = 2.2 = 4 \end{align}$
Jadi, hasilnya adalah 4. $ \heartsuit $
$\begin{align} & (\sqrt{2}+\sqrt{3}+2+\sqrt{5})(-\sqrt{2}+\sqrt{3}+2-\sqrt{5}) \\ & = ([2+\sqrt{3}]+[\sqrt{2}+\sqrt{5}])([2+\sqrt{3}]-[\sqrt{2}+\sqrt{5}]) \\ & = (2+\sqrt{3})^2 - (\sqrt{2}+\sqrt{5})^2 \\ & = (4+4\sqrt{3}+3) - (2+2\sqrt{10}+5) \\ & = 4\sqrt{3} - 2\sqrt{10} \\ & = 2(2\sqrt{3} - \sqrt{10}) \end{align}$
$\clubsuit \, $ Menyelesaikan soal
$\begin{align} & (\sqrt{2}+\sqrt{3}+2+\sqrt{5})(-\sqrt{2}+\sqrt{3}+2-\sqrt{5})(\sqrt{10}+2\sqrt{3}) \\ & = 2(2\sqrt{3} - \sqrt{10})(2\sqrt{3}+\sqrt{10}) \\ & = 2 [(2\sqrt{3})^2 - (\sqrt{10})^2 ] \\ & = 2[12-10] \\ & = 2.2 = 4 \end{align}$
Jadi, hasilnya adalah 4. $ \heartsuit $
Nomor 2
Grafik hasil produksi suatu pabrik per tahun merupakan suatu garis lurus. Jika produksi pada tahun pertama 110 unit dan pada
tahun ketiga 150 unit, maka produksi tahun ke-15 adalah ....
$\spadesuit \, $ Menentukan persamaan garis yang melalui titik
$(x_1,y_1) = (1, \, 110) \, \, $ dan $ \, \, (x_2,y_2) = (3, \, 150) $
$\begin{align} \frac{y-y_1}{y_2-y_1} & = \frac{x-x_1}{x_2-x_1} \\ \frac{y-110}{150-110} & = \frac{x-1}{3-1} \\ \frac{y-110}{40} & = \frac{x-1}{2} \\ 2(y-110) & = 40(x-1) \\ y-110 & = 20(x-1) \\ y & = 20x + 90 \end{align}$
Sehingga pada tahun ke-15, artinya $ \, x = 15 $
$y = 20x + 90 \rightarrow y= 20. 15 + 90 = 300 + 90 = 390 $
Jadi, produksi tahun ke-15 adalah 390. $ \heartsuit $
$(x_1,y_1) = (1, \, 110) \, \, $ dan $ \, \, (x_2,y_2) = (3, \, 150) $
$\begin{align} \frac{y-y_1}{y_2-y_1} & = \frac{x-x_1}{x_2-x_1} \\ \frac{y-110}{150-110} & = \frac{x-1}{3-1} \\ \frac{y-110}{40} & = \frac{x-1}{2} \\ 2(y-110) & = 40(x-1) \\ y-110 & = 20(x-1) \\ y & = 20x + 90 \end{align}$
Sehingga pada tahun ke-15, artinya $ \, x = 15 $
$y = 20x + 90 \rightarrow y= 20. 15 + 90 = 300 + 90 = 390 $
Jadi, produksi tahun ke-15 adalah 390. $ \heartsuit $
Cara II
$\spadesuit \, $ Karena berbentuk garis lurus, maka kenaikannya akan sama sehingga bisa dianggap sebagai barisan aritmetika
$\spadesuit \, $ Barisan aritmetika : $U_n = a+(n-1)b $
tahun ke-1 $ \, \rightarrow U_1 = a = 110 $
tahun ke-3 $ \, \rightarrow U_3 = 150 $
$ U_3 = 150 \rightarrow a+2b = 150 \rightarrow 110 + 2b = 150 \rightarrow b = 20 $
Sehingga tahun ke-15
$ U_{15} = a+14b = 110 + 14. 20 = 110 + 280 = 390 $
Jadi, produksi tahun ke-15 adalah 390. $ \heartsuit $
$\spadesuit \, $ Karena berbentuk garis lurus, maka kenaikannya akan sama sehingga bisa dianggap sebagai barisan aritmetika
$\spadesuit \, $ Barisan aritmetika : $U_n = a+(n-1)b $
tahun ke-1 $ \, \rightarrow U_1 = a = 110 $
tahun ke-3 $ \, \rightarrow U_3 = 150 $
$ U_3 = 150 \rightarrow a+2b = 150 \rightarrow 110 + 2b = 150 \rightarrow b = 20 $
Sehingga tahun ke-15
$ U_{15} = a+14b = 110 + 14. 20 = 110 + 280 = 390 $
Jadi, produksi tahun ke-15 adalah 390. $ \heartsuit $
Nomor 3
Jika $a=\frac{1-\sqrt{3}}{1+\sqrt{3}} \, \, $ dan $ b = \frac{1+\sqrt{3}}{1-\sqrt{3}}, \, \, $ maka $ a + b = .... $
$\clubsuit \, $ Jumlahkan dan samakan penyebutnya
$\begin{align*} a+ b & = \frac{1-\sqrt{3}}{1+\sqrt{3}} + \frac{1+\sqrt{3}}{1-\sqrt{3}} \\ & = \frac{(1-\sqrt{3})(1-\sqrt{3}) + (1+\sqrt{3})(1+\sqrt{3})}{(1+\sqrt{3})(1-\sqrt{3})} \\ & = \frac{(1-2\sqrt{3}+3) + (1+2\sqrt{3}+3)}{1-3} \\ & = \frac{8}{-2} = -4 \end{align*}$
Jadi, hasilnya adalah -4. $ \heartsuit $
$\begin{align*} a+ b & = \frac{1-\sqrt{3}}{1+\sqrt{3}} + \frac{1+\sqrt{3}}{1-\sqrt{3}} \\ & = \frac{(1-\sqrt{3})(1-\sqrt{3}) + (1+\sqrt{3})(1+\sqrt{3})}{(1+\sqrt{3})(1-\sqrt{3})} \\ & = \frac{(1-2\sqrt{3}+3) + (1+2\sqrt{3}+3)}{1-3} \\ & = \frac{8}{-2} = -4 \end{align*}$
Jadi, hasilnya adalah -4. $ \heartsuit $
Nomor 4
Garis $h \, $ memotong sumbu X positif di A dan sumbu Y positif di B. Jika O adalah titik pangkal sistem koordinat,
OA = 3, dan OB = 4, maka persamaan garis $g \, $ yang melalui O dan tegak lurus pada $h \, $ adalah ....
$\spadesuit \, $ Gambar
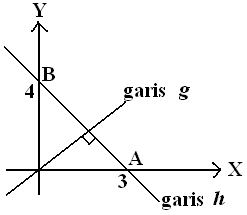
$\spadesuit \, $ Gradien garis $h$
$m_h = \frac{-y}{x} = \frac{-4}{3} $
$\spadesuit \, $ Garis $g \, $ tegak lurus garis $\, h $
$m_g.m_h = -1 \rightarrow m_g = \frac{-1}{m_h} = \frac{-1}{\frac{-4}{3}} = \frac{3}{4} $
$\spadesuit \, $ Persamaan garis $g \, $ melalui titik (0,0) dengan gradien $ \frac{3}{4} $
$\begin{align} y-y_1 & = m(x-x_1) \\ y- 0 & = \frac{3}{4}.(x-0) \\ y & = \frac{3}{4}x \end{align}$
Jadi, persamaan garis $g \, $ adalah $ y = \frac{3}{4}x . \heartsuit $

$\spadesuit \, $ Gradien garis $h$
$m_h = \frac{-y}{x} = \frac{-4}{3} $
$\spadesuit \, $ Garis $g \, $ tegak lurus garis $\, h $
$m_g.m_h = -1 \rightarrow m_g = \frac{-1}{m_h} = \frac{-1}{\frac{-4}{3}} = \frac{3}{4} $
$\spadesuit \, $ Persamaan garis $g \, $ melalui titik (0,0) dengan gradien $ \frac{3}{4} $
$\begin{align} y-y_1 & = m(x-x_1) \\ y- 0 & = \frac{3}{4}.(x-0) \\ y & = \frac{3}{4}x \end{align}$
Jadi, persamaan garis $g \, $ adalah $ y = \frac{3}{4}x . \heartsuit $
Nomor 5
Jika $ \sin \theta = - \frac{1}{4} \, \, $ dan $ \tan \theta > 0 , \, \, $ maka $ \cos \theta = ....$
$\clubsuit \, $ Karena $\sin \theta \, $ negatif dan $\tan \theta \, $ positif, maka $ \theta \, $ di kuadran III
sehingga nilai $\cos \theta \, $ juga negatif
$\clubsuit \, $ Buat segitiga
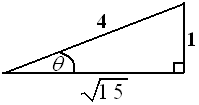
sehingga, $\cos \theta = - \frac{\sqrt{15}}{4} $
Jadi, nilai $ \cos \theta = - \frac{\sqrt{15}}{4} . \heartsuit$
$\clubsuit \, $ Buat segitiga

sehingga, $\cos \theta = - \frac{\sqrt{15}}{4} $
Jadi, nilai $ \cos \theta = - \frac{\sqrt{15}}{4} . \heartsuit$
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.