Nomor 6
Diketahui kubus ABCD.EFGH dengan panjang rusuknya $ 2 a $ . Jika P titik tengah BF dan Q titik tengah EH, maka panjang PQ = ....
$\spadesuit \, $ Gambar
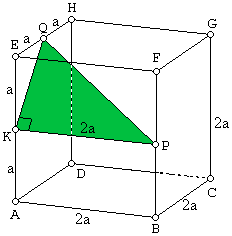
Segitiga KEQ , $ KQ = \sqrt{KE^2+ EQ^2} = \sqrt{a^2+a^2} = a\sqrt{2} $
$\spadesuit \, $ Menentukan panjang PQ
$\begin{align} PQ & = \sqrt{PK^2 + KQ^2} \\ & = \sqrt{(2a)^2 + (a\sqrt{2})^2} \\ & = \sqrt{4a^2 + 2a^2} \\ & = a\sqrt{6} \end{align}$
Jadi, panjang $ PQ = a\sqrt{6} . \heartsuit $

Segitiga KEQ , $ KQ = \sqrt{KE^2+ EQ^2} = \sqrt{a^2+a^2} = a\sqrt{2} $
$\spadesuit \, $ Menentukan panjang PQ
$\begin{align} PQ & = \sqrt{PK^2 + KQ^2} \\ & = \sqrt{(2a)^2 + (a\sqrt{2})^2} \\ & = \sqrt{4a^2 + 2a^2} \\ & = a\sqrt{6} \end{align}$
Jadi, panjang $ PQ = a\sqrt{6} . \heartsuit $
Nomor 7
Jika $ 3^{x+2} + 9^{x+1} = 810 , \, $ maka $ 3^{x-3} = ..... $
$\clubsuit \, $ Sifat eksponen
$a^{m+n} = a^m.a^n , \, \, a^{m-n} = \frac{a^m}{a^n}, \, a^{-n} = \frac{1}{a^n} , \, $
dan $ \, (a^m)^n = a^{mn} $
$\clubsuit \, $ Menyelesaikan persamaan dengan $ \, p = 3^x \, $ (positif)
$\begin{align} 3^{x+2} + 9^{x+1} & = 810 \\ 3^x.3^2 + 9^x . 9^1 - 810 & = 0 \\ 9.3^x + 9.(3^2)^x - 810 & = 0 \\ 9.3^x + 9.(3^x)^2 - 810 & = 0 \, \, \, \text{(bagi 9)} \\ 3^x + (3^x)^2 - 90 & = 0 \, \, \, \text{(substitusi } \, p = 3^x ) \\ p + p^2 - 90 & = 0 \\ (p-9)(p+10) & = 0 \\ p=9 \vee p & = -10 \\ p=9 \rightarrow 3^x & = 9 \rightarrow x = 2 \\ p=-10 \rightarrow & \, \text{(tidak memenuhi)} \end{align}$
Sehingga nilai : $ 3^{x-3} = 3^{2-3} = 3^{-1} = \frac{1}{3^1} = \frac{1}{3} $
Jadi, nilai $ 3^{x-3} = \frac{1}{3} . \heartsuit$
$a^{m+n} = a^m.a^n , \, \, a^{m-n} = \frac{a^m}{a^n}, \, a^{-n} = \frac{1}{a^n} , \, $
dan $ \, (a^m)^n = a^{mn} $
$\clubsuit \, $ Menyelesaikan persamaan dengan $ \, p = 3^x \, $ (positif)
$\begin{align} 3^{x+2} + 9^{x+1} & = 810 \\ 3^x.3^2 + 9^x . 9^1 - 810 & = 0 \\ 9.3^x + 9.(3^2)^x - 810 & = 0 \\ 9.3^x + 9.(3^x)^2 - 810 & = 0 \, \, \, \text{(bagi 9)} \\ 3^x + (3^x)^2 - 90 & = 0 \, \, \, \text{(substitusi } \, p = 3^x ) \\ p + p^2 - 90 & = 0 \\ (p-9)(p+10) & = 0 \\ p=9 \vee p & = -10 \\ p=9 \rightarrow 3^x & = 9 \rightarrow x = 2 \\ p=-10 \rightarrow & \, \text{(tidak memenuhi)} \end{align}$
Sehingga nilai : $ 3^{x-3} = 3^{2-3} = 3^{-1} = \frac{1}{3^1} = \frac{1}{3} $
Jadi, nilai $ 3^{x-3} = \frac{1}{3} . \heartsuit$
Nomor 8
Jika gambar di bawah ini adalah grafik $ y = \frac{df(x)}{dx} \, $
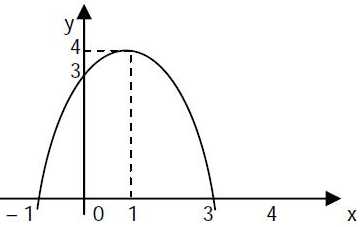
Maka dapat disimpulkan bahwa fungsi $ f(x) $ .....
A. mencapai nilai maksimum di $ x = 1 $
B. mencapai nilai minimum di $ x = -1 $
C. naik pada interval $ \{x | x < 1 \} $
D. selalu memotong sumbu Y di titik (0,3)
E. merupakan fungsi kuadrat

Maka dapat disimpulkan bahwa fungsi $ f(x) $ .....
A. mencapai nilai maksimum di $ x = 1 $
B. mencapai nilai minimum di $ x = -1 $
C. naik pada interval $ \{x | x < 1 \} $
D. selalu memotong sumbu Y di titik (0,3)
E. merupakan fungsi kuadrat
$\spadesuit \, $ Gambar adalah grafik $ y = \frac{df(x)}{dx} \, $ atau $ y = f^\prime (x), \, $
artinya grafik di atas adalah grafik turunan pertamanya.
$\spadesuit \, $ Konsep dasar turunan pertama
Syarat stasioner (nilai max/min) : $ f^\prime (x) = 0 $
interval naik : $ f^\prime (x) > 0 $
interval turun : $ f^\prime (x) < 0 $
$\spadesuit \, $ Analisa grafik turunannya
*). Titik potong sumbu X nya saat $ f^\prime (x) = 0 $ adalah $ x = -1 $ dan $ x = 3 $ , artinya stasionernya (nilai maksimum atau minimum) saat $ x = -1 $ dan $ x = 3 $ .
*). Untuk $ x < -1 \, $ grafik ada di bawah sumbu X artinya $ f^\prime (x) < 0 \, $ (nilai turunannya negatif), untuk $ -1 < x < 3 \, $ nilai $ f^\prime (x) > 0 \, $ dan $ x > 3 \, $ nilai $ f^\prime (x) < 0 $
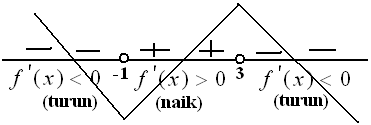
artinya fungsi $ f(x) $ maksimum saat $ x = 3 \, $ dan minimum saat $ x = -1 $
Jadi, fungsi $ f(x) \, $ mencapai minimum di $ x = -1. \heartsuit$
$\spadesuit \, $ Konsep dasar turunan pertama
Syarat stasioner (nilai max/min) : $ f^\prime (x) = 0 $
interval naik : $ f^\prime (x) > 0 $
interval turun : $ f^\prime (x) < 0 $
$\spadesuit \, $ Analisa grafik turunannya
*). Titik potong sumbu X nya saat $ f^\prime (x) = 0 $ adalah $ x = -1 $ dan $ x = 3 $ , artinya stasionernya (nilai maksimum atau minimum) saat $ x = -1 $ dan $ x = 3 $ .
*). Untuk $ x < -1 \, $ grafik ada di bawah sumbu X artinya $ f^\prime (x) < 0 \, $ (nilai turunannya negatif), untuk $ -1 < x < 3 \, $ nilai $ f^\prime (x) > 0 \, $ dan $ x > 3 \, $ nilai $ f^\prime (x) < 0 $
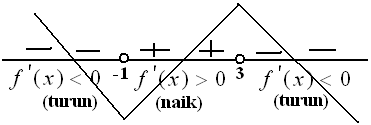
artinya fungsi $ f(x) $ maksimum saat $ x = 3 \, $ dan minimum saat $ x = -1 $
Jadi, fungsi $ f(x) \, $ mencapai minimum di $ x = -1. \heartsuit$
Nomor 9
Diketahui salah satu asimtot dari $ \frac{x^2}{4} - \frac{f^2}{b^2} = 1 \, $ sejajar dengan garis $ 6x - 3y + 5 = 0, \, $
maka $ b^2 = .... $
$\clubsuit \, $ Konsep dasar Hiperbola
$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $
Persamaan asimtotnya : $ y = \frac{b}{a}x \, $ dan $ \, y = -\frac{b}{a}x $
$\clubsuit \, $ Hiperbola $ \frac{x^2}{4} - \frac{f^2}{b^2} = 1 \, $ sama dengan $ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \, $
Memiliki asimtot :
$ y = \frac{b}{a}x \rightarrow y = \frac{b}{2}x \rightarrow m_1 = \frac{b}{2} $
$ y = -\frac{b}{a}x \rightarrow y = -\frac{b}{2}x \rightarrow m_1 = -\frac{b}{2} $
$\clubsuit \, $ Gradien garis : $ 6x - 3y + 5 = 0 $
$ m = \frac{-x}{y} = \frac{-6}{-3} = 2 $
$\clubsuit \, $ Gradien garis positif, dan asimtot sama dengan gradien garis, sehingga gradien salah satu asimtot sama dengan gradien garis. Karena gradiennya positif, maka garis naik, dan asimtot yang gradiennya positif adalah $ y = \frac{b}{2}x \rightarrow m_1 = \frac{b}{2} $
Gradien sama : $ m_1 = m \rightarrow \frac{b}{2} = 2 \rightarrow b = 4 $
Sehingga nilai $ b^2 = 4^2 = 16 $
Jadi, nilai $ b^2 = 16 . \heartsuit $
Persamaan asimtotnya : $ y = \frac{b}{a}x \, $ dan $ \, y = -\frac{b}{a}x $
$\clubsuit \, $ Hiperbola $ \frac{x^2}{4} - \frac{f^2}{b^2} = 1 \, $ sama dengan $ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \, $
Memiliki asimtot :
$ y = \frac{b}{a}x \rightarrow y = \frac{b}{2}x \rightarrow m_1 = \frac{b}{2} $
$ y = -\frac{b}{a}x \rightarrow y = -\frac{b}{2}x \rightarrow m_1 = -\frac{b}{2} $
$\clubsuit \, $ Gradien garis : $ 6x - 3y + 5 = 0 $
$ m = \frac{-x}{y} = \frac{-6}{-3} = 2 $
$\clubsuit \, $ Gradien garis positif, dan asimtot sama dengan gradien garis, sehingga gradien salah satu asimtot sama dengan gradien garis. Karena gradiennya positif, maka garis naik, dan asimtot yang gradiennya positif adalah $ y = \frac{b}{2}x \rightarrow m_1 = \frac{b}{2} $
Gradien sama : $ m_1 = m \rightarrow \frac{b}{2} = 2 \rightarrow b = 4 $
Sehingga nilai $ b^2 = 4^2 = 16 $
Jadi, nilai $ b^2 = 16 . \heartsuit $
Nomor 10
Fungsi $ f(x) = (a+4)x^2 - ax\sqrt{2} + ( a-3) \, $ bernilai tak negatif jika ....
$\spadesuit \, $ Fungsi $ f(x) $ tak negatif, artinya selalu positif (definit positif)
Syarat Definit positif : $ a > 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Fungsi $ f(x) = (k+4)x^2 - kx\sqrt{2} + ( k-3) \, $
$ a = k+4 , \, b = -k\sqrt{2}, \, c = k - 3 $
$\spadesuit \, $ Menyelesaikan syarat definit positif
*). $ a > 0 \rightarrow k+4 > 0 \rightarrow k > -4 \, $ ...(HP1)
*). Karena tak negatif, berarti nol boleh ikut ($D \leq 0 $)
$\begin{align} D & \leq 0 \\ b^2 - 4ac & \leq 0 \\ (-k\sqrt{2})^2 - 4(k+4)(k-3) & \leq 0 \\ 2k^2 - 4k^2 - 4k + 48 & \leq 0 \\ -2k^2 - 4k + 48 & \leq 0 \, \, \text{(bagi -2, tanda dibalik)} \\ k^2 + 2k - 24 & \geq 0 \\ (k-4)(k+6) & = 0 \\ k = 4 \vee k & = -6 \end{align}$
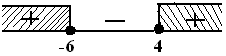
HP2 = $ \{ k \leq -6 \vee k \geq 4 \} $
Sehingga solusinya : HP = $ HP1 \cap HP2 = \{ k \geq 4 \} $
Jadi, solusinya $ HP = \{ k \geq 4 \} . \heartsuit $
Syarat Definit positif : $ a > 0 \, $ dan $ D < 0 $
$\spadesuit \, $ Fungsi $ f(x) = (k+4)x^2 - kx\sqrt{2} + ( k-3) \, $
$ a = k+4 , \, b = -k\sqrt{2}, \, c = k - 3 $
$\spadesuit \, $ Menyelesaikan syarat definit positif
*). $ a > 0 \rightarrow k+4 > 0 \rightarrow k > -4 \, $ ...(HP1)
*). Karena tak negatif, berarti nol boleh ikut ($D \leq 0 $)
$\begin{align} D & \leq 0 \\ b^2 - 4ac & \leq 0 \\ (-k\sqrt{2})^2 - 4(k+4)(k-3) & \leq 0 \\ 2k^2 - 4k^2 - 4k + 48 & \leq 0 \\ -2k^2 - 4k + 48 & \leq 0 \, \, \text{(bagi -2, tanda dibalik)} \\ k^2 + 2k - 24 & \geq 0 \\ (k-4)(k+6) & = 0 \\ k = 4 \vee k & = -6 \end{align}$
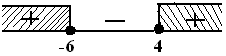
HP2 = $ \{ k \leq -6 \vee k \geq 4 \} $
Sehingga solusinya : HP = $ HP1 \cap HP2 = \{ k \geq 4 \} $
Jadi, solusinya $ HP = \{ k \geq 4 \} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.